Proto-RL
Contents
Proto-RL#
제목: Reinforcement Learning with Prototypical Representations
저자: Yarats, Denis, Rob Fergus, Alessandro Lazaric, and Lerrel Pinto
연도: 2021년
학술대회: ICML
키워드: Unsupervised RL, Exploration
현재 이미지 상태공간에서 off-policy model-free 알고리즘 중 SOTA 알고리즘인 DrQ-v2의 논문을 읽고 난 후 논문의 저자인 Denis Yarats의 팬이 되어버렸다.
굵직 굵직한 논문을 많이 쓴 것은 둘째 치고, 코드를 정말 쉽고 간결하게 핵심 기능만 작성하는 저자의 코딩 스타일이 너무나도 마음에 들었기 때문이다.
요 근래 Denis Yarats의 논문 몇 편을 읽으면서 그 중 재밌었던 Proto-RL을 기록용으로 짧게 정리하려고 한다.
이미지 상태공간에서 가장 중요한 것은 뭐니 뭐니 해도 입력 이미지를 저차원 latent vector로 잘 임베딩할 수 있는 encoder를 훈련시키는 것일 것이다. 이 embedding vector는 입력 이미지에서 문제를 해결하는 데 필요한 정보를 표현 (representation)할 수 있어야 할 것이다. 하지만 강화학습에서 representation learning이 어려운 이유가 있다.
좋은 representation을 얻기 위해서는 다양한 데이터로부터 학습해야 한다. 다양한 데이터를 수집하기 위해서는 탐색 (exploration)을 해야 한다.
좋은 탐색을 하기 위해서는 내가 방문한 상태가 예전에 방문했던 상태들과 얼마나 다른지 측정해야 한다. 이 측정 과정은 계산 복잡도상 latent space에서 진행되기 때문에 상태들에 대한 좋은 representation이 필요하다.
즉, 닭이 먼저냐 달걀이 먼저냐의 싸움이 된다. 이와 같은 문제로 task reward를 통해 에이전트를 학습하는 일반적인 강화학습 알고리즘에 representation learning을 추가하는 것만으로는 좋은 representation이 학습되지 않는다. 따라서 Proto-RL은 task reward를 사용하지 않고, intrisic reward를 통해 환경을 탐험하며 데이터를 수집하고 encoder를 포함한 네트워크들을 학습시킨다. 이 과정을 task-agnostic exploration이라고 부른다. 이렇게 unsupervised RL을 통해 사전학습된 네트워크들은 이후에 task reward와 instrisic reward를 모두 최대화하도록 미세조정되어 task를 해결하게 된다.
예컨대, 첫 50만 번의 상호작용 동안에는 task-agnostic exploration을 통해 unsupervised RL을 진행하고, 이후 50만 번 동안 task reward와 intrinsic reward를 모두 사용하여 에이전트를 학습시킬 경우, 처음부터 백만 번 task reward (optionally, instrisic reward도 포함)를 사용하여 학습했을 때보다 성능이 더 좋게 나온다:
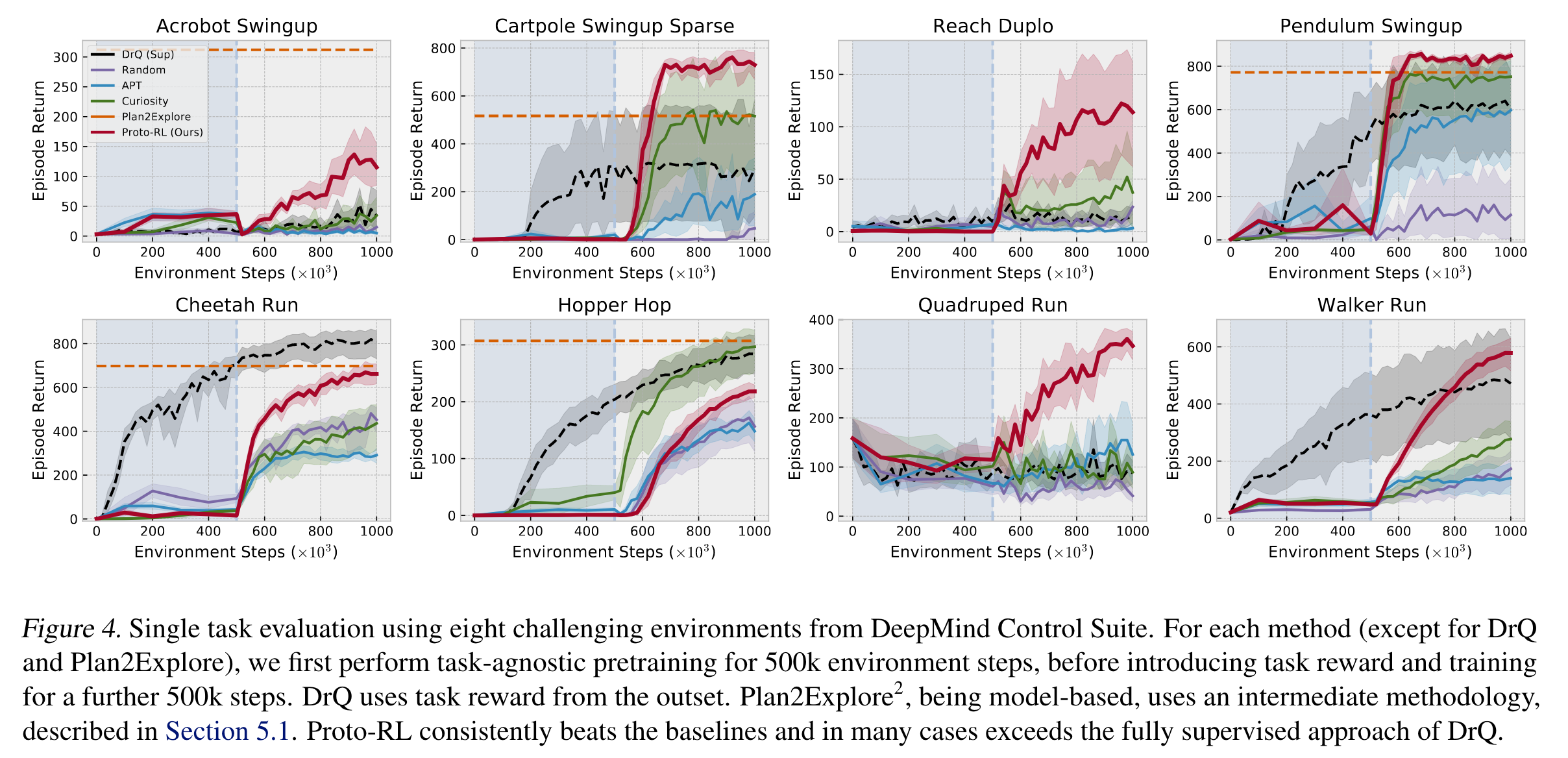
위 그림에서 검은색 점선으로 나타나는 DrQ는 처음부터 task reward를 사용하여 네트워크를 학습시키는 알고리즘이다. 참고로 DrQ는 representation learning을 따로 포함하지 않는 알고리즘이다. 빨간색 선이 Proto-RL의 학습 곡선을 나타내며 첫 50만 번은 task reward를 최대화하지 않고 unsupervised RL을 통해 네트워크를 학습시킨다. 이후 50만 번의 상호작용만으로 DrQ 성능을 뛰어 넘는 것을 확인할 수 있다.
Prototypical representation learning#
Proto-RL의 representation learning에는 contrastive learning (CL)이 사용된다. 참고로 일반적인 CL 방법론들은 다음과 같은 과정을 수행한다.
현재 샘플 \(x\)에 대해서 positive 샘플 \(x^+\)와 negative 샘플 \(x^-\)을 정의한다.
Positive 샘플은 주로 현재 샘플 \(x\)에 data augmentation 기법이 적용된 샘플 \(\text{aug}(x)\)으로 정의된다.
미니 배치 내 \(x\)를 제외한 다른 나머지 샘플들이 negative 샘플이 된다.
다음으로 현재 샘플과 positive/negative 샘플의 임베딩 벡터를 각각 \(z, z^{+}, z^{-}\)라고 할 때, \(z\)와 \(z^{+}\)의 유사도는 최대화하고, \(z\)와 \(z^{-}\)의 유사도는 최소화 한다.
Proto-RL은 CL 방법론 중 SwAV이란 방법론의 아이디어를 채용한다. 샘플과 샘플을 비교하는 일반적인 CL과 다르게 Proto-RL에서는 현재 샘플이 \(M\)개의 군집 중 어느 군집에 속할지에 대한 확률과 positive 샘플이 어떤 군집에 속해 있는지를 일치시켜주게 학습이 된다. 그러기 위해선 latent space \(M\)개의 군집 역할을 하는 vectors \(\left\{ \mathbf{c}_i \right\}_{i=1}^{M}\)들을 prototype vectors라고 부른다. 참고로 실험에서는 \(M=512\)를 사용하며 latent space의 차원은 \(128\)차원이다. 논문에서 제안하는 prototypical representation learning은 아래 그림처럼 진행된다.
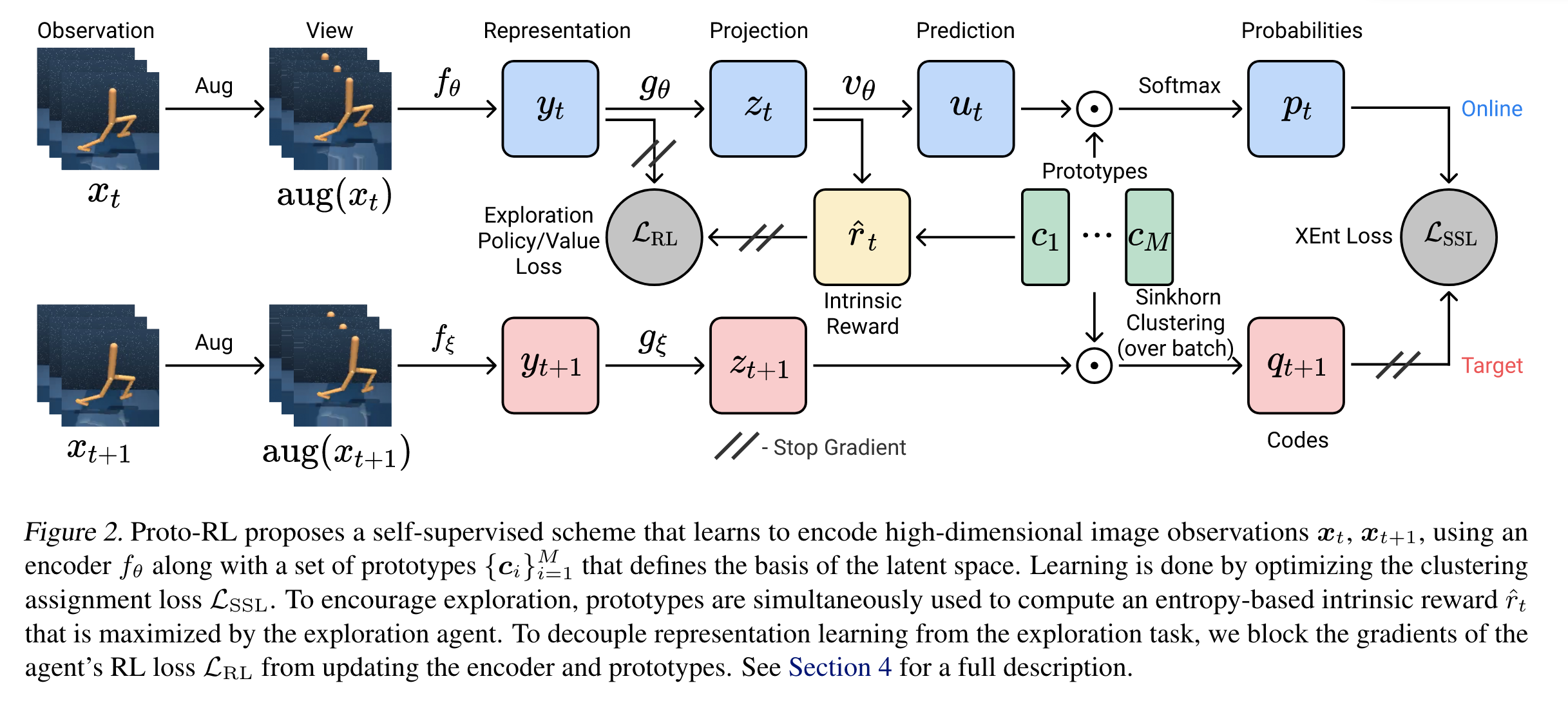
우선 그림에서 observation 벡터 \(\mathbf{x}_t\)는 최근 \(3\)개의 frames를 stack하여 \(9\times 84 \times 94\) 사이즈를 갖는다. 현재 observation \(\mathbf{x}_t\)의 positive 샘플로는 다음 observation \(x_{t+1}\)이 설정된다.
현재 observation \(\mathbf{x}_t\)은 다음과 같은 과정을 지나게 된다.
\(\mathbf{x}_t\)에 먼저 간단한 random shift augmentation이 적용된 후 encoder \(f_{\theta}\)를 지나 representation vector \(\mathbf{y}_t\)가 된다. Representation vector는 \(39200\)차원 벡터이다.
Representation vector \(\mathbf{y}_t\)는 \(39200\)차원 벡터를 \(128\)차원으로 변환시켜주는 linear layer \(g_{\theta}\)를 지나 latent vector \(\mathbf{z}_t\)가 된다.
Latent vector \(\mathbf{z}_t\)는 2층짜리 MLP prediction 네트워크 \(v_{\theta}\)를 지나 prediction \(\mathbf{u}_t\)가 된다. Prediction 역시 \(128\)차원이다.
Prediction \(\mathbf{u}_t\)가 각 prototypes \(\mathbf{c}_i\)에 속할 확률을 다음과 같이 계산한다. 유사도를 기반으로 하여 확률을 부여한 것이다.
\(i=1, \ldots, M\)에 대해서 확률값 \(p_t^{(i)}\)을 원소로 갖는 벡터 \(\mathbf{p}_t\)를 probability vector라고 부른다.
Positive 샘플인 다음 observation \(\mathbf{x}_{t+1}\)도 유사한 과정을 지나게 된다. 단, 여기서 네트워크들은 모두 target network로서 역전파를 통해 학습되지는 않는다. 이를 나타내기 위하여 그림에서 네트워크 파라미터가 \(\xi\)로 표기되어 있다. 파라미터 \(\xi\)는 soft target update와 동일하게 online 파라미터 \(\theta\)의 exponential moving average로 업데이트된다.
\(\mathbf{x}_{t+1} \rightarrow \mathbf{y}_{t+1} \rightarrow \mathbf{z}_{t+1}\)으로 변환되는 과정은 동일하다.
다음으로 latent vector \(\mathbf{z}_{t+1}\)가 어느 prototypes에 속할지 확률을 계산하게 되는데, 이때 Sinkhorn-Knopp 클러스터링 알고리즘이 사용된다고 한다. 이 알고리즘에 대한 정리는 나중에 추가하도록 하겠다.
확률값들을 담은 target probability 벡터를 \(\mathbf{q}_{t+1}\)이라고 하자.
Proto-RL에서는 probability vector \(\mathbf{p}_i\)와 target probability vector \(\mathbf{q}_{t+1}\)의 cross-entropy loss를 CL의 목적함수로 설정하였다.
이때, target probability vector \(\mathbf{q}_{t+1}\)은 타겟값으로 사용되는 것이기 때문에 상수 취급을 해줘야 한다. 이는 위 그림에서 빗금으로 표시된 stop-gradient를 통해 처리된다.
가만보면 \(\mathbf{x}_t\)을 probability vector \(\mathbf{p}_t\)로 만들어주는 과정과 \(\mathbf{x}_{t+1}\)을 probability vector \(\mathbf{q}_{t+1}\)로 만들어주는 과정이 대칭적이지 않다. \(\mathbf{p}_t\)를 만들 때는 latent vector \(\mathbf{z}_t\)에서 prediction 네트워크를 통과한 prediction vector \(\mathbf{u}_t\)에 대해 prototypes에 속할 확률을 계산한다. 이렇게 비대칭적인 구조를 택한 이유는 네트워크들이 trivial soltions로 수렴하는 collapse를 방지하기 위함이라고 한다.
Maximum entropy exploration#
지금까지 데이터가 수집되었다는 가정 하에 CL을 어떻게 할지에 대해 알아보았다. 다음으로 탐험을 통해 다양한 데이터를 수집하도록 에이전트를 훈련시키는 방법에 대해 알아보자. Task reward를 사용하지 않는 unsupervised RL 특성상 새롭게 보상 함수를 정의해야 한다. 환경에서 정의된 reward가 아닌 강화학습 알고리즘이 고유하게 정의하는 보상 함수이기 때문에 intrinsic reward라고 부른다. 이후에는 정의한 intrinsic reward에 SAC 등 일반적인 강화학습 알고리즘을 적용하여 정책을 훈련시키며 데이터를 수집하면 된다.
에이전트가 최대한 많은 상태를 탐험하는 것을 목표로 하기 때문에 정책을 따랐을 때 가능한 많은 상태들을 골고루 방문하면 좋을 것이다. 따라서 정책을 따랐을 때 상태들에 방문할 확률분포 \(d^{\pi}(\cdot)\)의 엔트로피를 intrinsic reward를 사용한다. 먼저 주어진 정책 \(\pi\)의 discounted state visitation distribution \(d^{\pi}(\mathbf{x})\)는 다음과 같이 정의된다.
이때, \(d^{\pi}_t(x)\)는 초기 상태에서 시작해서 정책 \(\pi\)를 따랐을 때 \(t\)시점에 상태 \(\mathbf{x}\)에 도달할 확률이다. 즉,
이때, \(d_0\)는 환경 초기 상태의 확률분포이다. Proto-RL에서는 \(d^{\pi}(\cdot)\)의 엔트로피에 비례하여 intrinsic reward를 정의할 것이다. 확률변수 \(X\)에 대한 엔트로피는 다음과 같이 정의된다.
기댓값으로 표현되는 실제 엔트로피 값을 정확하게 계산하는 것은 어렵기 때문에 보통 데이터를 사용하여 엔트로피를 추정하게 된다. 가장 단순한 추정 방법은 \(p(X)\)에서 데이터 \(N\)개를 샘플링하여 기댓값을 추정하는 것이다. \(N\)개의 데이터를 모아놓은 집합 \(\mathbf{X} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}\)을 하자. \(\mathbf{X}\)로 추정한 엔트로피는 다음과 같다.
하지만 우리의 경우 환경과 상호작용하여 샘플은 얻을 수 있을 언정 밀도함수 \(d^{\pi}(\mathbf{x})\) 값을 계산하는 것이 불가능하다. 따라서, 다른 엔트로피 추정 방식인 non-parametric Nearest Neighbor 기반 엔트로피 추정 방식을 택한다:
이때, \(k\)는 사용자가 설정할 하이퍼파라미터이고 \(q\)는 상태 공간의 차원이다 (\( \mathbf{x} \in \mathbb{R}^q\)). 그리고 \(\Gamma\)는 gamma 함수고 \(C_k=\ln k - \frac{\Gamma'(k)}{\Gamma(k)}\)는 bias correction을 위한 항이며 관심 없는 대상이다. 우리가 관심 있는 것은 \(R_{i, k, \mathbf{X}} = \lVert \mathbf{x}_i - \text{NN}_{k, \mathbf{X}} (x_i)\rVert\)인데, 여기서 \(\text{NN}_{k , \mathbf{X}} (x_i)\)는 데이터셋 \(\mathbf{X}\)에서 \(\mathbf{x}_i\)의 \(k\)번째 최근접 이웃이다. 직관적인 해석은 다음과 같다.
최근접 이웃과 거리가 짧다 \(\rightarrow\) 데이터가 몰려있다 \(\rightarrow\) 엔트로피가 작다. 실제로, 분모가 작아지고, \(\ln\) 값은 커지며 마이너스가 붙어 엔트로피 추정치는 작아진다.
최근접 이웃과 거리가 멀다 \(\rightarrow\) 데이터가 퍼져있다 \(\rightarrow\) 엔트로피가 크다. 실제로 분포가 커지고 \(\ln\) 값은 작아지며 마이너스가 붙어 엔트로피 추정치는 커진다.
사실 엔트로피를 정확하게 추정하여 intrinsic reward를 정의할 필요는 없기 때문에 그냥 엔트로피 추정치에 비례하게 보상함수를 정의하게 된다.
원래 \(d^{\pi}(\mathbf{x})\)의 엔트로피를 고려하려고 했으나 \(\mathbf{x}\)가 고차원이기 때문에 latent vector \(\mathbf{z}\)를 사용한다. 그리고 전체 데이터셋 \(X\)에서 상태 \(\mathbf{x}\)의 \(k\)번 째 최근접 이웃을 찾기는 어렵기 때문에 미리 샘플링 해놓은 latent vector들의 집합인 \(\mathbf{Q}\)에서 \(k\)번 째 최근접 이웃을 찾게 된다.
\(\mathbf{Q}\)는 replay buffer처럼 사이즈가 고정된 큐 자료구조이며, 학습 동안 계속 데이터가 나갔다 들어온다. 미니 배치 \(\left\{ \mathbf{x}_i \right\}_{i=1}^{B}\)가 들어오면 latent vector \(\left\{ \mathbf{z}_i \right\}_{i=1}^{B}\)들이 prototype \(\left\{ \mathbf{c}_j \right\}_{j=1}^{M}\)에 속할 확률을 담은 행렬 \(\mathbf{W}\)을 계산한다.
그럼 각 prototypes \(\mathbf{c}_j\)마다 가중치 \(\left\{ w^{i}_j \mid i=1,\ldots B \right\}\)를 사용하여 latent vector 1개씩 뽑아 총 \(M\)개의 latent vectors를 \(\mathbf{Q}\)에 집어 넣는다. 이 과정 통해 \(\mathbf{Q}\)에는 가장 최근 \(T=4\)개 미니 배치에 대해 각 \(M\)개의 latent vectors가 저장되어 총 \(MT=512 \times 4 = 2048\)개의 latent vectors가 저장되게 된다.
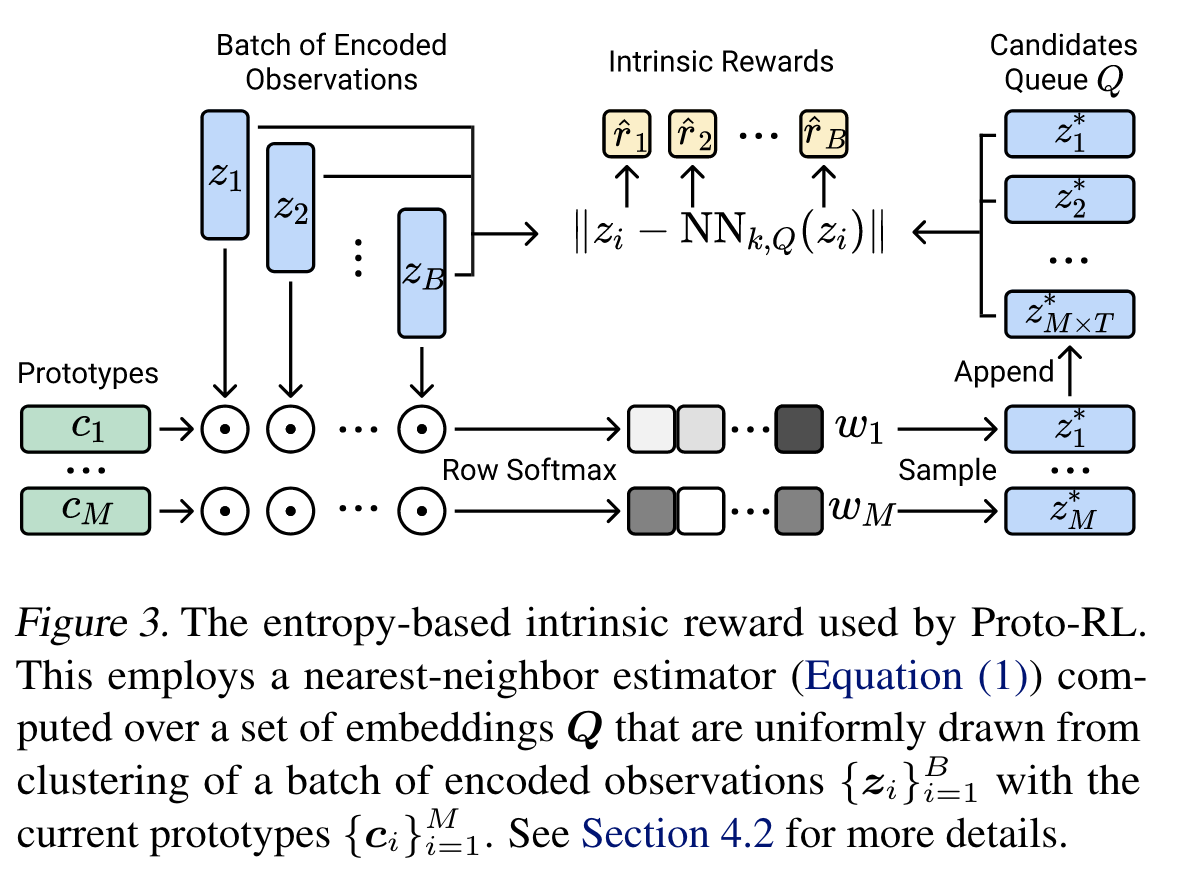
미니 배치 내 각 데이터 \(\mathbf{x}_i\)마다 \(\mathbf{Q}\) 에 저장된 \(2048\)개의 latent vectors로부터 \(k\)번 째 최근접 이웃을 계산하고, intrinsic reward \(\hat{r}_i\)를 계산한다. 이 intrinsic reward를 사용하여 SAC 알고리즘을 적용하면 끝이다. 참고로 Unsupervised RL 단계에서는 intrinsic reward 사용하고, 미세조정 단계에서는 task reward와 intrisic reward를 가중합한 것을 보상으로 정의하여 사용한다 (\(r_t + \alpha \hat{r}_{t}\)):
