High variance across runs / failed runs#

  • 제목: Is High Variance Unavoidable in RL? A Case Study in Continuous Control

  • 저자: Bjorck, Johan, Carla P. Gomes, and Kilian Q. Weinberger, Cornell University

  • 연도: 2022년

  • 학술대회: ICLR

  • 링크: http://arxiv.org/abs/2110.11222

  • 키워드: Off-policy, failed runs, stabilize learning


강화학습 알고리즘은 코드에 전혀 문제가 없더라도 랜덤 시드에 따라서 학습이 잘 될 때도 있고 반대로 학습이 아예 안 되어서 학습 곡선이 바닥을 길 때도 있다. 이 논문은 강화학습 알고리즘이 실행들 사이의 (across runs) 큰 분산을 갖는 현상을 분석하고 해결한 논문이다. 특히, runs 사이의 큰 분산의 주된 원인으로 학습이 아예 실패한 failed runs을 지목하고 이 failed runs를 줄이는 방법에 대해 소개한다. 실험을 진행한 세팅이 조금 제한적이긴 하지만 강화학습 연구자/실무자들이 종종 경험하는 이유도 모른 채로 학습에 실패하는 현상을 다룬다는 점에서 매우 흥미로운 논문인 것 같다. 포스팅에서 언급하는 모든 분산에 관한 이야기는 runs 사이의 분산을 말한다.


논문에서 사용한 알고리즘 및 환경#

이 논문에서는 특히 runs 사이의 variance가 크다고 알려진 “continuous control from pixels with an actor-critic agent” 세팅에 집중하고 있다. 따라서 환경은 DeepMind Control suite (DMC) 중 medium과 hard로 분류된 총 21개의 환경에 대해서 실험이 진행됐다. 기존 state 대신 image observation을 사용했다. 주된 분석 대상이 될 베이스라인 알고리즘은 DrQ-v2 [YFLP21] 이며 필자가 읽진 않았지만 논문상에서는 DDPG 알고리즘에 data augmentation 기법이 적용된 알고리즘이라고 한다. 즉, 이 논문은 off-policy 알고리즘의 failed runs를 분석한 논문이다.


Empirical evidence#

DrQ-v2 알고리즘이 runs 사이의 큰 분산을 갖는다는 경험적 증거는 다음과 같다. DMC의 21개 tasks 중 DrQ-v2 알고리즘이 유독 큰 분산을 보이는 5개의 tasks (finger turn hard, walker walk, hopper hop, acrobot swingup, and reacher hard)에 대해서 시드를 바꿔가며 40개의 에이전트를 1,000,000 environment steps (=1,000 에피소드) 동안 학습시켰다.


아래의 그림의 첫 번째 행은 40개 학습 곡선의 평균 (파란색 선)과 1표준편차 (음영)을 보여주고, 두 번째 행은 각 runs의 개별 학습 곡선이다. walker walk와 hopper hop의 경우 1,000 에피소드 내내 학습이 전혀 되지 않아 학습 곡선이 바닥에 붙어 있는 runs들이 많이 보인다. 이러한 학습에 실패한 runs를 논문에서는 outlier runs라고 부르지만 필자는 그냥 failed runs라고 부를 것이다.

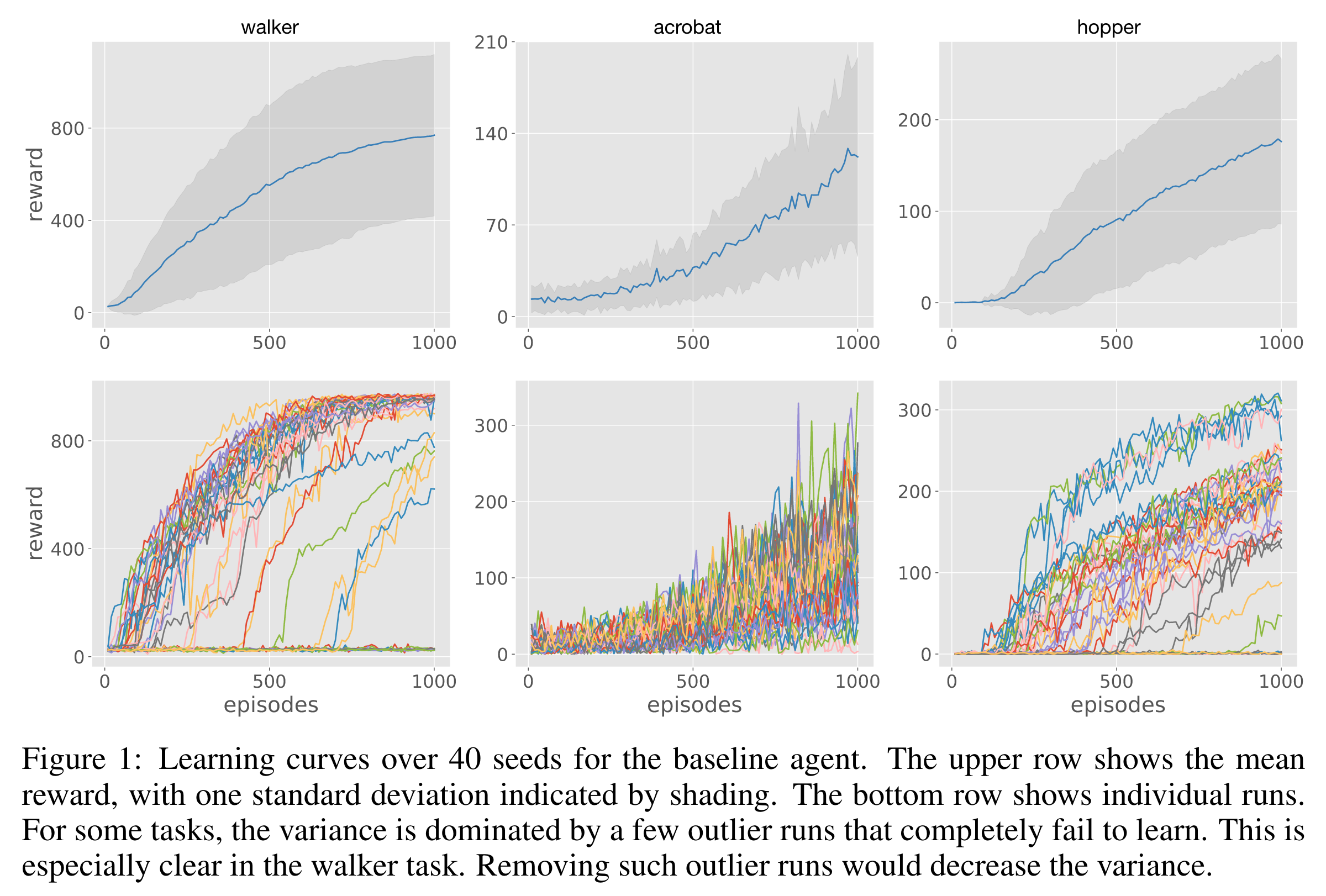
../../_images/240109_figure1.png

위와 같은 현상은 환경과 알고리즘이 다를지라도 나를 포함한 많은 사람들이 경험해보았을 것이다. 그리고 보통 사람들 같으면 이 현상을 마주했을 때 랜덤 시드를 탓하며 다른 시드로 다시 코드를 돌렸을 것이다. 하지만 논문의 저자는 failed runs가 발생한 이유를 집요하게 밝혀내려고 다양한 실험을 했다. 우선 직관적으로 생각해볼 수 있는 원인들은 다음과 같을 것이다.

  • 네트워크 파라미터의 초기화에 의존하여 runs의 성패가 달릴 것이다.

  • 환경의 무작위성에 의해 운 나쁘게도 나쁜 상태만 방문했을 것이다.

  • 학습 초기에 만들어 내는 observations에 대한 representation이 안 좋아서 안 좋은 방향으로 학습됐을 것이다.


나도 동일하게 생각했다. 네트워크 파라미터가 안 좋게 초기화되는 등 여러 무작위성에 의해 학습 초기에 네트워크들이 안 좋은 곳으로 수렴해서 발생한 문제라고 생각했다. 하지만 논문에서는 위 세 가지는 failed runs를 만드는 직접적인 이유가 아니라고 실험을 통해 주장한다.


Does initialization matter?#

초기 네트워크 파라미터와 랜덤 행동으로 모은 initial buffer를 완전히 일치시킨 후 학습을 시작한 2개의 runs A와 B에 대해서 학습 곡선의 correlation을 계산하였다. 두 runs의 학습 곡선이 비슷하면 correlation이 높을 것이고, 학습 곡선이 다르면 correlation이 0에 가까울 것이다. 이 실험을 10개의 initialization 세팅에 대해서 진행하여 10개의 correlation을 얻어 평균을 내렸다.


아래 그림의 왼쪽 그림을 보면 동일한 initialization으로 시작한 두 runs의 correlation이 모두 작은 것을 확인할 수 있다. 즉, initialization이 같아도 어쩔 땐 학습에 성공하고 어쩔 땐 학습에 실패한다는 말이니, network initialization 및 initial buffer가 큰 분산을 만들어내는 요소가 아니라는 것을 알 수 있다.

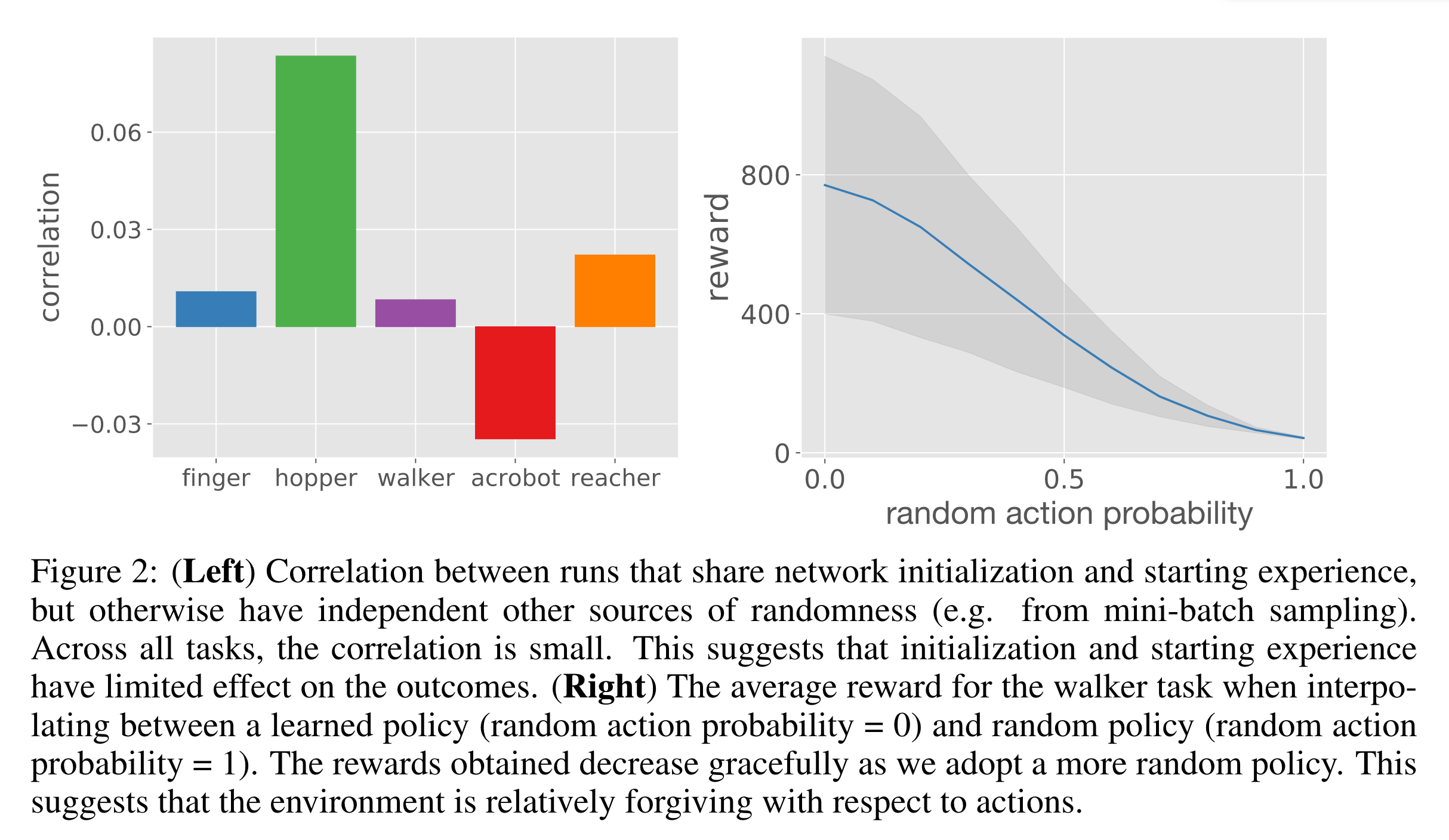
../../_images/240109_figure2.png

Are the environments too sensitive?#

환경의 무작위성 때문에 runs들 사이의 성능의 분산이 큰 것일까? 만약 정말 정밀한 정책만이 환경을 제어하여 좋은 보상을 받을 수 있다면, 에이전트가 우연히 좋은 상태와 행동을 방문하지 못할 경우 학습에 실패할 것이다. 에어전트가 성능 향상 시작의 트리거가 되는 상태와 행동을 방문하지 못했기 때문일까? 환경을 제어하기 위해 정말 특정한 정책이 필요한 경우, 다른 말로 환경에서 받을 수 있는 누적 보상의 크기가 정책 변화 민감한 경우 때문에 분산이 커지는 것일까? 이를 확인하기 위해서 환경 제어에 성공한 정책을 하나 선택했다. 그리고 이 정책으로 환경을 제어할 때 매 스탭마다 \(p\)의 확률로 랜덤 행동을 취하게 만들어서 누적 보상이 어떻게 달라지는 확인했다.


\(p\)값에 따른 누적 보상의 변화 그림은 위 그림의 오른쪽 그림과 같다. 랜덤 행동을 취하는 꽤나 파멸적인 정책인데도 누적 보상이 잘 방어되는 것을 알 수 있다. 따라서 환경이 정책 변화에 완전히 민감하지 않다는 것을 알 수 있다. 환경에 의해 발생하는 분산 때문에 runs들 사이의 분산이 커졌다고 보기 어렵다는 것이다. (사실 이 실험을 통해 말하고자 하는 것이 무엇인지 잘 모르겠다.)


Is feature learning to blame?#

Actor와 critic에 사용되는 image encoder는 학습 초기에는 학습이 덜 돼서 observation에 대한 좋은 representation을 만들지 못할 것이다. 따라서 학습 초기에는 actor가 관심 있는 행동을 만들지 못할 것이고 이로 인해 다시 좋지 않은 representation을 만드는 악순환이 반복될 것이다. 그렇다면 과연 학습 초기 image encoder가 observation에 대한 잘못된 representation을 생성하는 것이 failed runs의 원인일까?


이를 확인하기 위하여 학습 종료 후 평균 이상의 성능을 보인 에이전트를 선택하고 학습 중간 지점(500 episodes)의 네트워크 파라미터를 초기 네트워크 파라미터로 설정하여 새롭게 에이전트를 학습시키는 실험을 진행했다 (pretrain, pretrain + low lr). 그리고 사전 훈련된 네트워크를 사용하지 않고 학습 초기 첫 10K/20K 스탭에 self-supervised learning (ssl) 손실 함수를 추가하여 image encoder가 좋은 representation을 만들어낼 수 있도록 만든 에이전트들 (self-supervised 10K/20k)도 비교했다.


실험 결과는 아래 표와 같다. 가장 오른쪽 컬럼을 보면 사전 훈련된 네트워크를 사용하는 것과 ssl을 사용하는 것이 runs들 사이의 분산을 크게 줄여주지 못하는 것을 알 수 있다. 즉, 좋은 image encoder를 사용하여 좋은 representation을 만들어도 학습에 실패할 runs들은 실패한다는 것이다.

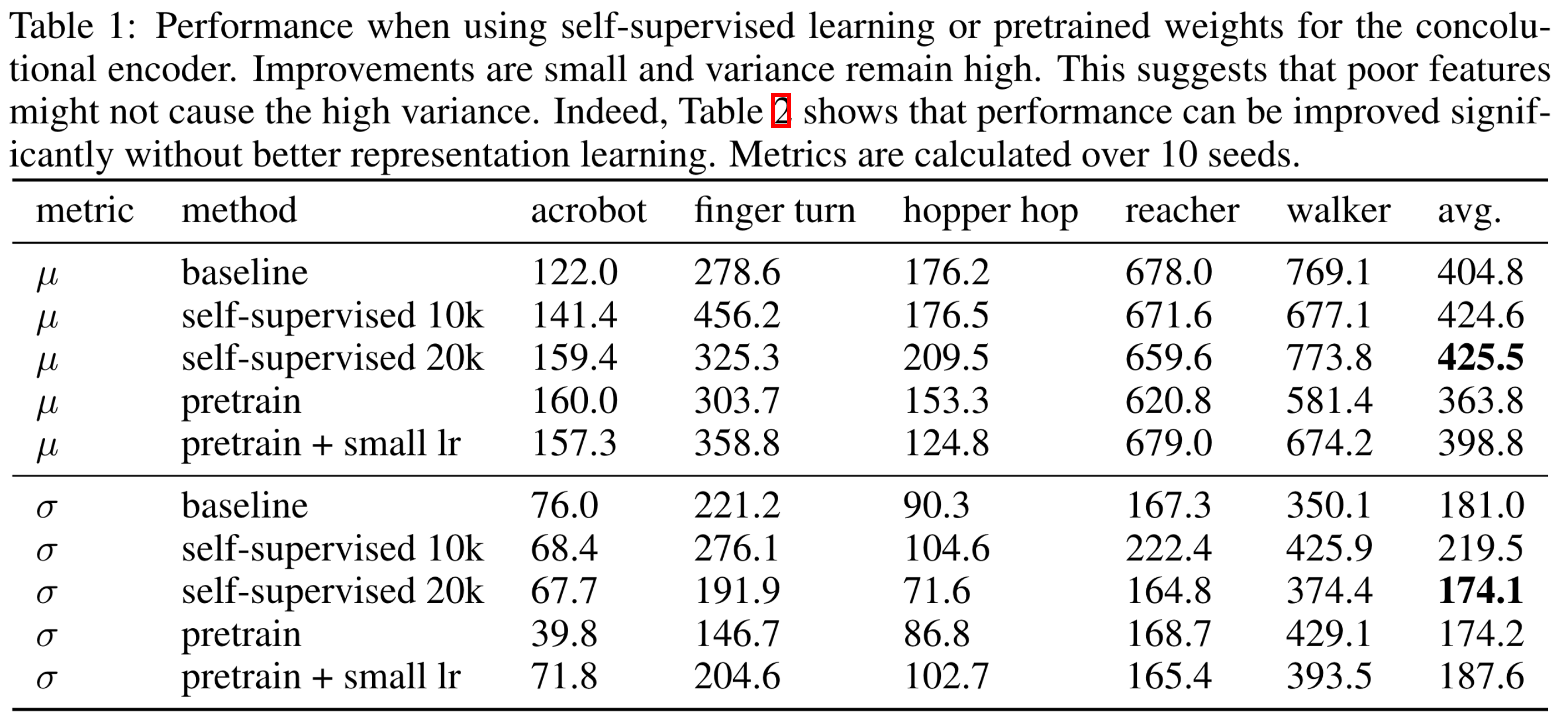
../../_images/240109_table1.png

논문에서 제시하는 큰 분산의 원인#

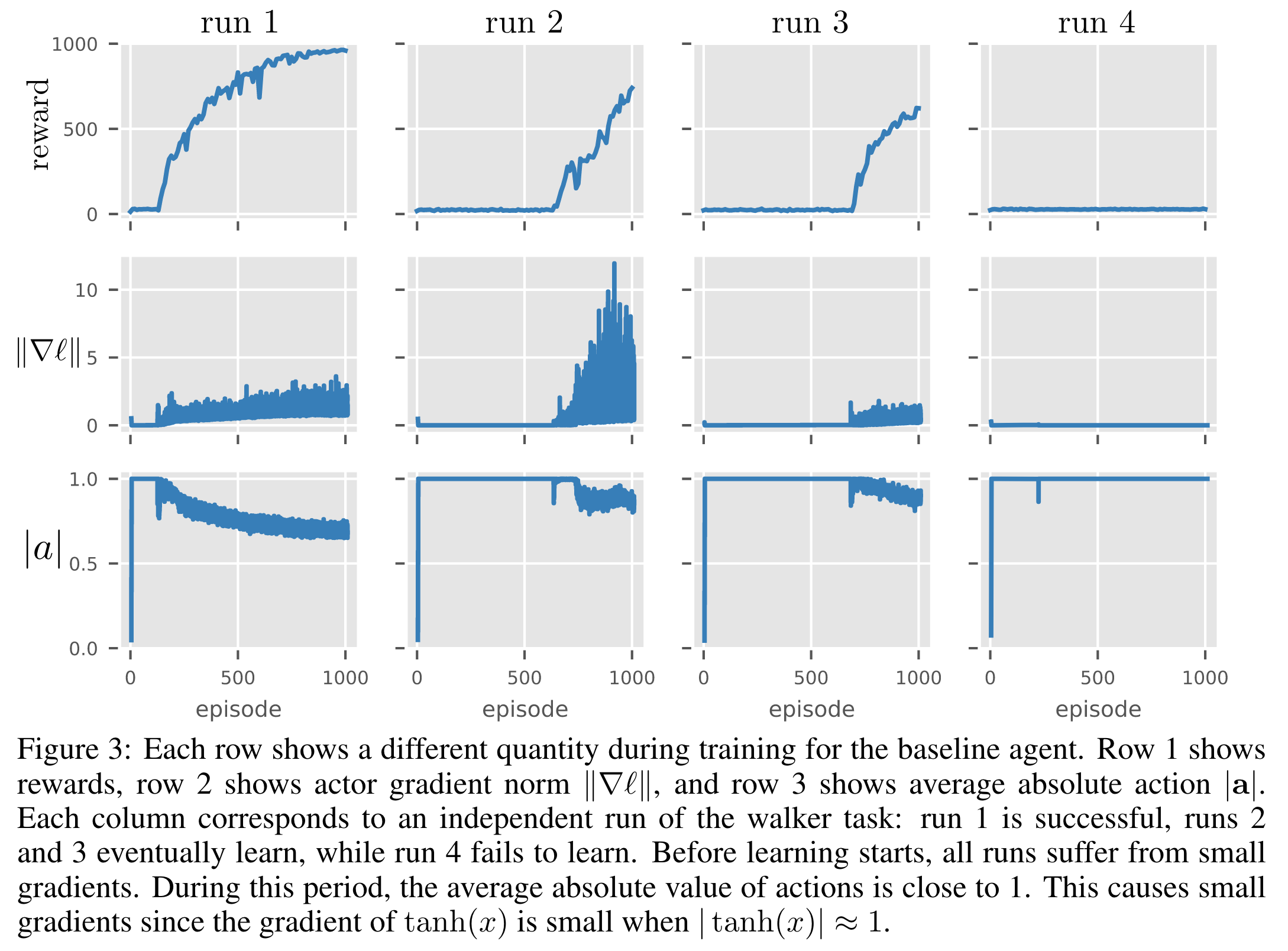
논문에서 failed runs에는 어떤 문제가 있는지 확인하기 위하여 여러 형태의 학습 곡선을 갖는 run들에 대하여 스탭별 정책 네트워크의 그레디언트 norm과 행동의 절댓값을 살펴보았다. 아래는 walker walk 환경에서 네 개의 runs에 대한 결과이다. \(|\mathbf{a}|\)는 행동 \(\mathbf{a}\)의 각 원소의 절댓값의 평균을 나타내는 표기이다. 2~4번 열을 비교해보면 행동의 절댓값이 \(\pm 1\) 근처에 있는 동안에는 actor의 그레디언트의 norm이 0에 가깝다. 그레디언트가 0이기 때문에 학습이 일어나지 않는 것이다. Continuous 환경에서는 주로 actor network의 마지막 출력 전 (\(\mathbf{a}^{\text{pre}}_\theta\) 로 표기)에 hyperbolic tangent (tanh)를 적용하여 -1과 1 사이의 값으로 바꿔준다. tanh 함수의 경우 \(\pm 1\)에서 그레디언트가 0이다. tanh 함수의 값이 \(\pm 1\)에 가깝다는 것은 \(\mathbf{a}^{\text{pre}}_\theta\)의 각 원소가 아주 큰 양수값 또는 아주 작은 음수값이라는 것을 의미한다.

../../_images/240109_figure3.png

논문에서 제시한 간단한 해결책#

위에서 \(\mathbf{a}^{\text{pre}_\theta}\)의 원소들의 절댓값이 아주 클 때 학습이 일어나지 않는 것을 확인했다. 이 논문에서 penultimate normalization을 제안한다. 처음에 penultimate라는 단어가 패널티와 연관이 되어 있어서 패널티를 주는 방법론인줄 알았다. 하지만 penultimate는 ‘끝에서 두 번째의’라는 뜻이다. penultimate normalization는 \(\mathbf{a}^{\text{pre}}_\theta\) 직전의 activation을 \(\Lambda_\theta(\mathbf{s})\)라고 할 때, 먼저 \(\Lambda_\theta(\mathbf{s})\)를 normalization해줘 유닛 벡터를 계산한다.

\[\Lambda_\theta^{\text{n}}(\mathbf{s}):=\Lambda_\theta(\mathbf{s}) / \lVert \Lambda_\theta(\mathbf{s}) \rVert.\]

위 식이 penultimate normalization, 줄여서 pnorm이다. 여기서 actor network의 경우 \(\Lambda_\theta^{\text{n}}(\mathbf{s})\)의 차원을 행동공간의 차원으로 바꿔주기 위하여 행렬 \(L\)을 곱해준 것을 \(\mathbf{a}_\theta^{\text{pre}}\)로 사용한다.

\[\mathbf{a}_\theta^{\text{pre}}:=L\Lambda_\theta^{\text{n}}(\mathbf{s}).\]

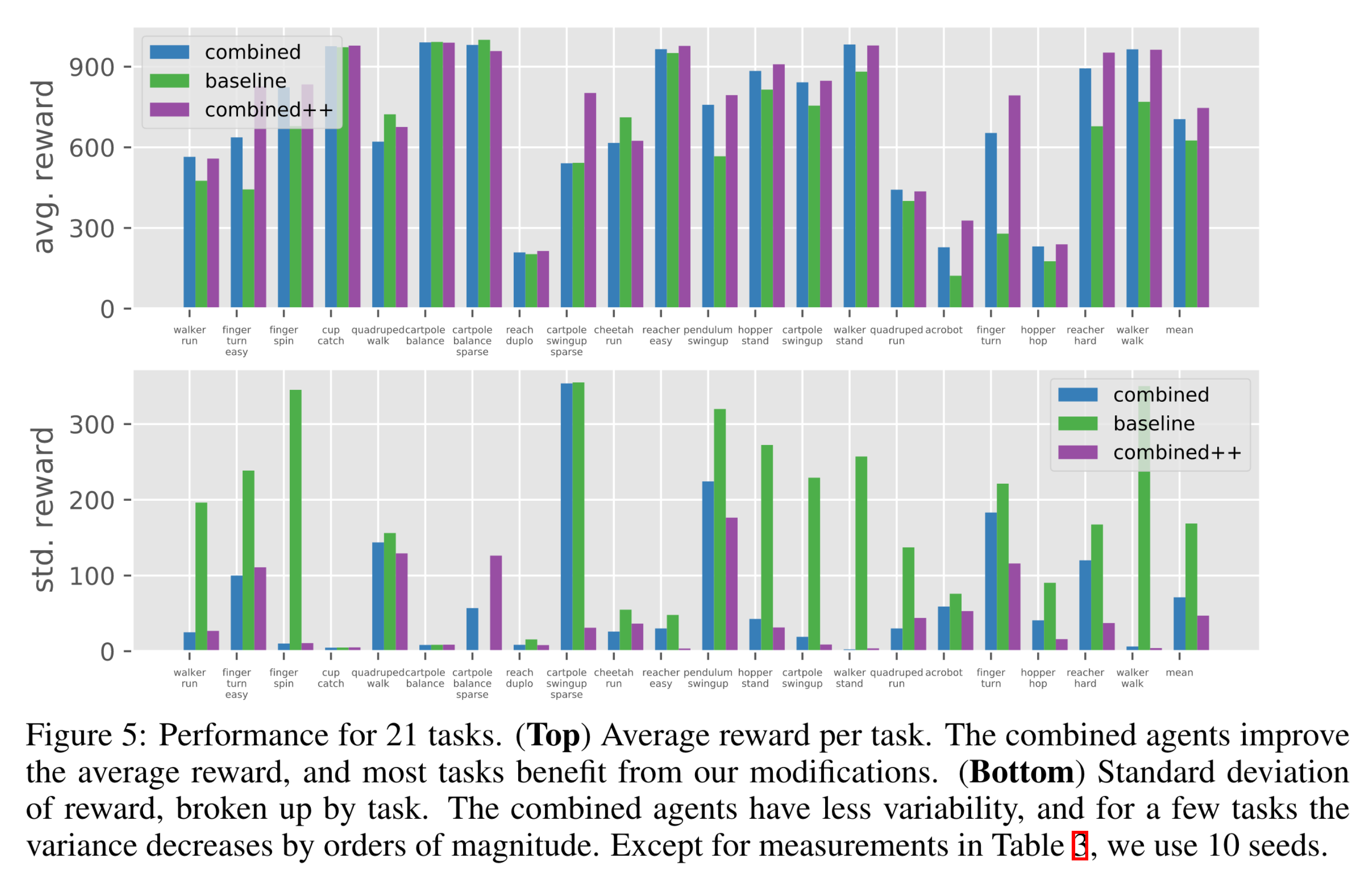
이 pnorm을 actor와 critic 네트워크 둘 다에 적용하고, ssl을 학습 과정 전체 동안 진행하며, 손실 함수에 \(\mathbf{a}^{\text{pre}}_\theta\)의 크기에 패널티를 준 알고리즘 (combined)을 사용하여 베이스라인인 DrQ-v2와 비교한 그림은 다음과 같다. 위 그림은 환경별 10개 runs에 대한 평균 누적 보상이고, 아래 그림은 표준편차이다. combined++은 combined에 sparse reward 환경을 위해 2가지 구현 디테일을 추가해준 것이다.

../../_images/240109_figure5.png

마치며#

우리가 흔히 경험하는 학습에 실패하는 현상의 원인을 파악하고 해결했다는 점에서 굉장히 좋은 논문인 것 같다. 나는 학습에 실패하면 자연스러운 현상으로 간주하고 내 코드를 의심하거나 랜덤 시드와 하이퍼파라미터 등만 바꿔가며 다시 돌렸을텐데, 저자는 원인을 어떻게든 파악하려고 했다는 점을 본받고 싶다. 문제의 원인을 파악하면 해결책도 따라오는 것 같다. 그렇게 하나의 논문이 탄생하는 것 같다.

생각해볼 점은 내 짧은 경험으로는 on-policy 알고리즘들이 runs 사이의 분산이 더 큰 것으로 알고 있다. On-policy 알고리즘들이 하이퍼파라미터와 코드 디테일에도 더욱 민감한 것 같다. On-policy에 대해서도 이 논문의 분석과 해결책이 성립할지 궁금하다.


참고 문헌#

YFLP21

Denis Yarats, Rob Fergus, Alessandro Lazaric, and Lerrel Pinto. Mastering visual continuous control: improved data-augmented reinforcement learning. 2021. arXiv:2107.09645.