Learning Invariant predictor with Selective Augmentation (LISA)
Contents
Learning Invariant predictor with Selective Augmentation (LISA)#
제목: Improving Out-of-Distribution Robustness via Selective Augmentation
저자: Cabrera-Vives, Guillermo, César Bolivar, Francisco Förster, Alejandra M. Muñoz Arancibia, Manuel Pérez-Carrasco, and Esteban Reyes
연도: 2023년
학술대회: ICML
키워드: Invariant to domain shift
Overview#
공개된 데이터셋으로 학습한 모델을 내가 갖고 있는 데이터에 대해 예측을 해보면 잘 안 될 때가 많다. 예를 들어, A병원, B병원, C병원에서 공개한 많은 양의 데이터로 모델을 학습시키고 이를 D병원 데이터에 예측을 해보면 성능이 좋지 않을 것이다. A~C병원이 갖는 데이터의 분포와 D병원 데이터의 분포가 서로 다르기 때문일 것이다. 이 논문은 훈련 데이터의 분포와 테스트 데이터의 분포가 서로 달라도, 즉 domain shift가 있어도 잘 작동하는 모델을 학습시키는 방법에 관한 것이다. 특히, data augmentation 기법을 적용하여 domain shift에 robust한 모델을 학습시킨다. 이 논문의 요약은 다음 2줄로 충분하다.
Inter label LISA: 레이블은 같지만 도메인이 서로 다른 두 데이터를 interpolation.
Inter domain LISA: 도메인은 같지만 레이블이 서로 다른 두 데이터를 interpolation. 이때 레이블도 같은 비율로 interpolation
Methodology#
훈련 데이터의 \(i\) 번째 데이터를 \((x_i, y_i, d_i)\)라고 하자. \(x_i\)는 입력 데이터이며 컴퓨터 비전의 경우 이미지이고, 텍스트 데이터의 경우 pretrained LLM이 출력한 임베딩 벡터가 된다. \(y_i\)는 레이블이며 이 논문의 경우 classification을 다루기 때문에 \(y_i\)는 원핫인코딩 벡터가 된다. \(d_i\)는 \(i\)번째 데이터가 속한 도메인이다. 이 논문에서는 각 데이터가 속한 도메인을 알고 있다고 가정한다. 각 데이터가 속한 도메인을 모르는 경우는 훨씬 더 어렵지만 흥미로운 연구 주제가 될 것이다.
각 훈련 데이터 \((x_i, y_i, d_i)\)마다 가장 먼저 \(\text{Beta}(2, 2)\)에서 interpolation ratio \(\lambda\)를 샘플링한다. 다음으로 \(p_{\text{sel}}\)의 확률로 inter-label LISA를 적용할지, inter-domain LISA를 적용할지 결정한다. \(p_{\text{sel}} \in [0,1]\)은 하이퍼파라미터이며, inter label LISA를 적용할 확률이다. 논문에서는 cross-validation을 통해 좋은 \(p_{\text{sel}}\)을 찾았으며, \(p_{\text{sel}}=0.5\) 혹은 \(p_{\text{sel}}=1\)이 잘 작동한다고 한다.
만약 inter-label LISA가 선택되었다면, 훈련 데이터에서 레이블은 \(y_i\)와 같으며 도메인은 \(d_i\)와 다른 데이터 \((x_j, y_j, d_j)\)를 랜덤 샘플링한다.
만약 inter-label LISA가 선택되었다면, 훈련 데이터에서 레이블은 \(y_i\)와 다르며 도메인은 \(d_i\)와 같은 데이터 \((x_j, y_j, d_j)\)를 랜덤 샘플링한다.
그리고 다음과 같이 interpolation한 \(x_{\text{mix}}\)와 \(y_{\text{mix}}\)를 계산한다.
여기서 inter-label LISA의 경우 \(y_{\text{mix}}\)는 \(y_i\)랑 같다. inter-domain LISA의 레이블 \(y_{\text{mix}}\) 경우, 예를 들어, \(y_i=[1, 0]\), \(y_j=[0, 1]\)이고 \(\lambda=0.3\)이라고 했을 때, \(y_{\text{mix}}= [0.3, 0.7]\)이 된다. 이렇게 만든 \(x_{\text{mix}}\)와 \(y_{\text{mix}}\)로 모델을 학습시키는 것이다. 논문에서 사용된 LISA 설명 그림은 다음과 같다.
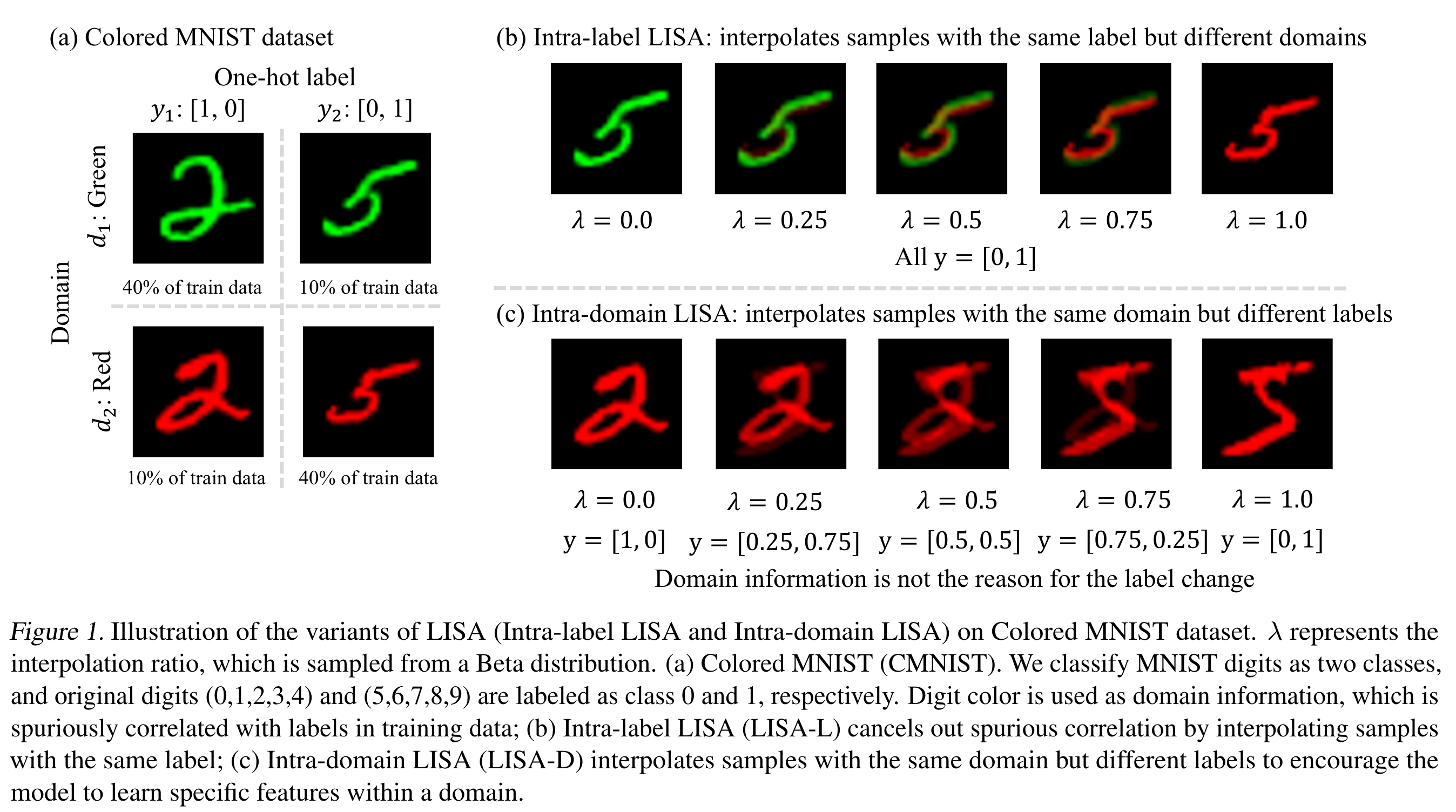
예시에 샤용된 데이터셋은 CMNIST이며 0~4의 숫자는 0으로, 5~9의 숫자는 1로 레이블링되어 있다. 데이터의 도메인은 초록색 글자와 빨간색 글자로 2가지가 있다. 이 데이터셋의 경우 초록색 글자 데이터의 80%가 레이블 0에 속하며 20%는 레이블 1에 속한다. 반대로 빨간색 글자의 80%는 레이블 1에 속하며 20%는 레이블 0에 속한다. 즉, 숫자의 모양에 상관 없이 글자가 초록색이면 0이라고 예측하고 빨간색이면 1이라고 예측하면 높은 성능이 보장된다. 이런 잘못된 상관 관계를 논문에서는 spurious correlation (허위 상관)이라고 부르고 있다. 테스트 데이터도 초록색 글자와 빨간색 글자가 있으며, 다만 색상별 레이블의 비율은 8:2가 아니라 9:1이다. 이렇게 테스트 데이터의 도메인이 훈련 데이터의 도메인과 일치하지만 그 분포가 다른 문제를 subpopulation
그림의 첫 번째 행이 inter-label LISA 기법이다. 레이블은 \(y_2\)로 같으며 도메인이 다른 빨간색 글자 이미지와 interpolation되어 초록색과 빨간색 모두를 포함하는 글자의 이미지가 되었다. 두 번째 행은 inter-domain LISA 기법으로, 도메인은 빨간색 글자로 같으며 레이블이 서로 다른 두 글자를 합치고 레이블도 대응하게 interpolation하였다. 사실 이런 데이터 기법을 mixup이라고 부른다. 다만 mixup은 전체 데이터에서 임의로 두 샘플을 뽑아 interpolation하는 방법이다. 하지만 mixup만으로는 domain shift에 robust한 모델을 만들기 부족하여 선택적으로 샘플을 선택하는 selective augmentation 적용한 것이 LISA이다.
Results#
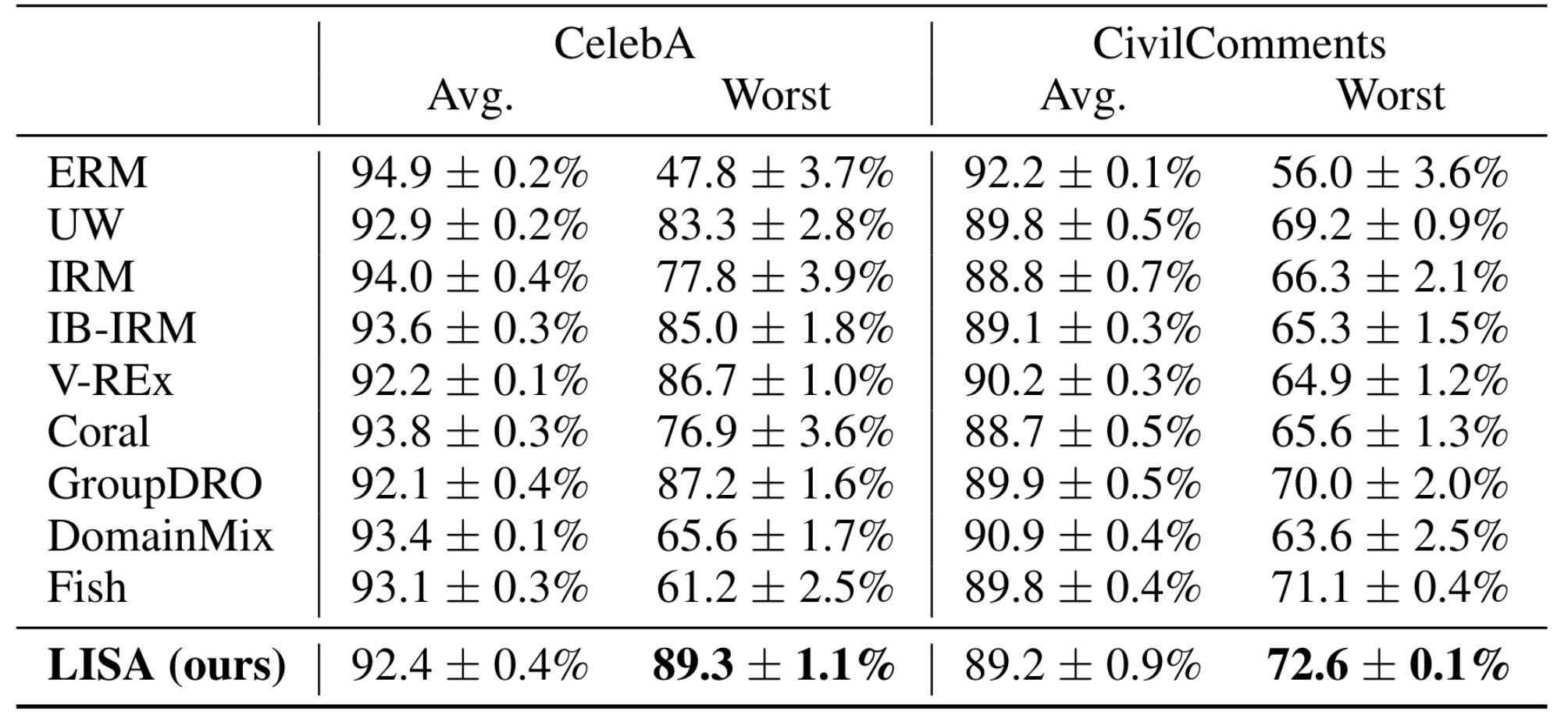
아래는 subpolulation shift를 갖고 있는 데이터셋에 대한 성능표이다. 논문의 본문이 아닌 부록에 있는 표이다. CelebA는 이미지 데이터셋이며 CivilComments는 텍스트 데이터셋이다. Avg가 도메인 상관 없이 측정 없이 정확도를 측정한 지표이고, worst가 도메인별로 나눠서 정확도를 측정했을 때, 가장 성능이 낮은 도메인에 대한 정확도이다. 그리고 ERM이 우리가 아는 평범한 손실 함수를 사용한 모델이다. ERM의 결과를 해석해보자면, 우리가 검증 데이터로 90%대의 정확도를 얻었는데, 실제로 테스트 해보니 어떤 도메인에서는 성능이 50%까지 떨어진다는 것을 의미한다. LISA는 가장 안 좋은 도메인에 대한 성능을 거의 90%까지 끌어올렸다.
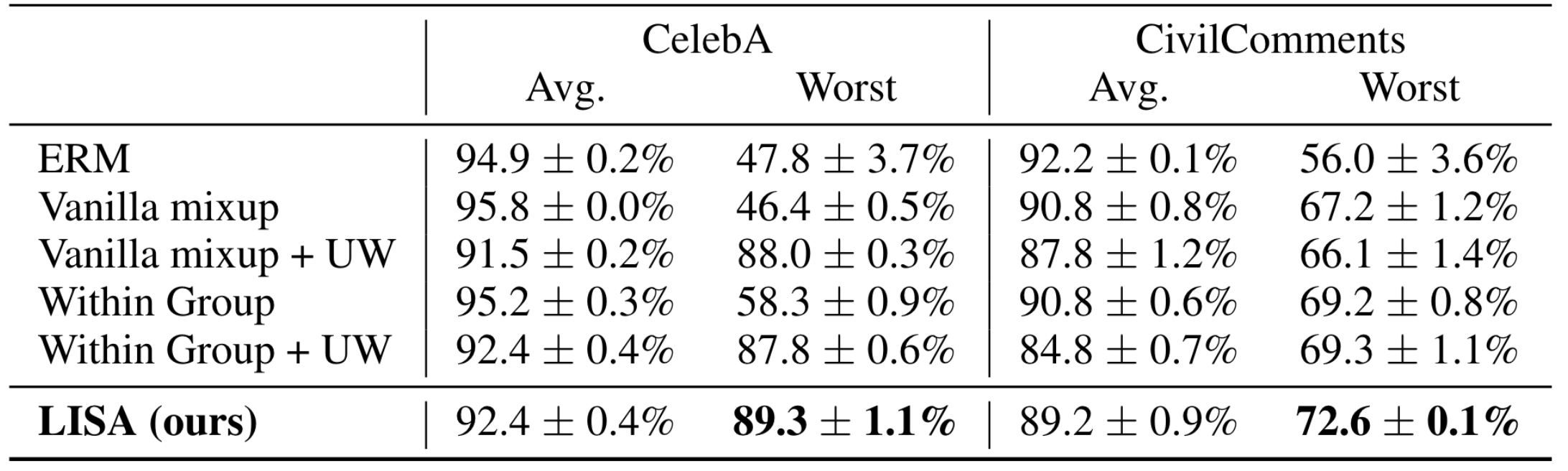
아래는 위 데이터셋에 대한 ablation study 결과이다. 마찬가지로 부록에 있는 표를 갖고 왔다. Vanilla mixup은 selective augmentation 없이 mixup을 진행한 것이고, Within group 같은 그룹 다른 레이블에 대한 데이터만 interpolation을 한 결과이다. UW는 upweighting을 의미하며 논문에 설명은 없지만 minor class에 대한 oversampling을 의미하는 것 같다. 먼저, 논문에서 주장한 것처럼 mixup만으로는 subpopulation shift 문제가 해결되지 않는다. 그래서 LISA의 성능 향상이 단순히 data augmentation에 기인하는 것이 아닌 것을 알 수 있다.
위 결과말고도 논문에 domain shift에 대한 결과도 많이 있으니 필요하신 분들께서는 추가적으로 논문을 살펴보면 좋을 것 같다.
