Conservative Q-Learning (CQL)#

1. 풀고자 하는 문제#

1.1 Offline RL과 distribution shift#

환경과 상호작용하며 에이전트를 학습시키는 기존 강화학습과 다르게, offline RL은 환경과 상호작용할 수 없으며, 미리 수집된 transitions 데이터셋을 사용하여 에이전트를 학습시킨다. 미리 수집된 데이터셋 \(\mathcal{D}\)는 어떤 행동 정책 \(\pi_\beta\)에 의해 만들어졌다고 가정하며, 최소 그 행동 정책과 비슷한 수준의 정책 또는 더 좋은 정책 \(\pi\)를 찾는 것을 목표로 한다.

이때,

  • 데이터셋에 있는 state-action pair \((\mathbf{s},\mathbf{a})\in\mathcal{D}\)의 empirical 분포와

  • 학습된 정책 \(\pi\)가 만드는 state-action pair \((\mathbf{s}, \mathbf{a})\) where \(\mathbf{s} \in \mathcal{D}\) and \(\mathbf{a} \sim \pi(\cdot|\mathbf{s})\)의 분포가

다를 수 있으며, 이를 distributional shift라고 부른다. Online RL의 경우 학습된 정책으로 직접 환경과 상호작용하여 이전에 보지 못한 state-action pair을 경험해볼 수 있지만, offline RL의 경우 환경과 상호작용할 수 없기 때문에 학습된 정책으로 만든 state-action pair에 에러가 있을 경우 이를 correction할 수 없다.


1.2 Distribution shift의 문제점 알아보기#

Distribution shift가 Q-learning에 미치는 영향을 알아보기 위해 먼저 Bellman operator를 떠올려보자.

\[ \begin{equation} \mathcal{B}^\pi Q^{\pi}(\mathbf{s, \mathbf{a}}) = r(\mathbf{s, \mathbf{a}}) + \gamma \mathbb{E}_{s' \sim p(\cdot|\mathbf{s}, \mathbf{a}), a' \in \pi(\cdot|\mathbf{s'})}\left[ Q^\pi(\mathbf{s'}, \mathbf{a'})\right]. \end{equation} \]

일반적으로 reward function \(r\)과 transition probability distribution \(p\)를 알 수 없기 때문에, buffer \(\mathcal{D}\)에 있는 transition \((\mathbf{s}, \mathbf{a}, r, \mathbf{s}')\)을 사용하여 행동가치함수를 학습한다. Empirical Bellman operator \(\hat{\mathcal{B}}\)는 다음과 같다.

\[ \hat{\mathcal{B}}^\pi Q^{\pi}(\mathbf{s, \mathbf{a}}) = r + \gamma \mathbb{E}_{\mathbf{a}' \sim \hat{\pi}(\cdot | \mathbf{s}')}\left[ Q(\mathbf{s}', \mathbf{a}')\right] \; \text{ for } (\mathbf{s}, \mathbf{a}, r, \mathbf{s}') \in \mathcal{D}. \]

보상 \(r\)과 다음 상태 \(\mathbf{s}'\)이 환경 모델로부터 샘플링되는 것이 아니라 그냥 데이터를 대입하는 것이다. Empirical Bellman operator를 바탕으로 TD 에러를 최소화하여 policy evaluation을 하는 것을 식으로 적어보면 다음과 같다.

\[ \hat{Q}^{k+1} \leftarrow \operatorname*{argmin}_{Q}\mathbb{E}_{(\mathbf{s}, \mathbf{a}, r, \mathbf{s}') \in \mathcal{D}} \left[ \left( \left( r +\gamma\mathbb{E}_{\mathbf{a}' \sim \hat{\pi}^k(\cdot | \mathbf{s}')}\left[ \hat{Q}^k(\mathbf{s}', \mathbf{a}')\right]\right) - Q(\mathbf{s}, \mathbf{a}) \right)^2\right]. \]

위 식에서 \((\mathbf{s}, \mathbf{a}, r, \mathbf{s}')\)은 우리가 갖고 있는 데이터이다.

  • 문제가 되는 부분은 정책에서 샘플링한 다음 행동 \(\mathbf{a}'\)에 대해 계산되어야 하는 \(\hat{Q}^k(\mathbf{s}', \mathbf{a}')\)이다.

  • 더 문제가 되는 경우는 우리의 데이터셋 \(\mathcal{D}\)에 \((\mathbf{s}', \mathbf{a}')\)에 대한 transition이 전혀 없는 경우이다. 이런 행동을 out-of-distribution action이라고 부른다.

  • 이보다 더 문제가 되는 경우는 \(\hat{Q}^k(\mathbf{s}', \mathbf{a}')\)이 overestimation 되어 있는 경우이다. Offline RL의 경우 ood action에 대한 행동가치함수 \(\hat{Q}^k(\mathbf{s}', \mathbf{a}')\)는 타겟으로만 사용되고 직접 업데이트되지 않기 때문에 overestimation이 correction 될 수 없다.


이 논문에서는 Conservative Q-Learning (CQL)이라는 알고리즘을 제시하여 overestimation을 근절시킨다. Conservative Q-learning으로 학습한 행동가치함수는 실제 행동가치함수의 lower bound가 된다.


2. Conservative Q-Learning#

2.1 Conservative Off-Policy Evaluation#

Function approximation을 사용하여 행동가치함수를 학습 중일 때, 그냥 단순하게 \(Q(\mathbf{s}, \mathbf{a})\) 값이 낮아지는 방향으로 업데이트를 하면 overestimation이 완화될 것이다. 따라서 다음과 같이 Q-network 업데이트 식에 \(Q(\mathbf{s}, \mathbf{a})\) 최소화하는 텀을 추가할 수 있을 것이다.

\[ \hat{Q}^{k+1} \leftarrow \operatorname*{argmin}_{Q} \left(\textcolor{blue}{ \alpha \mathbb{E}_{\mathbf{s}\sim\mathcal{D}, \mathbf{a}\sim\mu(\cdot|\mathbf{s})}\left[ Q(\mathbf{s}, \mathbf{a}) \right]} + \frac{1}{2} \mathbb{E}_{\mathbf{s}, \mathbf{a} \sim \mathcal{D}} \left[ \left( Q(\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^{\pi}\hat{Q}^k(\mathbf{s}, \mathbf{a}) \right)^2\right] \right). \]

기존의 TD 에러텀에 파란색으로 표시된 부분이 추가된 것 뿐이다. 여기서 \(\mu(\cdot | \mathbf{s})\)는 어떤 특정 분포이다. 만약 OOD 행동에 대해서만 Q값을 최소화하고 싶다면, 상태 \(\mathbf{s}\)에서 ood 행동에만 확률을 부여하는 확률분포 \(\mu(\cdot | \mathbf{s})\)를 구해서 사용하면 된다. 물론 그런 확률분포는 알기 어려울 것이다. 이후에 또 말하겠지만, \(\mu(\mathbf{a}|\mathbf{s}) \propto \exp(Q(\mathbf{s}, \mathbf{a}))\)되 게 설정하게 된다.

위 업데이트식으로 찾은 행동가치함수는 모든 \((\mathbf{s}, \mathbf{a})\)에 대해서 실제 행동가치함수의 lower bound가 된다는 것이 논문에 증명되어 있다 (Theorem 3.1).


그런데 위 업데이트식은 조금 억울하다. 그냥 \(Q(\mathbf{s}, \mathbf{a})\)의 크기를 막 줄여 버리는 느낌이다. Offline RL에서 더욱 문제가 되는 overestimation은 데이터셋에 없는 상태-행동 순서쌍에 대한 overestimation이다. 따라서, 데이터셋에 있는 상태-행동 순서쌍에 대한 행동가치함수는 다시 높여주는 텀을 추가해준다.

(1)#\[\begin{split} \hat{Q}^{k+1} \leftarrow \operatorname*{argmin}_{Q} \alpha \left(\mathbb{E}_{\mathbf{s}\sim\mathcal{D}, \mathbf{a}\sim\mu(\cdot|\mathbf{s})}\left[ Q(\mathbf{s}, \mathbf{a}) \right] \textcolor{blue}{- \mathbb{E}_{\mathbf{s}\sim\mathcal{D}, \mathbf{a}\sim \hat{\pi}_\beta(\cdot|\mathbf{s})} \left[ Q(\mathbf{s}, \mathbf{a})\right]} \right) \\ + \frac{1}{2} \mathbb{E}_{\mathbf{s}, \mathbf{a} \sim \mathcal{D}} \left[ \left( Q(\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^{\pi}\hat{Q}^k(\mathbf{s}, \mathbf{a}) \right)^2\right], \end{split}\]

여기서 \(\hat{\pi}_\beta(\mathbf{a}|\mathbf{s})\)는 데이터셋에서 빈도를 세서 만든 empirical 정책이다. 데이터셋 \(\mathcal{D}\)에서 \((\mathbf{s}, \mathbf{a})\)가 등장한 횟수를 상태 \(\mathbf{s}\)가 등장한 횟수로 나눠서 확률을 부여하는 확률분포이다. \(\mu(\mathbf{a}|\mathbf{s})\)를 따라서 행동가치함수 값을 낮춰주되 \(\hat{\pi}_\beta(\mathbf{a}|\mathbf{s})\)을 따라서 행동가치함수를 올려주는 방식으로 행동가치함수를 찾게 된다.

위 업데이트식을 사용하여 찾은 행동가치함수을 경우, 행동가치함수의 기댓값인 상태가치함수가 실제 상태가치함수의 lower bound가 되게 된다. 그리고 실제 상태가치함수와 더 가까운 tighter한 lower bound가 된다 (Theorem 3.2).


2.2 Conservative Q-Learning for Offline RL#

사실 2.1 Conservative Off-Policy Evaluation의 내용들은 행동 정책이 만든 데이터셋으로부터 어떤 타겟 정책의 행동가치함수를 추정하는 off-policy evaluation 방법이기 때문에 굳이 offline RL에 국한된 이야기는 아니다. 저자는 위 policy evaluation 방법을 off-policy learning에 사용해도 된다고 말한다.

그러면 어떻게 위의 policy evaluation을 policy optimization에 이용할 수 있을까? 일반적인 policy iteration은 다음 두 과정을 반복한다.

  • Policy evaluation: 현재 정책 \(\pi_k\)의 행동가치함수 \(Q^{\pi_k}\)를 추정

  • Policy improvement: 현재 행동가치함수 \(Q^{\pi_k}\)를 증가시키는 방향으로 정책 업데이트

식 (1)의 최적화 문제를 풀어서 행동가치함수를 구하고, 또 다시 이를 최대화하는 정책을 찾는 방식으로 정책을 업데이트하면 시간이 많이 걸릴 것이다. 한편, Actor-critic 알고리즘에서는 Q-network를 최대화하는 방향으로 정책이 업데이트된다. 이와 유사하게 현재 행동가치함수를 최대화하는 \(\mu(\mathbf{a}|\mathbf{s})\)를 찾아주는 텀을 추가하여 정책과 행동가치함수를 동시에 최적화하는 문제를 생각해볼 수 있다.

\[\begin{split} \min_{Q} \textcolor{blue}{\max_{\mu}} \alpha \left(\mathbb{E}_{\mathbf{s}\sim\mathcal{D}, \textcolor{blue}{\mathbf{a}\sim\mu(\cdot|\mathbf{s})}}\left[ Q(\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{s}\sim\mathcal{D}, \mathbf{a}\sim \hat{\pi}_\beta(\cdot|\mathbf{s})} \left[ Q(\mathbf{s}, \mathbf{a})\right] \right) \\ + \frac{1}{2} \mathbb{E}_{\mathbf{s}, \mathbf{a} \sim \mathcal{D}} \left[ \left( Q(\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^{\pi}\hat{Q}^k(\mathbf{s}, \mathbf{a}) \right)^2\right] + \textcolor{blue}{\mathcal{R}(\mu)}, \end{split}\]

여기서, \(\mathcal{R}(\mu)\)는 정책에 대한 regularizer이다. 어떤 regularizer를 사용하느냐에 따라 최적화 문제가 달라지기 때문에 위의 최적화 식을 \(\text{CQL}(\mathcal{R})\)이라고 명명하였다. 보통 강화학습에서는 정책 \(\mu\)이 너무 확확 업데이트되는 것을 싫어한다. 그래서 주로 특정 분포 \(\rho\)와 너무 멀어지지 않도록 제약을 주고 정책을 업데이트한다. 제약은 주로 KL divergence로 주기 때문에 \(\mathcal{R}(\mu) = -D_{\text{KL}}(\mu || \rho)\)로 준다. 위의 제약을 사용하면 \(\mu(\mathbf{a}|\mathbf{s}) \propto \rho(\mathbf{a}|\mathbf{s}) \cdot \exp(Q(\mathbf{s}, \mathbf{a}))\) 꼴이어야만 한다.


많은 알고리즘에서 \(\rho\)를 이전 정책 \(\hat{\pi}^k\)로 준다. 이 논문에서는 \(\rho\)로 uniform 분포를 주는 경우를 \(\text{CQL}(\mathcal{\mathcal{H}})\)으로 부른다. 어떤 분포와 균등 분포 사이의 KL divergence를 계산하는 것이 해당 분포의 엔트로피를 계산하는 것과 상수배 차이이기 때문이다.

(2)#\[\begin{split} \min_{Q} \alpha \mathbb{E}_{\mathbf{s} \in \mathcal{D}} \left[ \log \sum_{\mathbf{a}} \exp(Q(\mathbf{s}, \mathbf{a})) - \mathbb{E}_{\mathbf{a} \sim \hat{\pi}_{\beta}(\cdot|\mathbf{s})}\left[ Q(\mathbf{s}, \mathbf{a}) \right] \right] \\ + \frac{1}{2} \mathbb{E}_{\mathbf{s}, \mathbf{a}, \mathbf{s}' \sim \mathcal{D}} \left[ \left( Q(\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^{\pi_k}\hat{Q}^k(\mathbf{s}, \mathbf{a}) \right)^2 \right]. \end{split}\]

위 식이 CQL에서 사용하는 Q-network의 업데이트식이다. 정책 \(\mu\) 최대화 텀이 어디 갔는지 궁금할 수도 있다. 사실, \(\max\limits_\mu \left( \mathbb{E}[Q(\mathbf{s}, \mathbf{a})] -D_{\text{KL}}(\mu || \rho) \right)\)을 직접 해석적으로 풀어보면 \(\log \sum_{\mathbf{a}} \exp(Q(\mathbf{s}, \mathbf{a}))\)이 된다. 정책 업데이트 이야기는 식을 유도하기 위함이었고, 사실 여기에는 정책 네트워크가 낄 자리는 없다. 그래서 Q-network를 업데이트하기 위해서만 사용된다.


최종적으로 \(\text{CQL}(\mathcal{\mathcal{H}})\)의 수도 코드를 보면 다음과 같다. 수도코드에 있는 Equation 4가 본 글에서의 식 (2)이다.

../../_images/230530_CQL_algorithm.png

Experimental Evaluation#

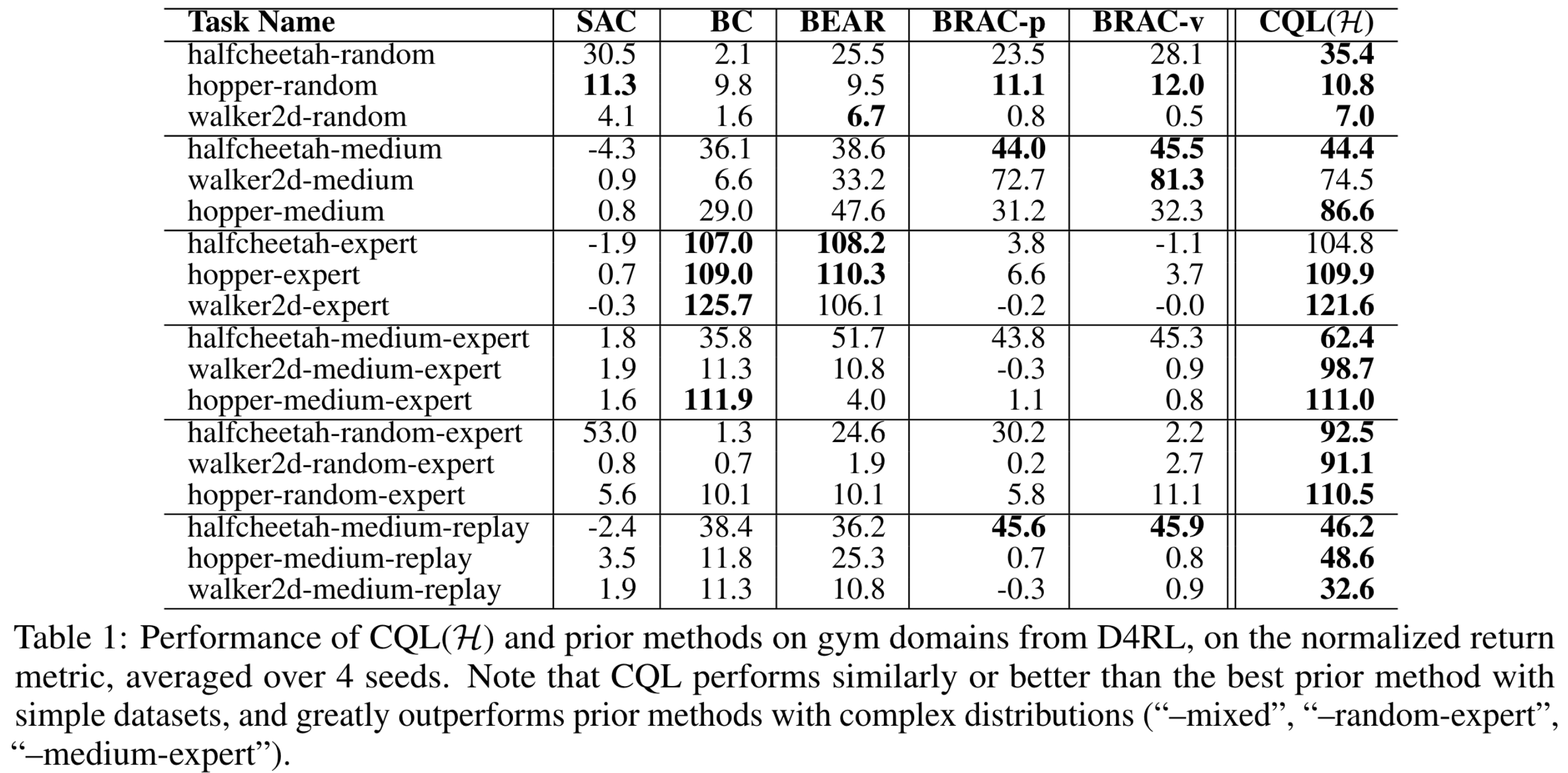
D4RL의 mujoco 도메인에 대한 결과는 아래 표와 같다.

../../_images/230530_cql_result_mujoco.png

마무리하며#

Offline RL 쪽을 연구하고 싶어서 가장 유명한 논문부터 읽어보았다. 수식이 너무 많아서 처음에는 하나도 이해가 안 되었는데, 반복해서 읽다보니 흐름은 잘 이해가 되었다. 본 논문의 꽃은 사실 이론들인데, 아직 이론까지는 정독하지 못해서 본 글에서는 다루지 않았다. 이론 쪽도 읽어 볼 예정이기 때문에 기회가 된다면 이론과 증명을 추가하도록 할 것이다. 빠른 시일 내로 offline RL 실험 환경 구축에 관한 글을 작성할 예정이다.


Reference#

[1] Kumar, Aviral, Aurick Zhou, George Tucker, and Sergey Levine. “Conservative Q-Learning for Offline Reinforcement Learning.” In Advances in Neural Information Processing Systems, 33:1179–91. Curran Associates, Inc., 2020. https://proceedings.neurips.cc/paper/2020/hash/0d2b2061826a5df3221116a5085a6052-Abstract.html.