Encouraging Loss#

  • 제목: Well-Classified Examples Are Underestimated in Classification with Deep Neural Networks

  • 저자: Zhao, Guangxiang, Wenkai Yang, Xuancheng Ren, Lei Li, Yunfang Wu, Xu Sun, Peking University

  • 연도: 2022년

  • 학술대회: AAAI

  • 링크: https://arxiv.org/abs/2110.06537

  • 키워드: Cross-entropy loss

1. Introduction#

분류 문제를 풀 때 떠오르는 흔한 상식 중 하나는 다음과 같다.

  • 이미 잘 분류된 데이터보다 잘 분류되지 않은 데이터를 더 학습해야 한다.

  • 결정 경계에서 먼 데이터보다 가까운 데이터를 더 학습해야 한다.

하지만 이 논문에서는 cross-entropy loss를 사용할 경우, 이미 잘 분류된 데이터, 더 정확히는 모델이 높은 confidence로 예측하는 데이터의 손실 함수에 기여하는 정도가 점점 줄어드는 것을 역전파 관점에서 보인다. 그리고 이를 해결하기 위해 이미 잘 분류된 데이터에 보너스를 부여하는 Encouraging Loss (EL)은 제안한다.

참고로, 잘 분류된 데이터와 모델 학습 사이의 관계를 역전파 관점 외에 다른 두 관점으로도 설명을 하지만, 이 리뷰에서는 내게 익숙한 역전파 관점에서만 정리해본다.


2. Exploring Theoretical Issues of CE Loss#

이 논문에서는 우리에게 아주 익숙한 분류 모델을 다룬다. 데이터 \(\mathbf{x}\)에 대해서 뉴럴 네트워크가 출력 logit을 \(f_\theta(\mathbf{x})\)라고 표기한다. 그리고 그 중 \(y\)번 째 원소를 \(f_\theta(\mathbf{x})[y]\)로 표기한다. Logit에 softmax 함수를 씌워서 만든 확률 분포를

\[p_\theta(\mathbf{x})[y]=\operatorname{softmax}(f_\theta(\mathbf{x}))[y]=\frac{\exp (f_\theta(\mathbf{x})[y])}{\sum_{y'}\exp (f_\theta(\mathbf{x})[y'])},\]

으로 표기한다.


\(p_{\theta}(\mathbf{x})[y]\)를 \(f_\theta(\mathbf{x})[y]\)에 대해서 그레디언트를 구하면 다음과 같다.

\[\frac{\partial \,p_{\theta}(\mathbf{x})[y]}{\partial \, f_{\theta}(\mathbf{x})[y]} = p_{\theta}(\mathbf{x})[y] ( 1- p_{\theta}(\mathbf{x})[y]).\]

한편, 두 이산 확률 분포 \(p\)와 \(q\)의 cross-entropy는 다음과 같이 정의된다.

\[\operatorname{CE}(p, q):=\sum_{x \in \Omega} p(x)\log q(x).\]

분류 모델 훈련시, 확률 분포 \(p\)는 정답 클래스에만 확률 1이고 나머지는 확률이 0이다. \(q\)에 모델이 출력한 확률 분포 \(p_\theta\)을 대입해서 간소화하면 다음과 같다.

\[\operatorname{CE}(p, q):= \log p_\theta(\mathbf{x})[y].\]

Cross-entropy에 마이너스를 붙인 손실 함수를 최적화하여 구한 파라미터는 negative log-likelihood estimation과 동일하다.

\[\mathcal{L}_{\text{NLL}} := - \log p_\theta (y | \mathcal{x})= \log p_\theta(\mathbf{x})[y].\]

\(\mathcal{L}_{\text{NLL}}\)을 \(p_\theta(\mathbf{x})[y]\)에 대해서 미분하면 다음과 같다.

\[\frac{\partial \, \mathcal{L}_{\text{NLL}}}{\partial \, p_{\theta}(\mathbf{x})[y]} = -\frac{1}{p_{\theta}(\mathbf{x})[y]}.\]

지금부터 별다른 언급이 있지 않으면 데이터 \(\mathbf{x}\)에 대한 정답 레이블 \(y\)에 대해 모델이 출력한 확률 \(p_{\theta}(\mathbf{x})[y]\)을 간단히 \(p\)라고 표기할 것이다. 이 논문에서는 \(\partial \mathcal{N}/\partial p=-\frac{1}{p}\)를 steepness of loss라고 정의하였다. \(p\)가 작을수록 손실함수에 대한 미분값이 크기 때문에 잘못 예측된 데이터일수록 손실 함수에 더 크게 관여하게 된다.


한편, 손실함수의 파라미터 \(\theta\)에 대한 그레디언트는 연쇄 법칙에 의하여 다음과 같이 계산된다.

\[\frac{\partial \mathcal{L}_{\text{NLL}}}{\partial \theta}=\frac{\partial \mathcal{L}_{\text{NLL}}}{\partial p}\frac{\partial p}{\partial f_\theta (\mathbf{x})}\frac{\partial f_\theta (\mathbf{x})}{\partial\theta}=(p-1) \frac{\partial f_\theta (\mathbf{x})}{\partial\theta}.\]

\(p\)값이 클수록, 즉 모델이 확신을 갖고 예측할수록, 파라미터에 대한 그레디언트가 0이 된다. 따라서 잘 분류된 데이터일수록 모델 파라미터 업데이트에 기여하지 않게 된다.


3. Method#

위에서 관찰한 내용을 바탕으로 이 논문에서는 잘 분류된 데이터에 보너스 점수를 주는 Encouraging Loss (EL)을 제시한다. 간단하다.

\[\mathcal{N}_{\text{EL}}=- \log p_{\theta}(\mathbf{x})[y] + \log (1-p_{\theta}(\mathbf{x})[y]).\]

\(\log (1-p_{\theta}(\mathbf{x})[y])\) 항을 보너스 항이라고 부른다. \(p_{\theta}(\mathbf{x})[y]\)가 1에 가까울수록 보너스 항이 \(\log 0\)에 가까워져 손실함수가 훨씬 감소하게 된다. 개인적인 생각으로는 이 손실함수를 사용하면 모델의 예측값이 훨씬 극단적으로 1에 가까워질 것 같다. Overconfident한 모델로 수렴할 수 있지 않을까 싶다. \(p\) 값에 따른 EL 손실의 양상을 나타내면 다음 그림과 같다.

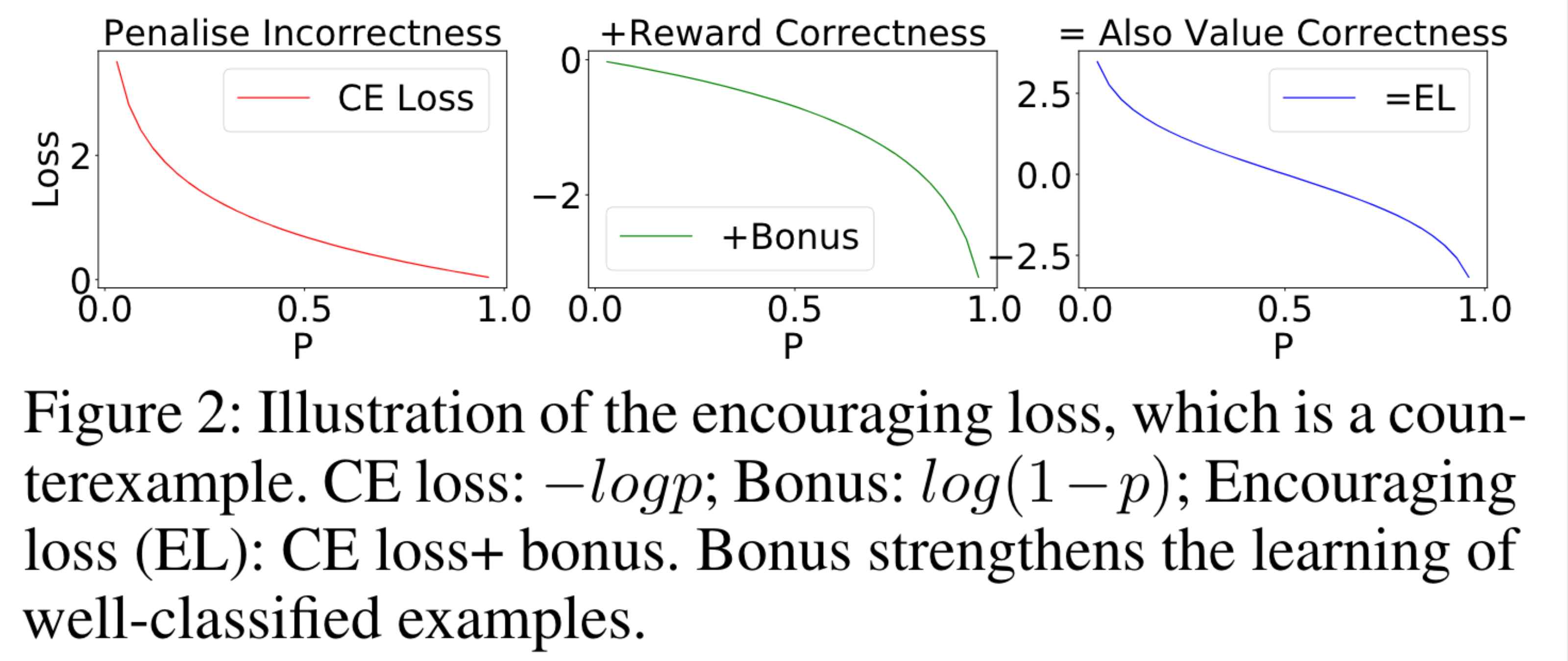
../../_images/230425_el_el.png

Fig. 3 .#


이 손실함수의 좋은 점이 파라미터에 대한 그레디언트가 다음과 같이 더 이상 \(p\)에 의존적이지 않게 된다. 따라서 데이터를 얼마나 확신을 갖고 예측했느냐에 상관 없이 모델 파라미터 업데이트에 기여할 수 있게 된다.

\[\frac{\partial \mathcal{L}_{\text{EL}}}{\partial \theta}=-1 \cdot \frac{\partial f_\theta (\mathbf{x})}{\partial\theta}.\]

한편, Fig. 3의 두 번째 그림이 보여주는 것처럼 \(p\)가 1에 가까워질수록 보너스 항이 음의 무한대에 가까워지게 된다. 이를 방지하기 위하여 기존 보너스 항의 완화된 형태인 conservative bonus 항도 제안하고 있다. Conservative bonus 항은 \(p\)의 값이 정해진 \(LE\)보다 작을 경우 기존 \(\log (1-p)\) 보너스를 갖고, \(LE\)보다 클경우 \(p=LE\)에서의 \(\log (1-p)\)의 접선에 해당하는 보너스를 갖게 된다. 참고로 LE는 Log Ends, 즉 로그가 끝나는 점이라는 의미이다. LE 값에 따른 conservative bonus의 양상은 다음과 같다.

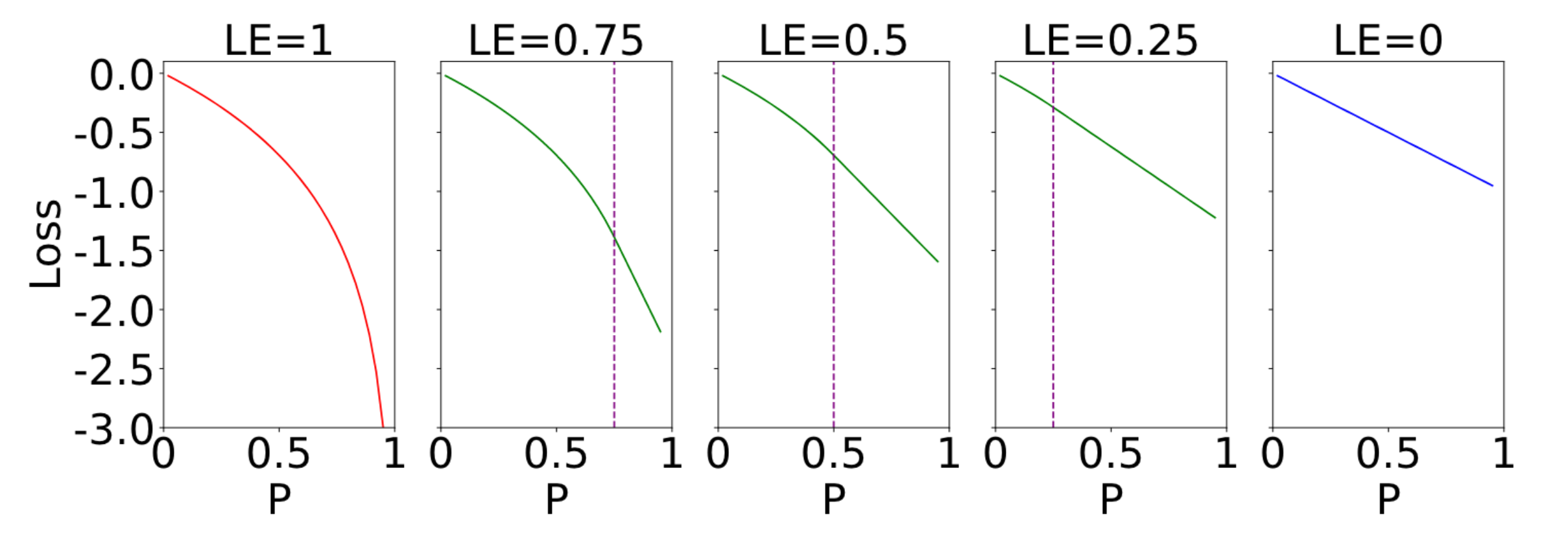
../../_images/230425_el_conservative.png

Conservative bonus를 포함한 손실 함수 Conservative Encouraging Loss (CEL)를 굳이 굳이 적어보면 다음과 같다.

\[\begin{split}\mathcal{N}_{\text{CEL}}= \begin{cases} -\log p + \log (1-p) & p \le LE. \\ -\log p - \frac{p - LE}{1 - LE} + \log(1 - LE) & p > LE. \end{cases}\end{split}\]

4. 실험 결과#

수행한 실험은 다음과 같다.

  • Image Recognition CIFAR10, CIFAR100, ImageNet을 ResNet50과 EfficientNet-B0으로 훈련

  • Graph Classification PROTEINS, NCI1을 GCN으로 훈련

  • Machin Translation De-En, Fr-En을 Transformer로 훈련

다양한 LE 값에 대해서 실험을 진행하였으며, 각 테스크별 가장 좋은 LE 값에 대한 결과는 다음과 같다. 베이스라인 모델들이 제공하는 하이퍼파라미터와 똑같은 하이퍼파라미터를 사용했는데도, 성능 향상이 꽤 있는 편이다.

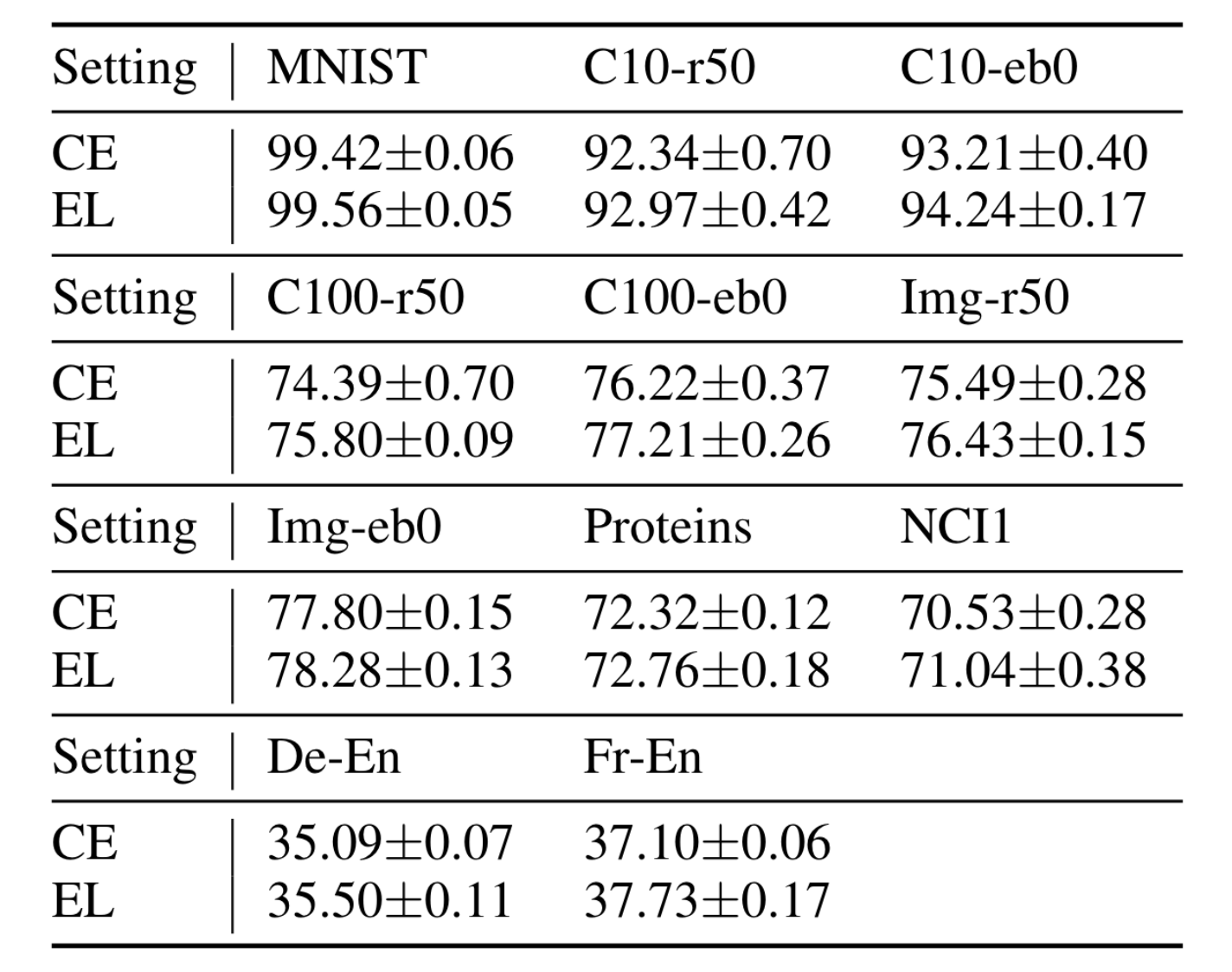
../../_images/230425_el_result1.png

다양한 LE에 대해서 수행한 실험 결과는 다음과 같다.

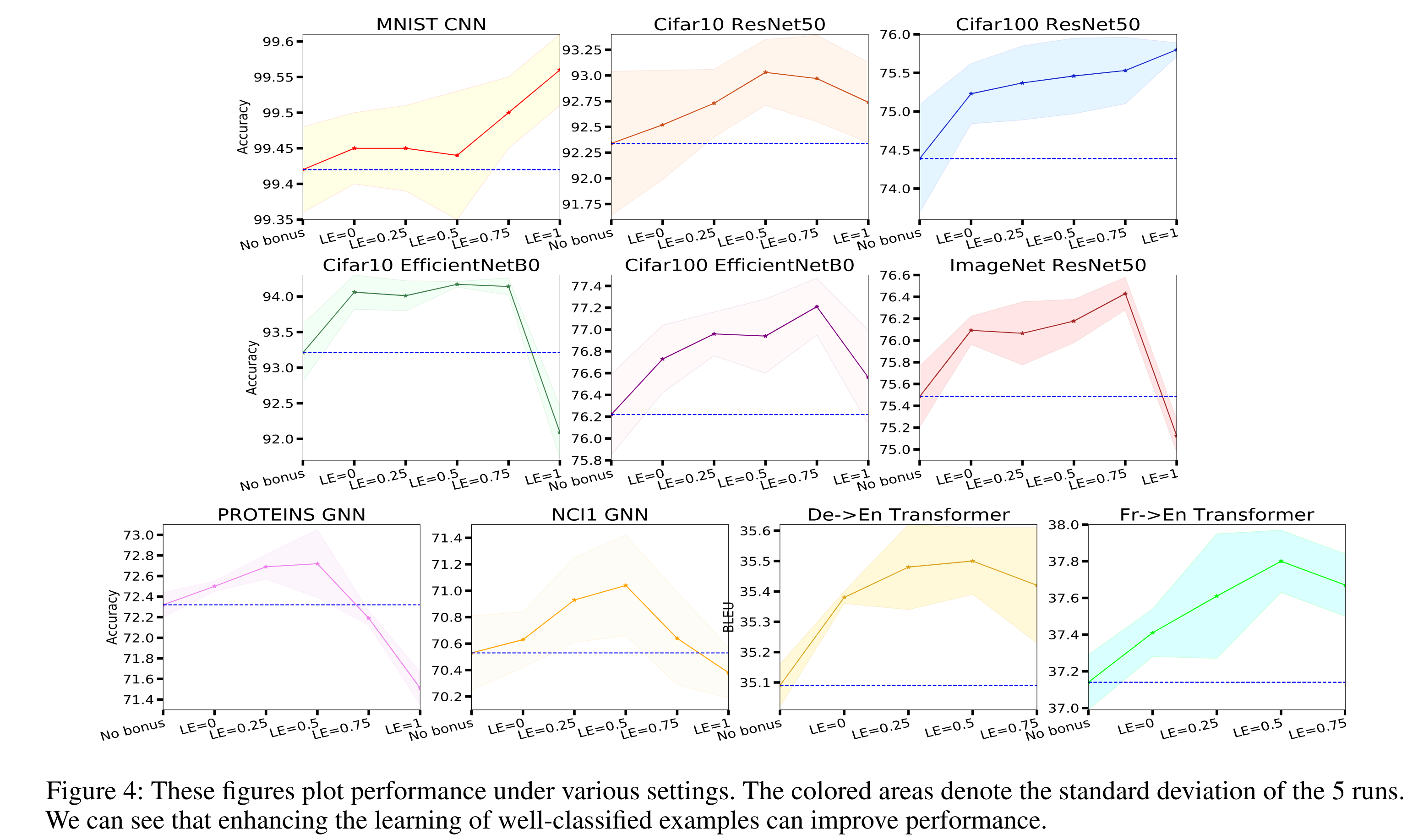
../../_images/230425_el_result2.png

CE의 그레디언트에 \((p-1)\)이 포함되어 있기 때문에 학습이 진행될수록 그레디언트의 크기가 작아져서, learning rate가 감소하는 효과가 있다. 하지마 EL는 그레디언트에 \(p\)텀이 제거되어서 CE와 비교했을 때 더 큰 그레디언트 크기를 갖는다. 따라서 베이스라인의 learning rate보다 더 작은 learning rate를 사용하는 것이 좋고, LE가 1이 아니라 0.5와 0.75일 때 더 잘 작동하는 이유라고 한다.


5. 참고문헌#

[1] Zhao, Guangxiang, Wenkai Yang, Xuancheng Ren, Lei Li, Yunfang Wu, and Xu Sun. “Well-Classified Examples Are Underestimated in Classification with Deep Neural Networks.” Proceedings of the AAAI Conference on Artificial Intelligence 36, no. 8 (June 28, 2022): 9180–89. https://doi.org/10.1609/aaai.v36i8.20904.