Uncertainty-aware Label Correction
Contents
Uncertainty-aware Label Correction#
제목: Uncertainty-Aware Learning against Label Noise on Imbalanced Datasets
저자: Huang, Yingsong, Bing Bai, Shengwei Zhao, Kun Bai, Fei Wang, Tencent
연도: 2022년
학술대회: AAAI
키워드: Learning against label noise, Class imbalance, Uncertainty
1. Introduction#
많은 데이터에 레이블링을 하기 위하여 크라우드소싱, 검색 엔진, 자동 레이블링 등을 사용하다 보면 레이블링이 잘못될 수 있다. 이러한 label noise는 모델에 잘못된 정보를 전달하기 때문에 모델의 성능에 악영향을 미친다. 학습 동안에 noisy label을 찾아내고, 손실함수 또는 레이블을 수정하여 학습하는 방법을 noise-robust learning 이라고 한다.
많은 noise-robust learning 알고리즘들은 뉴럴 네트워크의 memorization effect [2] 성질로부터 아이디어를 얻었다. 뉴럴 네트워크는 학습 초기에는 올바르게 레이블링된 데이터의 패턴을 학습하고, 이후에 점점 잘못 레이블링된 데이터를 기억한다고 한다. 따라서 학습 초기에 손실값이 작은 데이터를 clean 데이터로 간주한다. Clean 데이터와 noisy label 데이터의 손실함수의 분포가 다르다는 점을 이용한 것이다. 기존 방법론들은 성공적이었지만, class imbalance가 있을 경우 작동하지 않을 수 있다. Clean한 데이터라도 major class의 데이터와 minor class의 데이터의 손실함수의 분포가 다르기 때문이다. 따라서, 손실함수 분포의 차이가 class imbalance에 의한 것인지, noise label에 의한 것인지 알 수 없다.
한편, 모델의 예측에는 2가지 불확실성이 있다. Epistemic uncertainty와 aleatoric uncertainty이다. aleatoric uncertainty은 데이터의 노이즈 때문에 발생하는 어쩔 수 없이 발생하는 불확실성이다. Label noise가 포함되어 있다면 aleatoric uncertainty가 발생한다. 한편, 모델 자체의 inductive bias나 over/underfitting 등에 의해 발생하는 불확실성을 epistemic uncertainty라고 한다. 주어진 데이터에 대한 모델의 예측값에 불확실성이 epistemic uncertainty인지 aleatoric uncertainty인지 구별할 수 있어야 한다.
이 논문에서는 uncertainty를 고려하여 class imbalance에서 잘 작동하는 noise correction 방법론인 Uncertainty-aware Label Correction (ULC)을 제시한다.
2. Rethinking Label Correction Framework#
이번 섹션에서는 기존의 label correction 방법론들이 class imbalance 세팅에서 왜 잘 작동하지 않는지 empirically 알아본다.
2.1 Class imbalance 데이터의 손실의 분포#
논문 [3]에 따르면, 뉴럴 네트워크의 classifier층의 파라미터의 norm은 각 클래스의 데이터 개수와 상관 관계가 있다고 한다. 즉, majority 클래스에 대한 노드로 연결된 파라미터들은 큰 스케일을 갖고, minority 클래스에 대한 노드로 연결된 파라미터들은 작은 스케일은 갖는다는 것이다. 따라서, majority 클래스의 데이터는 큰 logit을 갖고 작은 loss를 가지며, minority 클래스의 데이터는 작은 logit을 갖고 큰 loss를 갖는다고 한다. 즉, 클래스별로 손실의 분포가 달라지게 된다.
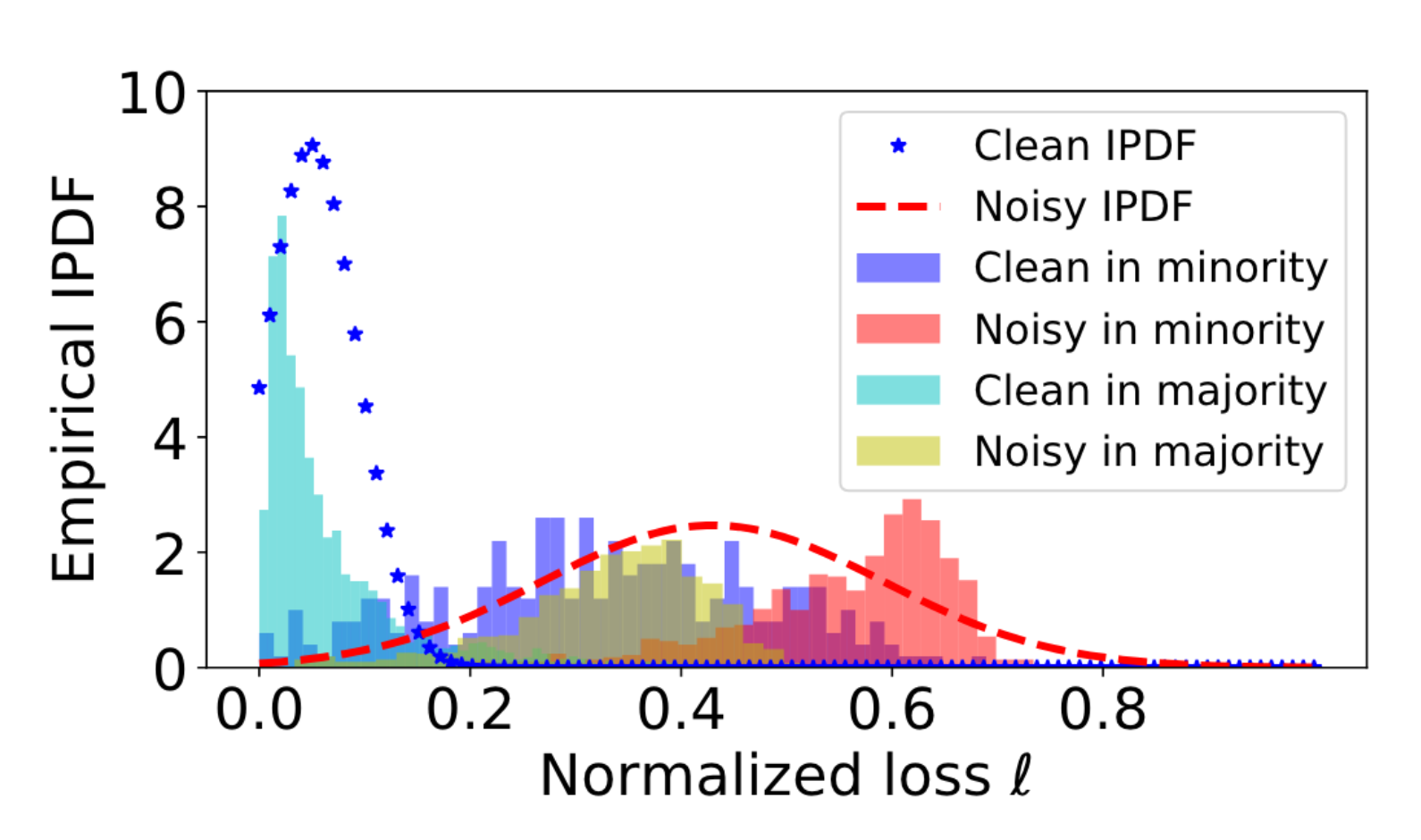
Fig. 1 Inter-class loss distribution discrepancy#
위 그림에서 사용된 실험에 대한 설명은 잠깐 미뤄두고, 그림만 해석해보자. 전체 데이터를 클래스별로 clean 데이터와 noisy 데이터로 나눈 후 손실의 히스토그램을 그려보면 파스텔 색상의 히스토그램들이 나오게 된다. Majority 클래스의 noisy 데이터의 손실 분포 (노란색)와 minority 클래스의 clean 데이터의 손실 분포 (파란색)가 겹치게 된다. 만약 클래스를 고려하지 않고 손실 값만으로 noisy 데이터를 색출하려고 하면, minor 클래스의 clean 데이터가 noisy 데이터로 간주될 수 있다. 실제로 클래스 구별 없이 전체 데이터에 대한 손실 히스토그램에 two-component Gaussian Mixture Model (GMM)을 적합시켜 그린 것이 각각 파란색 별과 빨간색 점선 그래프로 나타난다 (individual PDF). Minority 클래스의 많은 clean 데이터들이 noisy 데이터로 분류될 것이다.
참고로 위 그림에서는 CIFAR10 데이터에서 0번 클래스와 3번 클래스의 데이터가 사용됐고, 데이터의 비율은 1:10으로 샘플링되었다. 클래스별로 50%의 데이터가 잘못된 레이블을 갖고 있다 (noisy label이 많은 감이 있다). PreAct ResNet-18라는 네트워크를 30 epochs 학습한 상황이다.
2.2 Epistemic uncertainty에 의한 손실 분포#
위에서 clean 데이터와 noisy 데이터가 갖는 손실 분포가 다르다는 것을 알아보았다. 이제 손실을 기반으로 주어진 데이터가 clean 데이터인지 noisy 데이터인지 분류하면 될 것 같지만, 한 가지 더 고려해야 할 것이 있다. 바로 모델 자체가 갖고 있는 불확실성이다.
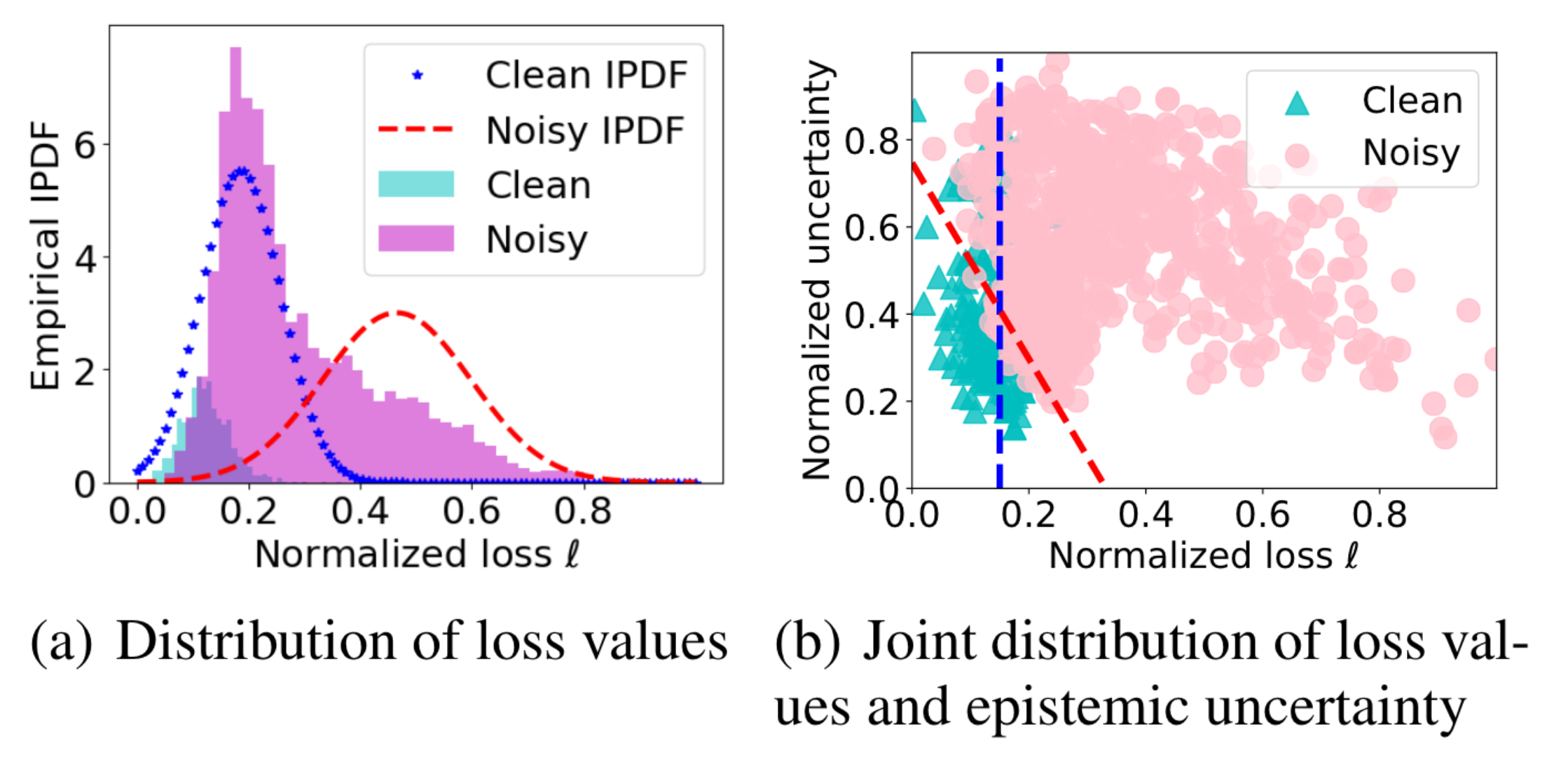
Fig. 2 Effect of epistemic uncertainty#
위의 왼쪽 그림은 90%의 noisy label을 포함한 데이터를 30 epochs 학습된 모델로 손실 값을 구하여 히스토그램을 그린 것이다. 파스텔톤 히스토그램은 clean 및 noisy 데이터의 손실 히스토그램이다. 그리고 파란색 및 빨간색 점선이 GMM으로 노이즈 모델링을 한 것이다. Clean 데이터와 noisy 데이터의 손실 구간이 겹치기 때문에 적합시킨 GMM 또한 clean 영역과 noisy 영역이 많이 겹치게 된다.
위의 오른쪽 그림은 이후 논문에서 epistemic uncertainty와 loss 값 모두를 사용하여 GMM을 적합한 결과이다. 파스텔톤 세모와 네모가 데이터를 의미하고, 파란색 및 빨간색 점선이 적합한 GMM의 각 mode에 대한 결정 경계인 것 같다 (그림에 대한 상세 설명이 부족하다).
3. Method#
기존의 연구들은 각 데이터 \(x_i\)가 clean label을 갖는지 또는 noisy label을 갖는지 분류하기 위하여 데이터의 손실 \(l_i\)를 사용했다. 즉, \(l_i\)가 주어졌을 때, 데이터의 레이블이 clean할 확률 \(p(\tilde{y}_i = y_i^{*}|l_i)\)을 모델링했다. \(\tilde{y}_i\)는 observed label으로 clean할 수도, noisy할 수도 있다. \(y_i^{*}\)는 true label으로 일반적으로 알 수 없다. \(p(\tilde{y}_i = y_i^{*}|l_i)\)은 two-component Gaussian Mixture Model (GMM) 모델링된다. Two-component GMM을 \(\left\{l _i \right\}_{i=1}^{N}\)에 대해 적합시키면 두 모드의 평균 \(\mu_0\)와 \(\mu_1\)이 나오며 (\(\mu_0 \le \mu_1\)), 주어진 손실에 대해 \(p(\mu_0 | l_i)\)가 특정 threshold \(\tau\)를 넘으면 clean 데이터로 간주한다.
이 논문에서는 위 과정에 모델의 epistemic uncertainty \(\epsilon_i\)를 고려하여 clean label 확률 \(p(\tilde{y}_i = y_i^{*}|l_i, \epsilon_i)\)을 모델링한다. 그리고 GMM을 모든 데이터의 손실에 대해서 적합시키는 것이 각 클래스별로 나눠서 적합시키게 된다.
3.1 모델의 Epistemic uncertainty 추정하기#
모델의 epistemic uncertainty를 추정하기 위해서 MC-Dropout을 사용했다고 한다. MC-Dropout은 dropout의 랜덤성을 이용한 것으로, 각 데이터 \(x_i\)를 드랍아웃이 적용된 상태의 네트워크에 \(T\)번 입력시킨다. 드랍아웃이 적용된 상태이기 때문에 똑같은 데이터를 입력하더라도 매번 다른 결과가 나올 것이다. \(T\)개의 예측을 평균 내린 것을 integrated prediction \(\hat{y}_i\)으로 사용한다. 즉,
이때, \(W_t\)는 입력할 때마다 드랍아웃이 적용된 파라미터라고 생각하면 된다. 참고로 실험에서 \(T=10\)이고, 드랍아웃 비율은 \(0.3\)이다. 이렇게 나온 \(\hat{y}_i\)의 엔트로피를 데이터 \(x_i\)에 대한 모델의 epistemic uncertainty \(\epsilon_i\)로 정의했다.
3.2 손실과 epistemic uncertainty를 고려한 clean/noisy 데이터 분류#
데이터 \(x_i\)마다 손실 \(l_i\)와 epistemic uncertainty \(\epsilon_i\)를 구하게 되면, 이제 이를 바탕으로 주어진 데이터 \(x_i\)가 clean label을 가질 확률 \(p(\tilde{y}_i = y_i^{*}|l_i, \epsilon_i)\)을 구해야 한다. 이때, \(l_i\)와 \(\epsilon_i\)가 어떻게 연관되어 있는지 알아내기 어렵기 때문에 논문에서는 독립적이라고 가정했다. 그리고 Fig. 2의 (b)처럼 epistemic uncertainty와 \(p(\tilde{y}_i = y_i^{*}|l_i, \epsilon_i)\)가 negative correlate 되어 있는 것을 실험적으로 알 수 있었다. 이 논문에서는 이 2가지 가정으로 다음과 같이 확률을 모델링했다.
이때, \(p(\tilde{y}_i = y_i^{*}|l_i)\)는 위에서 설명했던 것처럼 two-component GMM이되, 각 클래스별로 적합된 것이다. \(r\)은 하이퍼파라미터로서 실험에서는 \(0.1\)을 사용했다. 이렇게 구한 \(\omega_i\)에 대해서 특정 threshold \(\tau\)를 기준을 넘으면 clean 데이터로 간주하였다. 실험에서는 \(\tau=0.5\) 또는 \(\tau=0.6\)을 사용했다.
3.3 Clean / noisy 데이터 분류 이후 과정#
주어진 데이터 \(x_i\)가 \(\omega_i\)를 기준으로 clean 데이터로 분류되면, 다음과 같이 label을 수정해준다. 레이블로 0 또는 1 같은 극단적인 값을 사용하기 보다는 label smoothing처럼 소수를 사용하여 robust하게 만들기 위함인 것 같다.
이때, \(\tilde{y_i}\)는 observed label이고, \(\hat{y}_i\)은 MC Dropout으로 구한 integrated prediction이다. 그리고 이 데이터는 clean 훈련 데이터셋 \(\tilde{\mathcal{X}}\)에 저장한다
한편, 주어진 데이터 \(x_i\)가 \(\omega_i\)를 기준으로 noisy 데이터로 분류되면, 해당 데이터의 레이블을 아예 없애 버리고 noisy unlabeled 데이터셋 \(\tilde{\mathcal{U}}\) 모아 놓는다.
3.4 Aleatoric Uncertainty-aware Learning#
이 논문에서는 위 과정을 거치고서도 남아 있는 residual noise를 걱정한다. 이 residual noise 때문에 발생한 불확실성을 aleatoric uncertainty로 보고, 이를 완화시킨다. 완화시키는 법은 간단하다. 레이블에 노이즈가 있을 것이기 때문에, 모델의 출력에 노이즈를 추가하여 여러 출력물은 만들고 이를 평균하여 최종 예측을 만들어내는 것이다. 아까 봤던 MC Dropout과 비슷하다.
\(\delta\)와 \(\delta^{x_i}\)는 각각 정규분포 \(\mathcal{N}(0, \sigma)\)와 \(\mathcal{N}(0, \sigma^{x_i})\)에서 샘플링되며, \(\sigma\)와 \(\sigma^{x_i}\) 역시 학습되는 파라미터이다. \(\delta\)와 \(\delta^{x_i}\)를 \(T\)번 샘플링하여 \(T\)개의 corrupted predictions을 만들고, 이를 평균애서 최종 결과물로 사용한다.
3.5 알고리즘#
위의 내용을 바탕으로 이 논문은 다음 2가지를 반복한다.
각 데이터 \(x_i\)의 \(\omega_i\)를 사용하여 clean dataset \(\hat{\mathcal{X}}\)과 unlabeled dataset \(\hat{\mathcal{U}}\)로 나눈다.
Semi-supervised learning을 한다.
손실함수 \(\mathcal{L}=\mathcal{L}_x + \lambda_u \mathcal{L}_u,\) where
지도학습 손실함수 \(\mathcal{L}_x=-\frac{1}{| \hat{\mathcal{X}}|}\sum\limits_{(x_i, y_i) \in \hat{\mathcal{X}}}y_i^\top \log \frac{1}{T}\left( \sum\limits_{t=1}^{T} \hat{y}_i^{(t)} \right),\)
SSL 손실함수 \(\mathcal{L}_u=\frac{1}{\hat{\mathcal{U}}}\sum\limits_{(x_i, y_i) \in \hat{\mathcal{U}}}\lVert y_i - \frac{1}{T} \sum\limits_{t=1}^{T}\hat{y}_i^{(t)}\rVert^2_2.\)
사실 SSL 손실함수에서 \(y_i\)가 어떻게 결정되었는지는 본 논문에는 나와 있지 않은데, DevideMix라는 논문을 따라서 만들어진 것으로 생각된다.
4. 참고문헌#
[1] Huang, Yingsong, Bing Bai, Shengwei Zhao, Kun Bai, and Fei Wang. “Uncertainty-Aware Learning against Label Noise on Imbalanced Datasets.” Proceedings of the AAAI Conference on Artificial Intelligence 36, no. 6 (June 28, 2022): 6960–69. https://doi.org/10.1609/aaai.v36i6.20654.
[2] Arpit, D.; Jastrzebski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M. S.; Maharaj, T.; Fischer, A.; Courville, A. C.; Bengio, Y.; and Lacoste-Julien, S. 2017. A Closer Look at Memorization in Deep Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), 233–242.
[3] Kang, B.; Xie, S. Rohrbach, M.; Yan, Z.; Gordo, A.; Feng, J.; and Kalantidis, Y. 2020. Decoupling Representation and Classifier for Long-Tailed Recognition. In The 8th International Conference on Learning Representations (ICLR 2020)
