Elementary Folklore Construction#

Universal Approximation Theorem 시리즈 1탄. 딥러닝을 공부하는 사람이라면 한번쯤 Universal Approximation Theorem (UAT)을 들어보았을 것이다. 그리고 내용도 어렴풋이라도 알고 있을 것이다. 다층 퍼셉트론으로 이 세상의 모든 함수를 근사할 수 있다는 정도의 내용으로 알고 있을 것이다. 하지만, UAT의 정확한 statement나 증명까지 아는 사람은 거의 없을 것이다. 그도 그럴 것이 정말 많은 버전의 UAT가 있기도 하고, 증명도 복잡할 뿐만 아니라, 사실 몰라도 딥러닝을 사용하는데 큰 문제가 되지 않기 때문이다.

그래도 엄연히 인공지능대학원에서 학위 과정을 밟고 있는데, UAT를 알고 있으면 좋을 것 같아서 이를 공부해서 정리해볼 예정이다. 워낙에 내용이 많을 것 같아서 여러 글에 나눠서 적을 예정이다. 많은 내용을 교내의 <딥러닝 이론> 강의를 참고하여 작성했다.

첫 번째 내용은 비전공자도 쉽게 이해할 수 있는 버전이다. 어떠한 Lipschitz 연속 함수가 주어져도 이를 근사할 수 있는 2-layer network가 존재한다는 내용이다.


Elementary Folklore Construction#

다음 proposition에 더 명확한 statement가 담겨있다.

Proposition 1

Let \(f:[0, 1] \rightarrow \mathbb{R}\) be a \(L\)-Lipschitz continuous function and \(\epsilon > 0 be given\). Then, there exists a 2-layer network \(\tilde{f}\) whose hidden layer has \(\lceil \frac{L}{\epsilon} \rceil\) neurons with unit activation function such that

\[\sup_{x \in [0, 1]}|\tilde{f}(x) - f(x)| \le \epsilon.\]

구간 \([0, 1]\)에서 정의된 \(L\)-Lipschitz 연속 함수 \(f\)와 양수 \(\epsilon\)이 주어진 상황이다. 함수 \(f\)는 우리가 근사하고 싶은 타겟 함수이다. \(L\)-Lipschitz 연속 함수는 다음 성질을 만족한다. 구간 \([0 ,1]\)에서 아무 두 숫자 \(x\)와 \(y\)를 잡았을 때, 두 함수값의 차이 \(|f(x) - f(y)|\)가 비상식적으로 크지 않다는 것이다 (또는 기울기가 \(L\)보다 작다로 해석)$

\[| f(x) - f(y) | \le L |x - y|, \quad \forall x, y \in [0, 1].\]

\(\epsilon\)은 우리가 허용할 오차의 크기로서, 0.000001과 같이 아주 작은 양수라고 생각하면 된다. Proposition이 말하는 바는 타겟 함수와 \(\epsilon\)보다 작게 차이나는 2-layer network를 찾을 수 있다는 것이다. 그 network는 \(\lceil \frac{L}{\epsilon} \rceil\) 히든 노드를 가지며, 이때 activation function으로 unit function을 사용한다.


2-layer network는 hidden layer 1개 output layer 1개로 구성된 네트워크이다. 동일한 표현으로 1-hidden layer MLP라고 할 수 있다. 식으로 나타내면 다음과 같다.

\[\tilde{f}(x) = \sum_{i=1}^{m} a_i \sigma(w_i x + b_i).\]
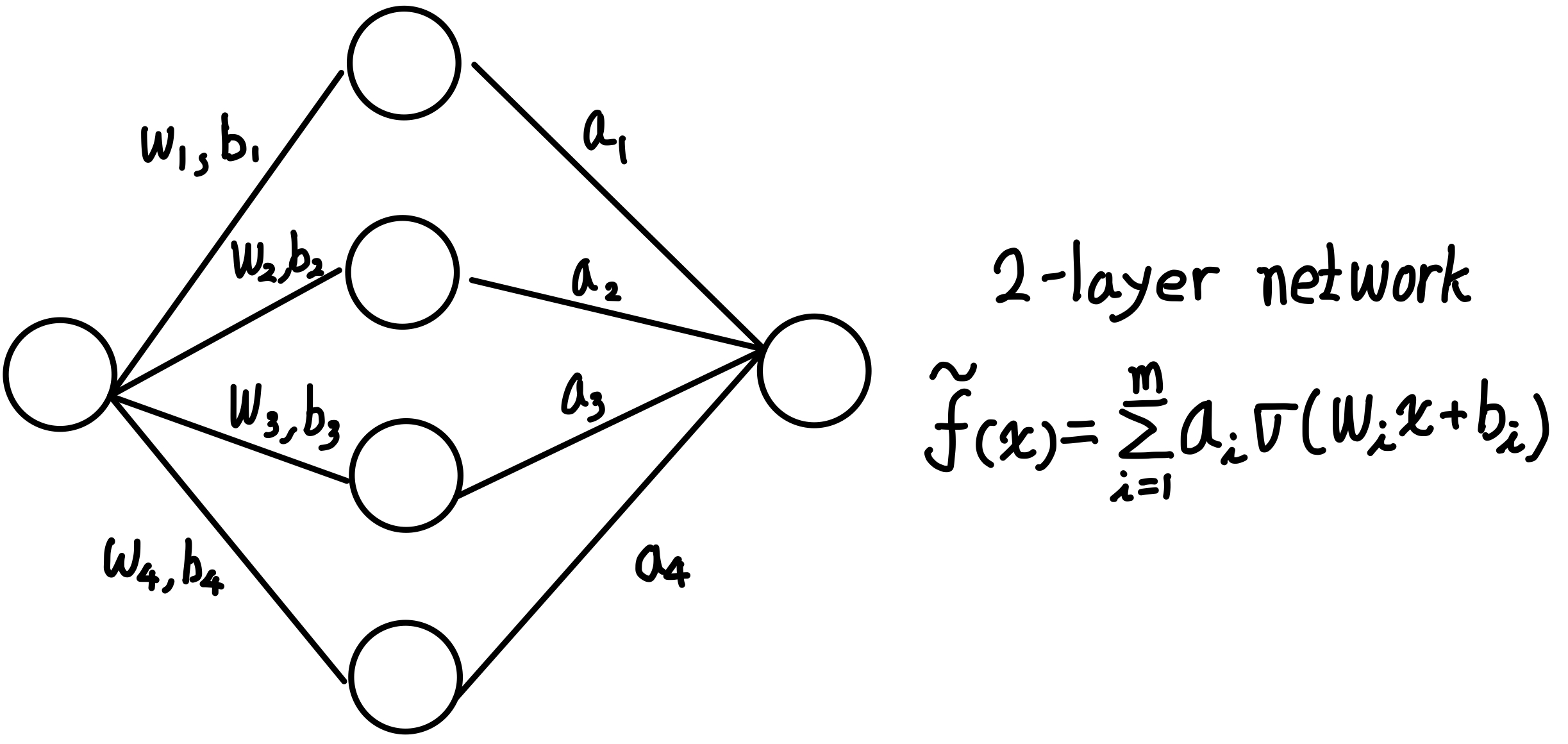
../../_images/230523_network.jpeg

\(w_i\)와 \(b_i\)는 입력층에서 은닉층으로 가는 가중치와 편향이고, \(a_i\)는 은닉층에서 출력층으로 가는 가중치이다. \(\sigma\)는 활성화 함수이며, 여기서는 unit function이다. unit function은 다음과 같이 정의된다.

\[\begin{split}\sigma(z) = \begin{cases} 1 & z \ge 0, \\ 0 & z < 0. \end{cases}\end{split}\]
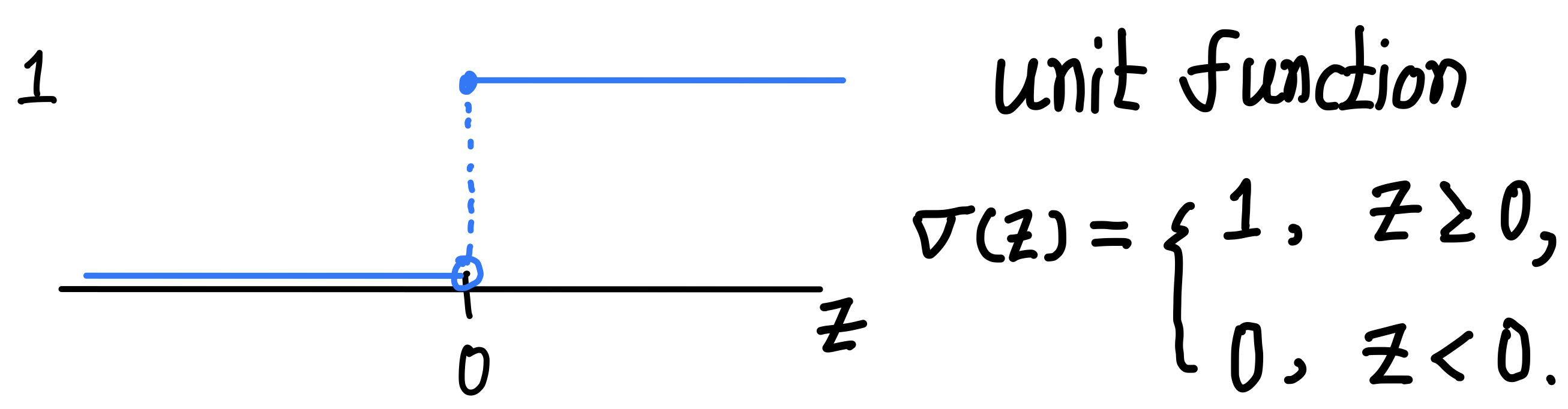
../../_images/230523_unit_function.jpeg

증명#

존재성을 보여야 하는 증명의 경우, 직접 대상을 하나 찾아내는 방식의 by construction 증명을 많이 사용한다. 하나 찾아내도 존재는 하는거니깐.

먼저, \(\epsilon > 0\)이 주어졌다고 하자. 그리고, \(m=\lceil \frac{L}{\epsilon} \rceil\)이라고 하자. 구간 \([0 ,1]\)을 \(m\)등분을 하자. 즉, \(0=b_0 < b_1 < b_2 < \ldots < b_m = 1\)이고 \([b_i, b_{i+1})=[\frac{i\epsilon}{L}, \frac{(i+1)\epsilon}{L})\) for \(i=0, 1, \ldots, m-1\)이다. 다음으로 각 구간의 왼쪽 끝점의 함수값을 높이로 갖는 step function을 \(\tilde{f}\)라고 하자.

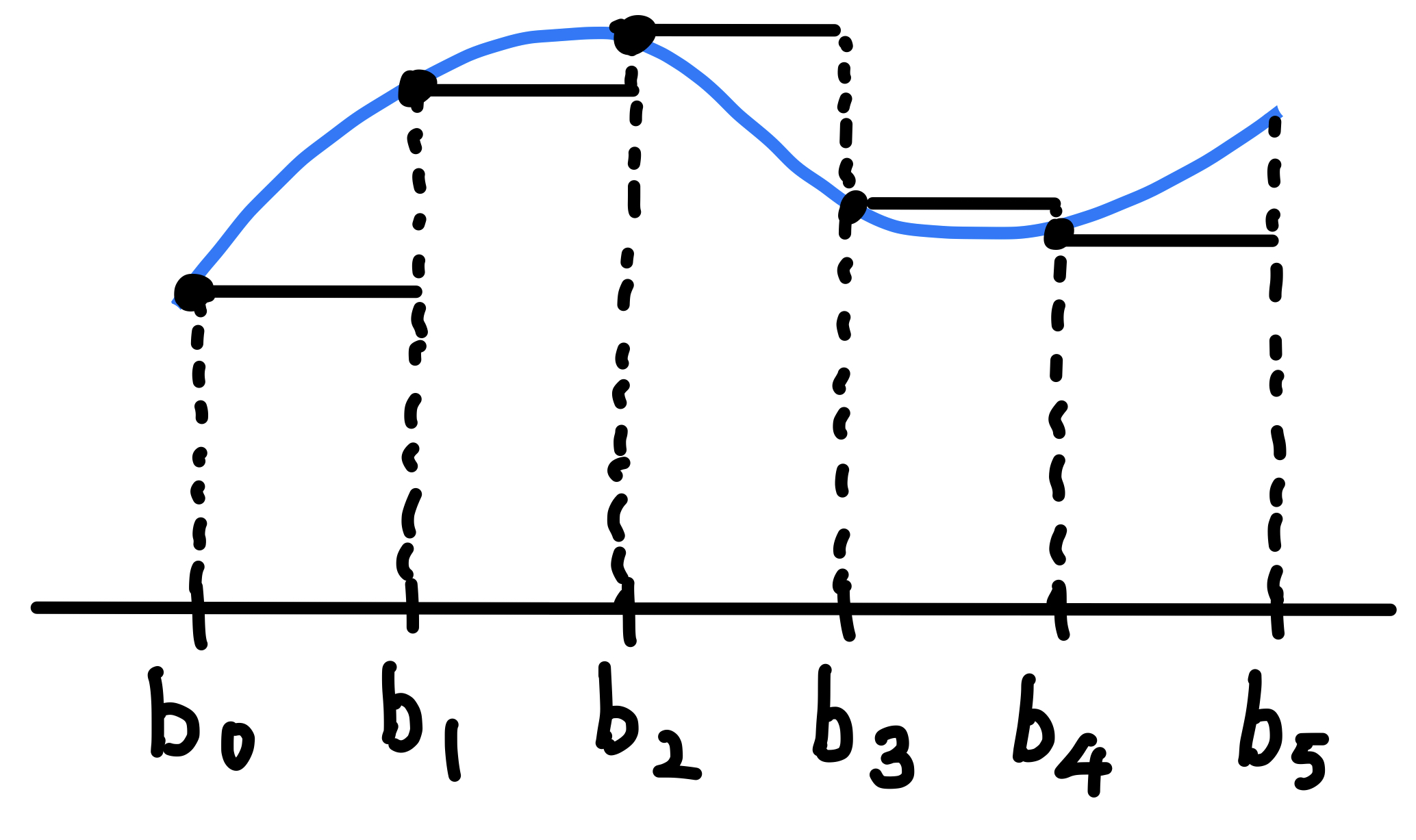
../../_images/230523_step_function.jpeg

예시 그림을 보면 위와 같다. 파란색이 타겟 함수 \(f\)이고 검은색이 우리의 approximator인 \(\tilde{f}\)이다. 지금은 구간 \([0, 1]\)을 5등분 했기 때문에 step function과 타겟 함수가 많이 달라보이지만, 더 잘게 등분할 수록 step function이 타겟 함수에 점점 근사하게 될 것이다.

이 step function을 식으로 표현할 것이다. 이 step function을 unit function들의 합으로 나타낼 것이다.

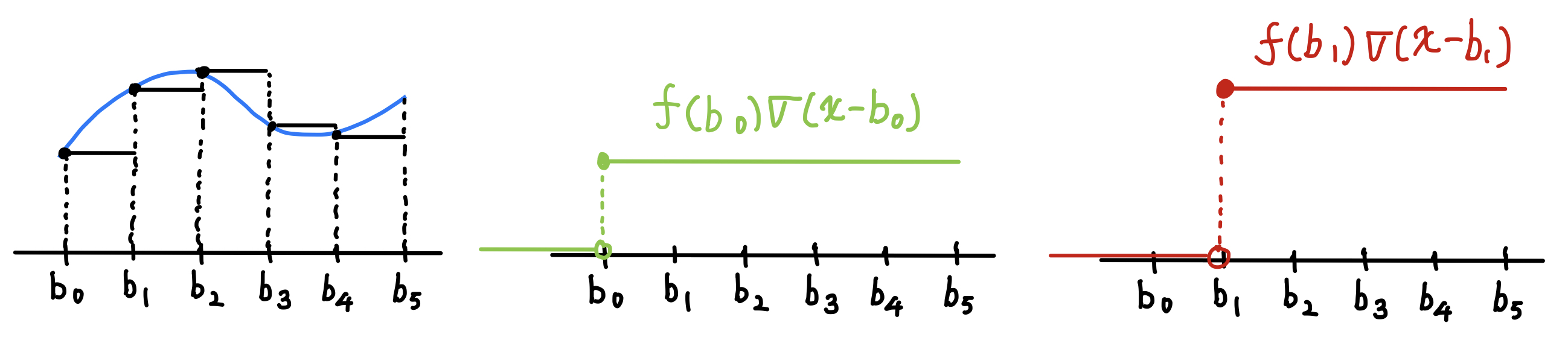
../../_images/230523_unit_functions.jpeg

위 그림의 가운데 그림은 구간 \([b_0, b_1)\)에서의 step function을 만들어내기 위한 unit function이다. unit function이 \(b_0\)만큼 평행이동되었고, \(f(b_0)\)배만큼 스케일링되었기 때문에 해당 unit function의 식은 \(f(b_0) \sigma(x - b_0)\)이다. 오른쪽 그림은 마찬가지로 unit function \(f(b_1) \sigma(x - b_1)\)을 그린 것이다.


이 두 unit functions을 더하면 두번째 구간까지의 step function이 완성될 것 같다. 하지만, 두 unit functions을 단순히 더하면 \(b_1\)부터 step function의 함수값이 \(f(b_0) + f(b_1)\)이 될 것이다. 첫 번째 unit function으로 인해 이미 함수값이 \(f(b_0)\)만큼 있기 때문에 다음으로 더해줘야 할 unit function의 높이는 함수값의 차이인 \(f(b_1) - f(b_0)\)이 되어야 한다. 즉, \(b_1\)부터 함수값이 \(f(b_1)\)이 되기 위해서는 \(f(b_0) \sigma(x - b_0)\)와 \((f(b_1) - f(b_0)) \sigma(x - b_1)\)을 더해줘야 한다.

../../_images/230523_unit_functions2.jpeg

이 과정을 반복해주면 step function \(\tilde{f}\)를 다음과 같이 적어줄 수 있다.

\[\tilde{f}(x) = \sum_{i=0}^{m-1} a_i \sigma(x - b_i).\]

그리고, 이 step function은 다음과 같은 가중치와 편향을 갖는 2-layer network가 수행할 수 있는 연산이다.

  • 입력층\(\rightarrow\)은닉층의 가중치 \(w_i = 1\) for \(i=0, 1, \ldots, m-1\),

  • 입력층\(\rightarrow\)은닉층의 편향 \(b_i = -\frac{i\epsilon}{L}\) for \(i=0, 1, \ldots, m-1\),

  • 히든층\(\rightarrow\)출력층의 가중치 \(a_0 = f(b_0)\), \(a_i=f(b_i) - f(b_{i-1})\) for \(i=1, 2, \ldots, m-1\).


구간 [0, 1] 안의 점 \(x\)에서의 step function과 타겟 함수 \(f\) 사이의 오차를 계산해보자. \(x\)가 속한 구간 \([b_k, b_{k+1})\) for some \(k=0, 1,\ldots, m-1\)을 찾을 수 있을 것이다.

\[\begin{split} \begin{matrix} |f(x) - \tilde{f}(x)| & \le & |f(x) - f(b_k)| + |f(b_k) - \tilde{f}(b_k)| + |\tilde{f}(b_k) - \tilde{f}(x)| \\ & \le & L | x - b_k| + \Big|f(b_k) - \sum\limits_{i=0}^{k}a_i \Big| + 0\\ & \le & L \frac{\epsilon}{L} + \Big| f(b_k) - f(0) - \sum\limits_{i=1}^{k} \left( f(b_i) - f(b_{i-1})\right)\Big| \\ & = & \epsilon. \end{matrix} \end{split}\]

첫 번째 부등식은 triangle inequality에 의해 성립한다. 두 번째 부등식의 첫 번째 텀은 타겟 함수의 \(L\)-Lipschitz 성질에 의해 \(L|x-b_k|\)보다 작게 된다. 세 번째 텀은 step function은 구간 \(b_k \le x < b_{k+1}\)에서 모두 같은 값을 갖기 때문에 0이 된다. 두 번째 텀의 \(\tilde{f}(b_k)=\sum_{i=0}^{m-1} a_i \sigma(x - b_i)\)이다. \(\sigma(b_k-b_i)\)가 \(b_k\)가 \(b_i\)보다 클 때만 1이기 떄문에 \(k\)번 째까지의 \(a_i\)를 더해준 것으로 남게 된다.

세 번째 부등식의 첫 번째 텀은 \(|x-b_k|\)보다 구간 \([b_k, b_{k+1})\)의 길이 \(\frac{\epsilon}{L}\)가 더 크다는 사실 때문이고, 두 번째 텀은 \(a_i\)의 정의를 사용해서 \(\sum_{i=1}^{k}a_i\)를 전개해보면 0이 된다. 따라서 \(x\in[0,1]\)에서의 두 함수의 오차가 \(\epsilon\)보다 작게 된다.

위 사실은 구간 \([0, 1]\) 내 모든 \(x\)에 대해서 성립하므로 다음도 성립한다.

\[\sup_{x \in [0, 1]}|\tilde{f}(x) - f(x)| \le \epsilon.\]

마무리하며#

위 증명을 요약하자면, \([0, 1]\)에서 정의된 임의의 \(L\)-Lipschitz 연속 함수와 임의의 오차 \(\epsilon\)이 주어져도, 그 함수와 \(\epsilon\)만큼만 차이나는 2-layer network가 적어도 하나 존재한다는 것이다. 해당 그 적어도 하나의 2-layer network는 \(\lceil \frac{L}{\epsilon} \rceil\)개의 은닉 노드를 갖으며 활성화 함수로 unit function을 사용한다.

사실, 타겟 함수의 도메인이 1차원이라는 점과 불연속점을 포함하고 있는 unit function을 활성화 함수로 사용한다는 점에서 실용적인 proposition은 아니다. 하지만, 많은 UAT의 증명 과정이 이 proposition의 증명 과정과 유사하다. 먼저 도메인을 작게 나누고, 각 구간마다 동일한 함수값을 갖는 함수를 만들어낸 후, 그 함수가 타겟 함수와 \(\epsilon\)만큼 차이난다는 것을 보인다.

언제 돌아올지는 모르겠지만, 만약 다시 돌아온다면 ReLU 활성화 함수를 갖는 2-layer network로 연속 함수를 근사시키는 이론 정리해볼 것이다.


참고 문헌#

[1] Matus Telgarsky, Deep learning theory lecture notes, 2021. https://mjt.cs.illinois.edu/dlt/