강화학습 용어 백과사전

얼마 전부터 강화학습에 입문하였다. 공부하는 동안 강화학습 용어들이 대체로 추상적이라서 이해하기 어려웠다. 통계 공부할 때 모평균과 표본평균의 차이를 받아들이기 어려웠던 것처럼 말이다. 강화학습을 공부할 때는 모수와 통계량을 잘 구분할 필요가 있다. 강화학습 문제를 기술하기 위한 용어는 대부분 모수라고 생각하면 된다.
강화학습 이해를 방해하는 다른 한 가지 요소는 용어들의 Recursive한 성질이다. 예를 들어, 현재 시점의 Value 값을 구하기 위해서는 미래 시점의 Value 값을 알아야 한다. 그런데 미래 시점의 Value 값을 구하려고 가보면 더 미래 시점의 Value 값을 가져오라고 한다. 마치 무한츠쿠요미에 빠진 것만 같았다. 이를 처음에 받아들이기 어려웠다. 하지만 일단 이 Recursive한 성질을 받아들이기 시작하면 강화학습의 마법이 펼쳐지기 시작한다. (물론 난 아직 이해 못했다.)
이 포스팅에서 나는 지금까지 이해하기 어려웠던 강화학습 용어들에 내 나름대로의 해석을 덧붙여보았다. 단 한 명에게라도 이해를 돕고 공감을 살 수 있다면 난 만족한다.
들어가기 전에
- 이 글은 지속적으로 업데이트 됩니다.
- 원하시는 키워드를
Ctrl+F로 찾아서 선택적으로 읽는 방법을 추천드립니다. - Richard S. Sutton and Andrew G. Barto, Reinforcement Learning: an introduction, 2017의 표기법을 최대한 따랐습니다.
일반적인 표기법 (General notations)
$s$: State
$a$: Action
$\pi$: Policy (정책)
- Policy는 쉽게 말해서 주어진 상태 (state)에서 어떻게 행동 (action)할지 알려주는 지침서이다. 강화학습의 목적은 상황에 맞는 최적의 지침서를 찾는 것이다.
- 만약 이 지침서가 주어진 state에서 취해야 할 action을 딱 하나 정해준다면, 이 지침서를 deterministic policy 라고 부른다. 그리고 $\pi(s)=a$로 표기한다.
- 일반적으로, 주어진 state에서 취할 수 있는 action들이 여러 가지이다. 따라서 이 지침서에는 state $s$ 에서 각 action $a$를 취할 확률이 적혀 있다. 즉, 지침서에는 조건부확률 $P(A_t=a \mid S_t=s)$ 들이 적혀 있으며, 이 조건부확률을 간략하게 $\pi(a \mid s)$로 적어준다. 의미는 주어진 state $s$에서 action $a$를 취할 확률 이다. 주어진 state에서 취할 action을 조건부확률분포에서 샘플링하여 선택하기 때문에 이 지침서를 stochastic policy 라고 부른다.
- 가능한 state와 action 조합이 적을 때는 모든 조합마다 얻을 수 있는 Value function 값을 계산하여 표를 만들어놓는다. 이를 table-lookup 방식이라고 부른다. 메모리에 저장된 표를 보며 action을 선택하는 행위 또한 policy라고 이해할 수 있다.
- 조합의 경우가 너무 많으면 true policy $\pi$를 구하는 대신 매개변수로 표현되는 모델을 사용한다. $\theta$로 매개변수화된 policy는 $\pi_\theta$ 으로 표기한다.
$G_t$: Return
- $G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty{\gamma^k R_{t+k+1}}$
- $t$ 시점 이후로 Policy를 따라 에피소드를 진행했을 때 얻는 보상들의 합 (시간 경과에 따른 discounted 적용)
- 강화학습은 단순히 “현재 state에서 reward 가장 많이 주는 액션을 취하는 것”이 아니다. 미래의 보상까지 고려하는 “Return 값이 가장 높은 액션을 취하는 것”이다.
$v_\pi(s)$: State-value function
- $v_\pi(s)=\mathbb{E}_\pi[G_t \mid S_t=s]$
- 현재 state $s$ 이후로 Policy $\pi$를 따라 에피소드를 진행했을 때 얻게 되는 return의 기댓값
- state $s$ 에서 시작하여 Policy $\pi$를 따라 에피소드를 진행하면 1개의 에피소드가 만들어지고 대응하는 $G_t$ 값이 산출된다. 이 과정을 여러번 반복하면 여러 에피소드와 여러 $G_t$가 만들어질텐데 그것의 평균으로 이해하면 된다. (이 설명은 표본평균에 대한 이야기고, 실제 기대값은 알 수 없는 모수로서 표본평균으로 추정을 한다.)
- 일반적으로 $v_\pi$는 알 수 없는 모수이기 때문에 다양한 방법으로 $v_\pi$ 를 추정하게 된다. $v_\pi$의 추정치는 $V_\pi$로 적어주게 된다.
$q_\pi$: Action-value function
- $q_\pi(s, a)=\mathbb{E}_\pi[G_t \mid S_t=s, A_t=a]$
- 현재 state $s$에서 action $a$를 취한 이후로 Policy $\pi$를 따라 에피소드를 진행했을 때 얻게 되는 return의 기댓값
- state $s$에서 시작하여 action $a$를 취하고 난 이후에 Policy $\pi$ 를 따라 진행하면 1개의 에피소드와 $G_t$ 값이 완성된다. 이 과정을 여러번 반복하여 얻은 $G_t$들의 평균으로 이해하면 된다.
- 일반적으로 $q_\pi$는 알 수 없는 모수이기 때문에 다양한 방법으로 $q_\pi$ 를 추정하게 된다. $q_\pi$의 추정치는 $Q_\pi$로 적어주게 된다.
- state $s$에서 취할 수 있는 action들은 여러가지가 있을 것이다. 각 action $a$에 대한 $q_\pi(s, a)$ 값들의 평균을 구하면 $v_\pi(s)$ 값이 된다. 즉,
$v_\pi(s)=\sum_{a \in A}\pi(a|s){q_\pi(s, a)}$
$\mu^{\pi}(s)$: Stationary distribution
- Policy $\pi$를 따라 에피소드를 진행했을 때, state $s$가 등장할 확률로 이해하면 쉽다.
- 예를 들어 3가지 state $s_1, s_2, s_3$가 있다고 가정하자. Policy $\pi$를 따라서 에피소드를 진행하다보니 $s_1, s_2, s_3$가 각각 70번, 20번, 10번 등장했다고 하자. 그럼 $\mu^{\pi}(s_1)=\frac{70}{100}=0.7$, $\mu^{\pi}(s_2)=\frac{20}{100}=0.2$, $\mu^{\pi}(s_3)=\frac{10}{100}=0.1$이 된다.
$\mathbf{x}(s)$: Feature vector of state $s$
- 사실 state 자체는 구체적이지 않고 모호하다. state는 실수값인가? 혹은 벡터값인가? 그 어떤 설명에서도 “state가 실수이다.” 또는 “state는 벡터다.”라고 기술하지 않는다. $\mathbf{x}(s)$는 이런 모호한 state 를 구체적인 값으로 나타낼 수 있게 해준다. 예를 들어, 슈퍼마리오 게임에서 특정 state에 대한 feature vector를 만들자면
[마리오의 좌표, 적의 좌표, 적과의 거리, ...]가 될 수 있다. feature vector는 다음과 같이 표기할 수 있다.
$\mathbf{x}(s) = \begin{bmatrix}x_1(s) \\ x_2(s) \\ \vdots \\ x_n(s)\end{bmatrix} $
- 각각의 $x_i$ 들은 state로부터 특징을 뽑아내는 함수이다. 예를 들어, 마리오의 좌표를 구해주는 함수, 적의 좌표를 구해주는 함수, 적과의 거리를 구해주는 함수이다.
- state와 $\mathbf{x}(s)$는 엄격하게 구분하지 않고 사용되는 것 같다.
- state $s$에서 가능한 action $a$까지 사용하여 feature vector를 만들 수도 있다. $\mathbf{x}(s, a)$
다양한 agent 분류 기준
off-policy learning: 에피소드를 만들어나가는 Policy (behavior policy)와 학습에 사용되는 Policy (target policy)를 따로 사용하는 학습 방법
- 배경: 우리는 Optimal한 행동들로 이루어진 에피소드를 사용 (
exploitation) 하여 action-value를 추정해야 한다. 하지만, 더 좋은 행동이 있는지 탐색 (exploration) 하기 위해서는 Optimal하지 않은 행동들을 해야 한다. 이와 같은exploration-exploitation dilemma를 해결할 수 있는 가장 직관적인 방법은 2가지 Policy를 사용하는 것이다. 하나의 policy는 optimal policy를 찾기 위해 학습에 사용되며 이를target policy라고 부른다. 다른 하나는 보다 더 탐색적으로 action들을 취하여 데이터를 만들며,behavior policy라고 부른다. target policy를 벗어난 (off) 데이터를 policy 학습에 사용한다고 하여off-policy learning이라고 부른다.In this case we say that learning is from data “off” the target policy, and the overall process is termed off-policy learning.
Target policy에서 벗어난 데이터를 학습에 사용하기 때문에 수렴이 느리고 학습 동안 큰 variance를 가질 수 있다.off-policy learning이 보다 더 포괄적인 개념이라고 할 수 있다.on-policy learning는behavior policy와target policy가 같은 경우라고 해석할 수 있다.
Multi-Armed Bandits (MAB)
강화학습에서 가장 큰 주제 중 하나인 exploration-exploitation dilemma를 이해하기 위한 예시로 많이 등장하는 문제이다. MAB 문제는 다음과 같다.
- 당신 앞에 기대 보상이 서로 다른 슬롯머신 (Bandit)이 여러 개 있다고 상상해보자
- 어떤 슬롯머신이 어느 정도의 보상을 줄지는 모르는 상태에서 시작한다.
- 우리의 목표는 가장 많은 보상을 주는 슬롯머신을 찾아서 (exploration) 그것만 계속 작동시켜 (exploitation) 가장 큰 보상을 챙기고 유유히 사라지는 것이다.
이때, 탐색이 충분하지 않았다면 가장 좋은 슬롯머신 아닌 엄한 슬롯머신을 선택할 위험이 생긴다. 반대로 탐색에 너무 많은 시간을 소비한다면 가장 좋은 슬롯머신을 작동시킬 기회가 줄어들게 된다.
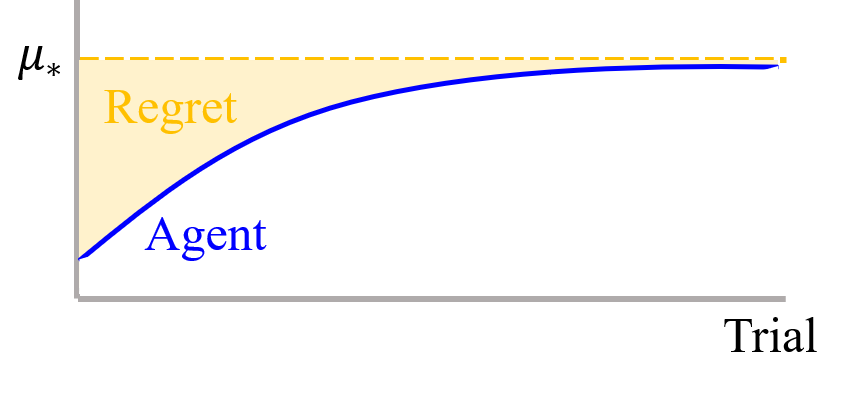
Regret: MAB 문제에서 agent들의 성능을 비교하기 위한 평가지표 중 하나이다. 처음부터 가장 좋은 슬롯머신을 작동시켜 얻을 수 있는 실제 총 reward 값과 agent의 전략에 따라 슬롯머신을 작동시켜 얻은 실제 reward 값의 차이이다. 즉,
$\text{Regret } \mathcal{T}=\mu_*n-\sum\limits_{i=1}^{K}\mu_i\mathbb{E} [T_i(n)] = \sum\limits_{i=1}^K(\mu_{*}-\mu_i)T_i(n)$
이때, 총 $K$개의 슬롯머신이 있으며 $n$번의 시행 (슬롯머신 작동)이 있는 것이다. 그리고 $\mu_*$는 가장 좋은 슬롯머신이 주는 기대 보상이며 $\mu_i$는 $i$번 째 슬롯머신이 주는 기대 보상이다. 마지막으로 $T_i(n)$은 $i$번 째 슬롯머신을 작동시킨 횟수이다. 물론 이 regret은 각 슬롯머신들의 기대 보상 $\mu_i$들을 안다는 가정하에 계산할 수 있다. MAB의 목적은 이 regret을 최소화시키는 것이다. 설명이 복잡했지만 agent의 전략의 기회비용 쯤으로 이해하면 된다.
강화학습 아카이브
사실 이 글을 작성하며 내 지식은 거의 들어가지 않았다. 이 글의 모든 내용은 다음 참고문헌들을 기반으로 작성하였다. 모든 참고문헌 작성자들에게 감사의 인사를 전하고 싶다.
Video
- Video 강화학습의 기초 이론, 팡요랩
Reading Material
- Slide Introduction to Reinforcement Learning with David Silver
- Book Richard S. Sutton and Andrew G. Barto, Reinforcement Learning: an introduction, 2017
- Book Grokking Deep Reinforcement Learning
- Paper Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D. & Riedmiller, M.. (2014). Deterministic Policy Gradient Algorithms. Proceedings of the 31st International Conference on Machine Learning, in PMLR 32(1):387-395

