
1줄 요약: Actor Critic + Off policy + Soft policy improvement w.r.t entropy = SOTA
- 제목: Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
- 저자: Haarnoja, Tuomas, Aurick Zhou, Pieter Abbeel, Sergey Levine, Berkeley AI Research
- 연도: 2018
- 링크: https://proceedings.mlr.press/v80/haarnoja18b.html
논문이 해결하고자 한 것
- On policy 방법론들은 sample inefficient 하다 → 그럼 Off policy 사용하자!
- Off policy 방법론들은 하이퍼파라미터에 robust하지 않고, 훈련이 instable하다 → 그럼 maximum entropy 기법 사용하자!
사전지식
내가 강화학습 공부를 시작하고 얼마 지나지 않았을 때 이 논문을 읽었다. 어떤 분야의 SOTA 논문을 읽으면, 해당 분야가 어떻게 흘러가고 있는지 알 수 있을 것이란 믿음 때문이었다. 하지만 이 논문은 강화학습 분야의 여러 기술들의 집약체이었기 때문에 이해하기가 너무 어려웠다. 강화학습을 조금 공부한 후에 이 논문을 다시 읽으니 그래도 이전보다는 이해가 잘 되었다. 나같은 강린이분들을 위하여 논문 이해를 위한 사전지식에 대해 적어본다.
On-policy vs. off-policy
On-policy 기법은 에이전트가 현재 정책을 기준으로 환경과 직접 상호작용하여 데이터를 수집하고, 그때 그때 정책 및 가치 네트워크를 업데이트해나가는 기법이다. 환경과 한 번 상호작용하여 얻은 데이터 $(s, a, r, s’)$로 네트워크들을 업데이트할 수도 있고, 특정 횟수만큼 상호작용 후 업데이트할 수도 있다. 여기서 중요한 점은 한 번 업데이트에 사용된 데이터는 버려진다는 것이다. 업데이트된 정책은 더 이상 현재 정책이 아니기 때문이다. 수집한 데이터를 재활용하지 않고 업데이트하는 데 한 번만 사용하기 때문에 sample inefficient하다. PPO, TRPO 등이 on policy에 속한다.
Off-policy 기법은 환경과 상호작용하면서 데이터를 수집하는 정책 (behavior policy)과 업데이트 대상이 되는 정책 (target policy)이 다른 기법을 말한다. 극단적인 예로는 모든 상태에 대해서 임의의 행동을 취하는 정책으로 데이터를 수집하고, 그 데이터를 사용해서 최적의 정책 (타겟 정책)을 찾아나간다. 임의로 행동을 취하면서 어떤 행동을 했을 때 큰 보상을 주고 어떤 행동을 했을 때 낮은 보상을 주는지 알 수 때문이다. Off policy 기법은 수집한 데이터를 여러번 사용하기 때문에 상대적으로 sample efficient하지만, 좋은 정책을 찾기까지 오랜 시간이 소요된다. DQN, DDPG 등이 off policy에 속한다.
Off policy, 비선형 function approximation, bootstrapping을 함께 사용하면 학습이 많이 불안정해지고 하이퍼파라미터 설정에 민감해지는데, 이를 deadly triad라고 부른다.
엔트로피
엔트로피는 확률 분포에 대해 정의되는 값이다. “어떤 확률 분포의 엔트로피는 몇이다.” 라고 말하는 것이다. 사실 어떤 random variable에 대해 정의되는 것인데, 확률 분포에 정의한다고 생각하시는 것이 이해하기 좋다. 어떤 확률 분포 $p(x)$의 엔트로피는 다음과 같이 정의된다. 참고로 두 번째 등호는 이산확률변수일 때 기대값의 정의이다. \[\mathcal{H}(X)=\mathbb{E}\left[-\log p(X) \right]=-\sum_{x \in \mathcal{X}} p(x)\log p(x).\]
무엇을 의미하는지 전혀 감도 안 오지 않는다. 직관적으로 말하자면 엔트로피는 불확실성이다. 그럼 확실한 분포는 무엇이고, 불확실한 분포는 무엇일까? 다음 그림을 보자. 출처
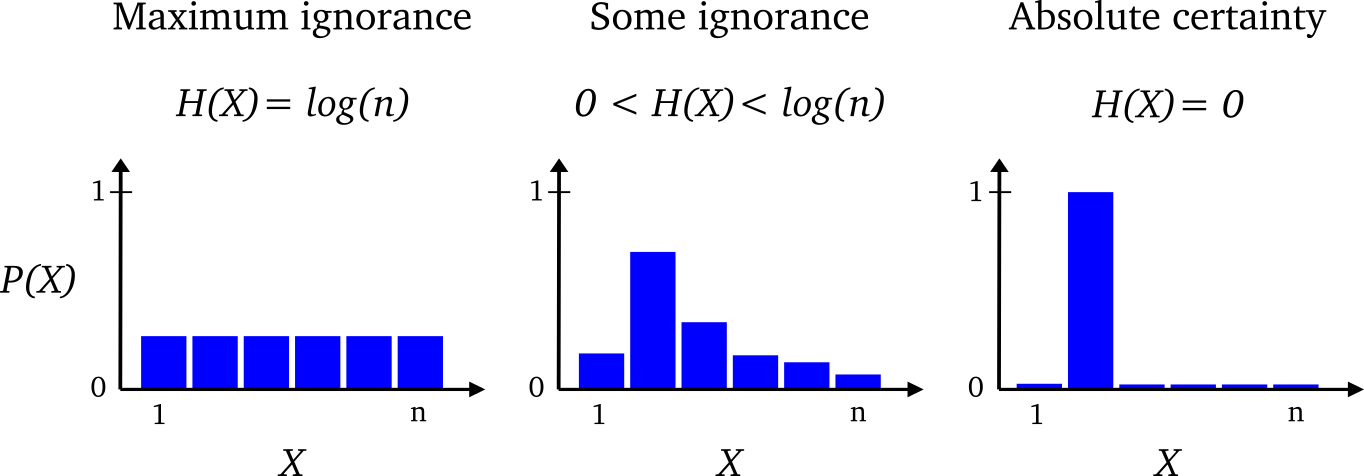
먼저, 가장 오른쪽 그림. 한 값에 확률이 1이고, 나머지에 대해서는 확률이 0인 상황이다. 이 분포를 보면 $X$를 어떤 것이라고 예상할 수 있을까? “$X$는 항상 2다.” 라고 확실하게 말할 수 있을 것이다. 이런 분포는 확실한 분포이고, 그래서 불확실성인 엔트로피 값은 0이다. 두 번째로 가장 왼쪽 그림, 균등 분포이다. 이 분포를 보면 $X$가 어떤 것이라고 예상할 수 있는가? $X$가 무엇이라고 특정지을 수 없을 것이다. 그래서 불확실성이 제일 높다. 불확실성이 높을수록 균등분포에 가깝다.
강화학습에서는 Maximization Entropy 기법이 많이 등장한다. 어떤 매개변수로 표현되는 분포 $p_\theta$를 찾는데, 분포가 큰 엔트로피 값을 갖도록 매개변수 $\theta$를 찾는 기법이다. 불확실성이 큰 것이 나쁜 것만은 아니다. 예를 들어, 정책을 찾을 때, 엔트로피 값이 큰 정책은 어느 한 행동을 확실하게 선택하지 않고, 확률을 골고루 분배해서 exploration을 꾀할 수 있기 때문이다.
Soft policy iteration
본 논문에서는 바로 SAC를 소개하기 전에 policy iteration의 soft 버전인 soft policy iteration을 소개한다. Policy iteration은 주어진 정책의 행동가치함수를 계산하는 policy evaluation과 계산한 행동가치함수를 바탕으로 정책을 개선하는 policy improvement를 반복하며 optimal policy를 찾는 방법이다.
Soft policy evaluation
일반적인 policy evaluation과 다르게, soft policy iteration에서는 주어진 정책 $\pi$의 soft state value를 다음과 같이 정의한다. \[\begin{matrix} V^\pi(s) & = & \mathbb{E}_{a \sim \pi(\cdot | s)}\left[ Q^\pi(s, a) - \log\pi(a|s)\right] & \qquad (1.1) \\ & = & \mathbb{E}_{a \sim \pi(\cdot | s)}\left[ Q^\pi(s, a) \right] + \mathcal{H}((\pi(\cdot | s))) & \qquad (1.2) \end{matrix}\]
식 $(1.1)$이 상태가치함수의 정의이고, 기댓값의 선형성과 엔트로피의 정의를 사용해서 나타낸 것이 식 $(1.2)$이다. 원래 우리가 알고 있는 상태가치함수의 성질에서 확률 분포 $\pi(\cdot | s)$의 엔트로피만 추가된 형태이다. 즉, 상태 $s$에서의 정책 $\pi$의 가치는 행동가치함수의 기댓값에 엔트로피를 보너스로 얹어준 것이다. 엔트로피가 클수록 상태 $s$에서의 가치함수도 커진다는 것을 알 수 있다. 다양한 행동을 많이 할수록 더욱 가치가 높은 상태이다. 가치함수의 정의를 바꿔줬다는 점이 정말 획기적인 것 같다.
Soft policy evaluation은 임의로 초기화된 함수 $Q:\mathcal{S}\times\mathcal{A}\rightarrow\mathbb{R}$에서 시작하여 다음 벨만 오퍼레이터를 반복적으로 적용하여 soft Q-value를 계산한다. \[\mathcal{T}^{\pi}Q(s,a) = r(s,a)+\gamma\mathbb{E}_{s'\sim p(\cdot|s,a)}\left[V(s')\right]. \qquad \qquad (2)\]
이렇게 계속 벨만 오퍼레이터를 적용하면 soft Q-value로 수렴한다는 이론과 증명이 논문에 잘 나와있다. 증명은 policy iteration이 optimal policy로 수렴한다는 이론을 잘 알고 있다면 쉽게 이해할 수 있다. 주어진 정책 $\pi$에 대해서 엔트로피를 딱 계산할 수 있기 때문에 soft state value의 엔트로피텀은 단순 translation에 지나지 않다는 것을 이용한다.
Soft policy improvement
우리가 흔히 알고 있는 Policy iteration의 Policy improvement 단계에서는 각 상태에서 행동가치함수가 가장 높은 행동을 하도록 정책을 수정한다. 즉, \[\pi_k(a|s)=\begin{cases}1 & \text{if }a=\operatorname*{argmax}\limits_{a \in \mathcal{A}}Q^{\pi_{k-1}}(s,a) \\ 0 & \text{otherwise}\end{cases}. \qquad \qquad (3)\]
하지만 SAC에서는 행동가치함수가 높을수록 점점 더 높은 확률을 부여하도록 정책을 수정해나간다. 이를 soft policy improvement라고 부른다. 함수값에 따라 확률을 부여할 수 있는 가장 자연스러운 방법은 지수함수를 사용하는 것이다. Soft policy improvement는 다음과 같이 정책을 개선한다. \[\pi_k(\cdot|s)=\operatorname*{argmin}\limits_{\pi}\operatorname{D}_{\text{KL}}\left(\pi(\cdot|s)\bigg\Vert\frac{\exp\left(Q^{\pi_{k-1}}(s, \cdot)\right)}{Z^{\pi_{k-1}}(s)}\right), \qquad \qquad (4)\]
여기서 $\operatorname{D}_{\text{KL}}$ 은 Kullback-Leibler Divergence, $Z^{\pi}$ 는 확률분포를 만들어주기 위한 정규화텀이다. 이렇게 찾은 $\pi_k$ 의 가치함수는 $\pi_{k-1}$ 의 가치함수보다 항상 크거나 같다는 것이 논문에 잘 증명되어 있다 (monotonic improvement).
Soft policy iteration
Soft policy evaluation과 soft policy improvement를 반복하면 optimal policy로 수렴한다고 한다. 이 역시 증명은 policy iteration의 증명과 같다.
Soft Actor-Critic
이제 Soft Actor-Critic (SAC)에 대해서 소개하고자 한다. Soft policy iteration에 off policy 기반 actor critic를 적용한 것이 SAC라고 생각해도 좋다. 논문에 나와 있는 알고리즘은 다음과 같다.

준비물
SAC에서는 총 5개 funcion approximator (보통 인공신경망)가 필요하다.
- 1개의 policy $\pi_{\phi}$
- 2개의 state value function $V_\psi$, $V_{\bar{\psi}}$
- $\bar{\psi}$ 는 target network로 $\psi$를 사용해서 업데이트된다. (알고리즘의 밑에서 세 번째 줄)
- 2개의 soft Q-function $Q_{\theta_1}$, $Q_{\theta_2}$
- $\theta_1$과 $\theta_{2}$ 는 target 관계가 아니며, TD3처럼 overestimation을 줄이기 위해 2개를 유지하는 것이다.
- $\pi_\phi$ 와 $V_{\psi}$ 를 업데이트 할 때, $\theta_1$과 $\theta_{2}$ 중 더 작은 gradient를 만드는 $\theta$를 사용한다.
State value function 학습
State value function은 식 $(1)$을 이용하여 학습된다. 실제 soft state value에 대해서는 식 $(1)$이 성립하기 때문에 좌변과 우변의 차이 제곱을 최소화하는 것을 목표로 한다. 즉, state value function 학습을 위한 목적함수는 다음과 같다. \[J_V(\psi)=\mathbb{E}_{\mathbf{s}_t \in \mathcal{D}}\left[ \frac{1}{2}\left(V_\psi(\mathbf{s}_t) - \mathbb{E}_{\mathbf{a}_t \ \sim {\pi_\phi}}\left[ Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t) - \log \pi_{\phi}(\mathbf{a}_t|\mathbf{s}_t) \right] \right)^2 \right]. \qquad \qquad (5)\]
실제 그레디언트는 구하기 어렵기 때문에 stochastic gradient descent를 사용하여 그레디언트를 추정한다. \[\hat{\nabla}_\psi J_V(\psi)=\nabla_\psi V_\psi(\mathbf{s}_t)\left( V_\psi(\mathbf{s}_t)-Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t) + \log \pi_{\phi}(\mathbf{a}_t|\mathbf{s}_t) \right). \qquad \qquad (6)\]
기댓값 대신 실제 샘플 $(\mathbf{s}_t, \mathbf{a}_t)$을 대입하고, chain rule을 사용해서 그레디언트를 계산한 것이다.
Soft Q-function 학습
Soft Q-function은 temporal difference learning을 사용하여 업데이트한다. 즉, soft Q-function 학습을 위한 목적함수는 다음과 같다. \[J_Q(\theta)=\mathbb{E}_{(\mathbf{s}_t, \mathbf{a}_t)\sim \mathcal{D}} \left[\frac{1}{2} \left( Q_\theta (\mathbf{s}_t, \mathbf{a}_t) - \hat{Q}_{\theta}(\mathbf{s}_t, \mathbf{a}_t) \right)^2 \right], \qquad \qquad (7)\]
where \[\hat{Q}_{\theta}(\mathbf{s}_t, \mathbf{a}_t) = r(\mathbf{s}_t, \mathbf{a}_t)+\gamma \mathbb{E}_{\mathbf{s}_{t+1}\sim p(\cdot|\mathbf{s}_t, \mathbf{a}_t)} \left[ V_{\bar{\psi}}(\mathbf{s}_{t+1}) \right]. \qquad \qquad (8)\]
샘플을 이용한 stochastic gradient는 다음과 같다. \[\hat{\nabla}_{\theta}J_Q(\theta)=\nabla_{\theta}Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t)\left( Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t)-r(\mathbf{s}_t, \mathbf{a}_t) - \gamma V_{\bar{\psi}}(\mathbf{s}_{t+1})\right). \qquad \qquad (9)\]
Soft value function 안에 $\theta$가 있는데도 chain rule이 적용되지 않은 이유는 타겟 네트워크 $V_{\bar{\psi}}$가 사용되어서 숫자로 취급되기 때문이다.
Policy 학습
이 부분도 굉장히 흥미롭다. 우리가 알고 있는 policy gradient는 평균 상태가치함수 $\mathbb{E}_{\pi}\left[V_\pi(s)\right]$를 최적화하는 것으로부터 유도되었다. 하지만 이 논문에서는 상태가치함수의 정의가 다르기 때문에 다른 방식으로 policy를 학습하게 된다. Soft policy improvement를 목적함수로 사용하여 policy를 학습한다. \[J_{\pi}(\phi)=\mathbb{E}_{\mathbf{s}_t \sim \mathcal{D}}\left[ \operatorname{D}_{\text{KL}}\left( \pi_{\phi}(\cdot|\mathbf{s}_t) \bigg\Vert \frac{\exp (Q_{\theta}(\mathbf{s}_t, \cdot))}{Z_{\theta}(\mathbf{s}_t)}\right) \right]. \qquad \qquad (10)\]
KL divergence의 정의는 다음과 같다. \[\operatorname{D}_{\text{KL}}(p \Vert q)=\mathbb{E}_{X\sim p(x)}\left[\log \frac{p(X)}{q(X)}\right]. \qquad \qquad (11)\]
식 $(11)$의 정의를 사용하면 식 $(10)$은 다음과 같이 정리될 수 있다. \[J_{\pi}(\phi)\approx\mathbb{E}_{\mathbf{s}_t \sim \mathcal{D}}\left[ \mathbb{E}_{\mathbf{a}_t\sim\pi_{\phi}(\cdot|\mathbf{s}_t)} \left[\log \pi_{\phi}(\mathbf{a}_t | \mathbf{s}_t) - Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t) \right]\right], \qquad \qquad (12)\]
여기서 $Z_{\theta}$는 $\phi$와 무관하기 때문에 생략했다. 현재 안쪽 기댓값은 $\mathbf{a}_t \sim \pi_{\phi}(\cdot|\mathbf{s}_t)$에 대해 계산된다.
우리는 식 $(12)$ 기댓값의 실제 그레디언트를 직접 구하는대신 경험 데이터 $(\mathbf{s}_t, \mathbf{a}_t)$를 대입하여 기댓값을 추정하고, 그것의 그레디언트를 계산하고 싶다 (stochatic gradient). 데이터 $(\mathbf{s}_t, \mathbf{a}_t)$를 대입한 값을 기댓값의 추정치 로 사용하는 것은 자연스러운 행위이다. 하지만 기댓값의 추정치의 그레디언트 를 계산하는 것은 $\mathbf{a} \sim \pi_{\phi}(\cdot|\mathbf{s}_t)$ 부분을 커버하지 못한다. $\phi$가 변하면 $\pi_{\phi}$가 변하고, 그로 인해 기댓값 계산의 범위 $\mathbf{a} \sim \pi_{\phi}(\cdot|\mathbf{s}_t)$ 즉각적으로 바뀌기 때문이다. 조금 더 쉽게 설명하자면 $\pi_{\phi}(\cdot|\mathbf{s}_t)$의 순간변화를 고려하여 $\log \pi_{\phi}(\cdot|\mathbf{s}_t)$의 순간변화율을 구해야 하는데, stochastic gradient를 사용하면 $\log \pi_{\phi}(\cdot|\mathbf{s}_t)$의 순간변화만 고려하게 되는 셈이다. 물론, 그 부분을 감수하고도 stochastic gradient를 그레디언트의 추정량으로 사용할 수 있다.
논문에서는 reparameterization trick을 사용해서 분산이 낮은 그레디언트를 추정량이 사용하게 된다. 즉, 행동 $\mathbf{a}_t$를 다른 랜덤변수 $\epsilon_t$를 사용하여 나타내게 만들었다. \[\mathbf{a}_t=f_{\phi}(\epsilon_t; \mathbf{s}_t), \; \text{where} \;\epsilon_t \sim \mathcal{N}(\mathbf{0}, I). \qquad \qquad (13)\]
정책에서 $\pi_{\phi}(\cdot|\mathbf{s}_t)$에서 행동 $\mathbf{a}_t$을 샘플링하는 대신 가우시안 분포에서 $\epsilon_t$를 샘플링하고 이를 $f_{\phi}$에 대입하여 행동을 계산하겠다는 의미이다. 식 $(13)$을 식 $(12)$에 대입하면 다음과 같이 정리된다. \[J_{\pi}(\phi)\approx\mathbb{E}_{\mathbf{s}_t \sim \mathcal{D}}\left[ \mathbb{E}_{\epsilon_t \sim \mathcal{N}} \left[\log \pi_{\phi}(f_{\phi}(\epsilon_t; \mathbf{s}_t) | \mathbf{s}_t) - Q_{\theta}(\mathbf{s}_t, f_{\phi}(\epsilon_t; \mathbf{s}_t)) \right]\right], \qquad \qquad (14)\]
이제 식 $(14)$의 안쪽 기댓값은 $\epsilon_t \sim \mathcal{N}(\mathbb{0}, I)$에 대해 계산되기 때문에 $\phi$ 변화에 따른 $\mathbf{a} \sim \pi_{\phi}(\cdot|\mathbf{s}_t)$ 변화를 고려하지 않아도 된다. 식 $(14)$에 경험 데이터 $\mathbf{s}_t$와 샘플링한 $\epsilon_t$를 대입하여 $\phi$에 대한 그레디언트를 계산하면 다음과 같다. \[\hat{\nabla}_{\phi}J_{\pi_{\phi}}(\phi)=\nabla_{\phi} \log \pi_{\phi}(\mathbf{a}_t | \mathbf{s}_t) + \nabla_{\phi}f_{\phi}(\epsilon_t; \mathbf{s}_t)(\nabla_{\mathbf{a}_{t}}\log \pi_{\phi}(\mathbf{a}_t | \mathbf{s}_t) - \nabla_{\mathbf{a}_t}Q_{\theta}(\mathbf{s}_t, \mathbf{a}_t)), \qquad \qquad (15)\]
여기서 $\mathbf{a}_t$는 샘플링한 $\epsilon_t$을 사용해서 $\mathbf{a}_t = f_{\phi}(\epsilon_t;\mathbf{s}_t)$으로 계산한 것이다. 우리가 알고 있는 체인룰에 의하면 식 $(15)$ 우변의 두 번째 텀만 있어야 할 것 같다. 첫 번째 텀 $\nabla_{\phi} \log \pi_{\phi}(\mathbf{a}_t | \mathbf{s}_t)$는 어디서 등장한 것일까? 바로 total derivative 개념 때문이다.
그럼 total derivative에 대해 간략히 알아보자. 설명을 위해 등장하는 $f$는 잠시 동안만 사용될 지역변수이다. Reparameterization에서 설명한 $f_{\phi}$가 아니다.
어떤 함수 $f$가 변수 $x$와 $y$에 의존적일 때 우리는 $f(x, y)$으로 적어준다. 쉬운 이해를 위해 $f(x, y) = xy + y^2$인 함수 $f$가 있다고 하자. 함수 $f$를 $x$에 대해 편미분할 때 우리는 $y$를 상수 취급한다. 즉, \[\frac{\partial f}{\partial x} = y.\]
그런데 만약 $y$가 $x$에 의존적이면 어떨까? 예를 들어, $y = x^2$인 의존성이 있다면 어떨까? $x$가 변하면 $y$도 변하고, $x$와 $y$의 변화에 의해 $f$가 변한다. 변수와 변수 사이의 의존성까지 고려하여 계산하는 미분을 total derivative라고 한다. 함수 $f$에 대한 $x$의 total derivative는 다음과 같이 계산된다. \[\frac{df}{dx}=\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}\frac{dy}{dx}=y + x + 4 x = y + 5x. \qquad \qquad (*)\]
$x$에 의한 $f$의 변화와 $x$에 대한 $y$의 변화 그리고 그것으로 인한 $f$을 변화를 모두 고려하게 되어 준다.
다시 돌아와서 식 $(14)$을 $\phi$에 대해 미분해 줄 때, 체인룰의 중간 변수 $\mathbf{a}_t=f_{\phi}(\epsilon_t;\mathbf{s}_t)$가 $\phi$에 의존적인 상황이다. 따라서 편미분인 아닌 total derivative를 계산해줘야 한다. 식 $(15)$ 우변의 첫 번째 텀 $\nabla_{\phi} \log \pi_{\phi}(\mathbf{a}_t | \mathbf{s}_t)$이 식 $(*)$의 $\frac{\partial f}{\partial x}$에 해당하는 부분이다. 그리고 식 $(15)$ 우변의 두 번째 텀은 식 $(*)$의 $\frac{\partial f}{\partial y}\frac{dy}{dx}$에 해당하는 부분이며, 우리가 아는 체인룰 느낌이 난다.
지금까지 SAC의 각 네트워크의 손실함수와 그레디언트에 알아보았다. 지금까지의 내용을 사용해서 SAC 알고리즘을 수행하면 된다.
Experiment
SAC 논문에서는 OpenAI gym benchmark suite와 rllab의 Humanoid 환경을 사용하여 실험을 하였다. 논문에서는 다음 다섯 가지 알고리즘을 비교하고 있다.
- DDPG: off-policy, actor-critic
- PPO: on-policy, policy
- Soft Q-learning (SQL): off-policy, Q-learning for learning maximum entropy policies with two Q-networks
- TD3: off-policy, actor-critic, two Q-networks
- SAC: off-policy, actor-critic, two Q-networks for learning maximum entropy policies
결과는 다음과 같다.
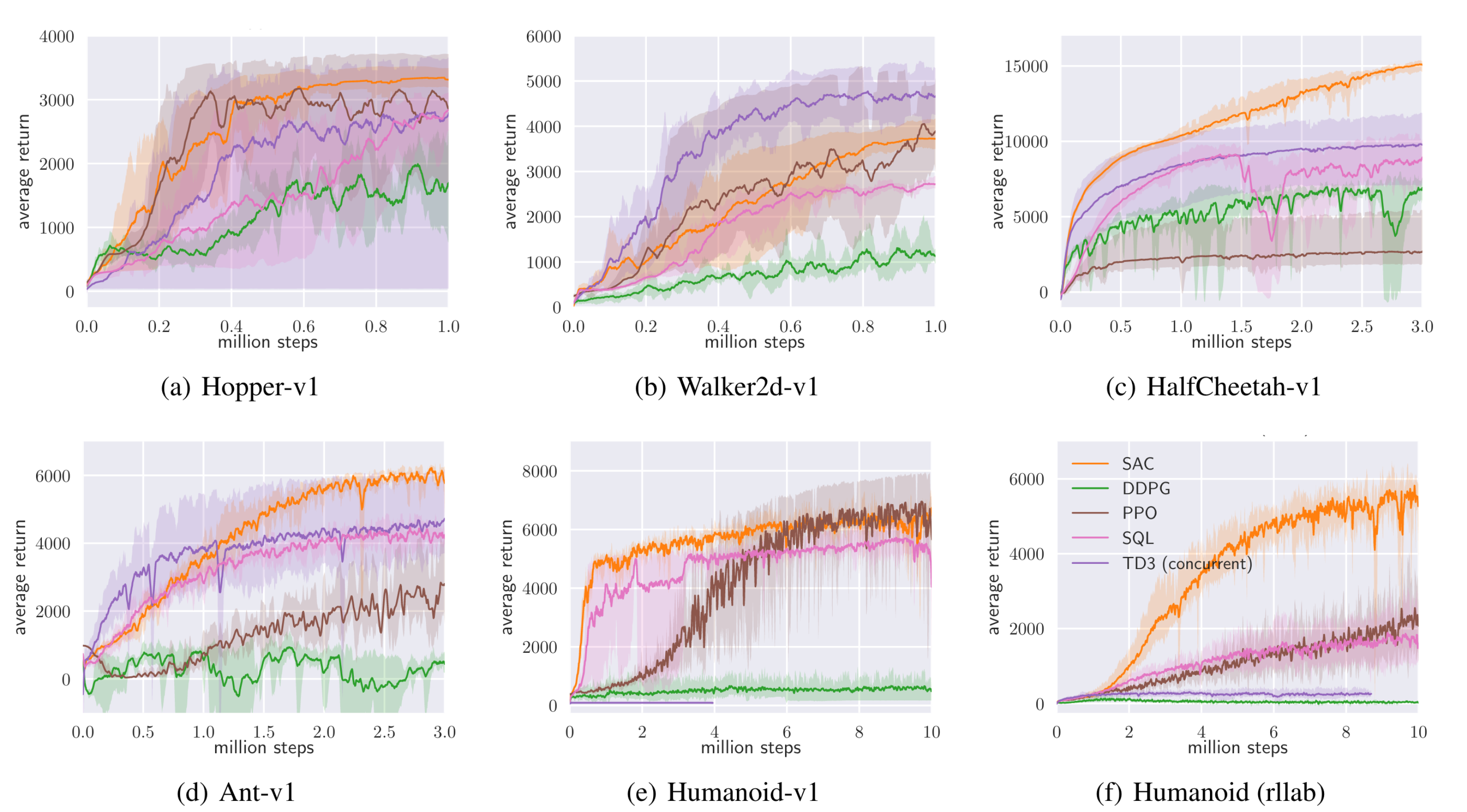
특히, Humanoid 환경의 경우 21차원의 행동공간을 갖는 복잡한 환경이다. 많은 off-policy 알고리즘들은 학습 불안정성 때문에 humanoid 환경을 해결하지 못한다. 하지만 SAC는 soft policy improvement를 통해 stochastic policy를 학습하게 되는데, 이로 인해 안정적인 학습이 가능하여 humanoid 환경을 해결할 수 있었다. Stochatic policy가 학습 안정성을 더한다는 것을 보이기 위하여 SAC의 deterministic policy 변형체를 만들어서 humanoid에 실험을 했는데, 결과는 다음과 같다.
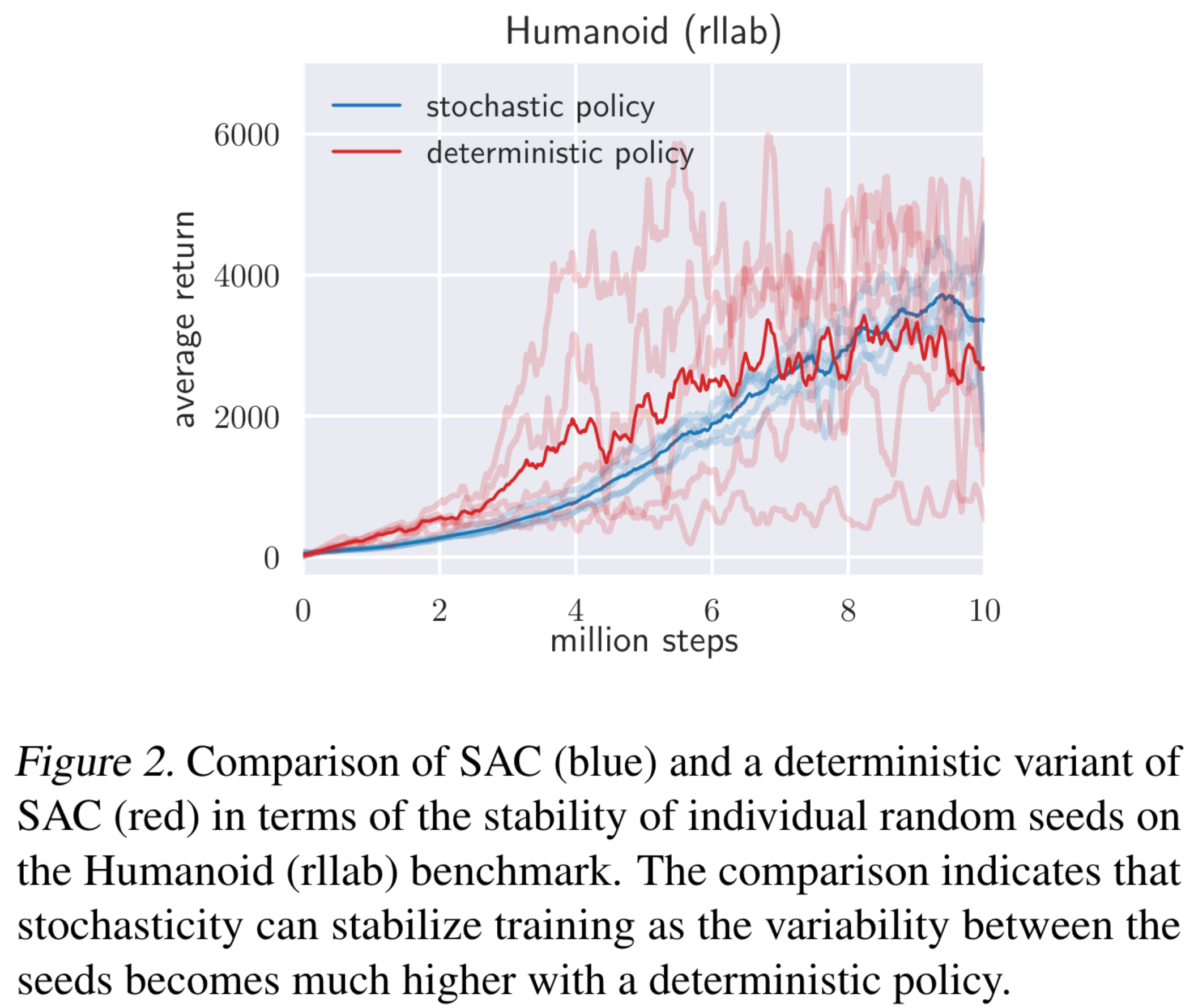
SAC에서 중요한 하이퍼 파라미터는 reward scale이다. 뜬금 없이 보상의 스케일이 중요한 이유는 보상의 스케일에 따라, 식 $(1)$에 있는 엔트로피텀의 영향력이 달라지기 때문이다. 보상의 스케일을 달리하며 Ant-v1에 실험한 결과는 다음 그림의 가운데에 나타나 있다. 참고로 $(a)$는 학습이 종료된 후 evaluation rollout에서 stochastice policy를 사용할지 또는 exploitation을 위해 deterministic policy를 사용할지에 따른 결과이다. $(c)$는 타겟 가치함수 업데이트에 사용되는 $\tau$ 파라미터에 대한 그림이다.
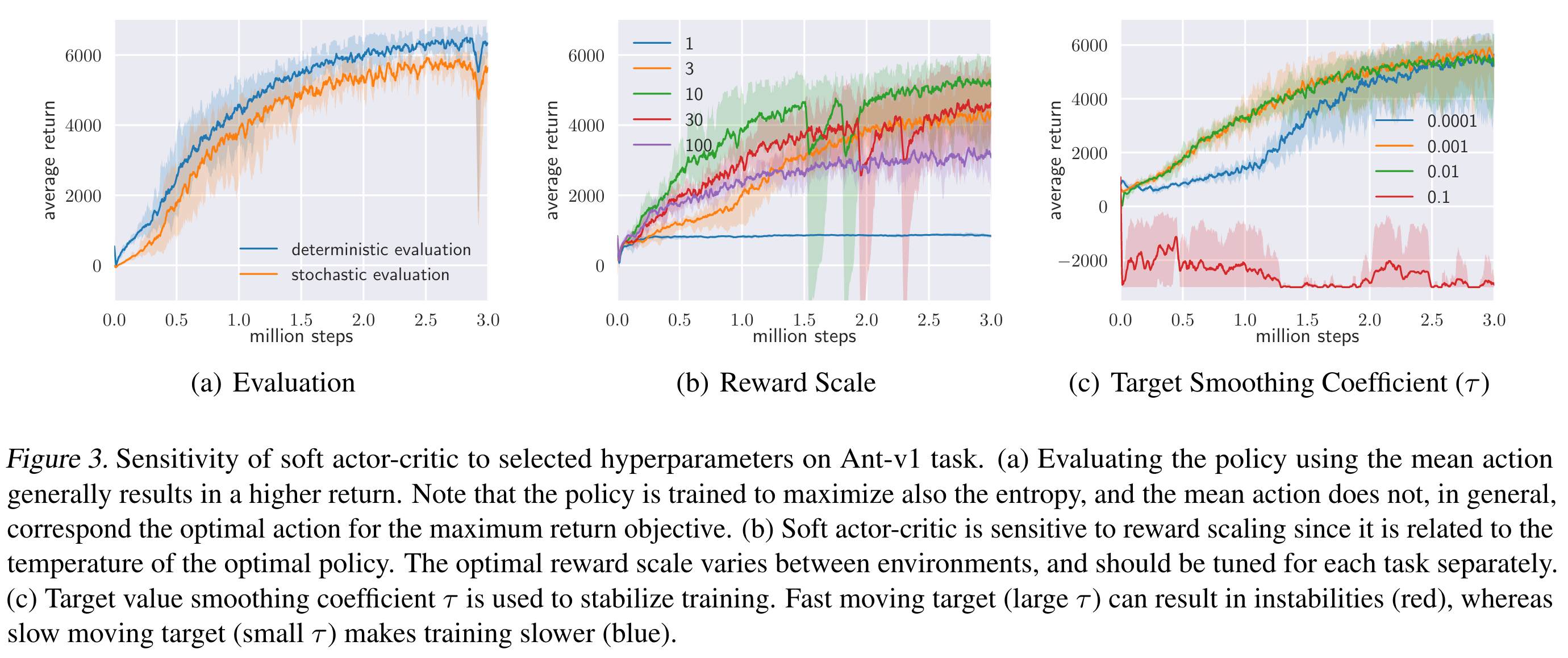
끝맺음말
강화학습 공부 시작한지 얼마 지나지 않아 이 논문을 읽었을 때 너무나도 어려웠는데, 이번에 읽으니 너무 쉽게 잘 이해가 되었다. 나 제법 성장해버린 것일지도…? 한편, 식 $(15)$을 이해하기 너무 어려웠다. 지금은 왜 그런 식이 유도됐는지 약간만 유추 가능한 상태이다. 해당 식을 완전히 유도하기 위해서는 미적분은 물론 확률론까지 알아야 할 것 같다. 이론을 까먹기 전에 코드를 따라 써봐야 할 것 같다.

