Robust Random Cut Forest (RRCF)
오늘의 논문 먹방은 바로 “Robust Random Cut Forest Based Anomaly Detection On Streams” 으로 2016년 ICML에 게재된 논문입니다. 이 논문에서 제안하는 Robust random cut forest (RRCF) 모델은 트리 기반 이상 감지 모델입니다. RRCF는 가장 대표적인 트리 기반 이상 감지 모델인 Isolation Forest와 차이가 거의 없습니다. 하지만 그 작은 차이가 엄청난 기여를 만들어냈습니다.
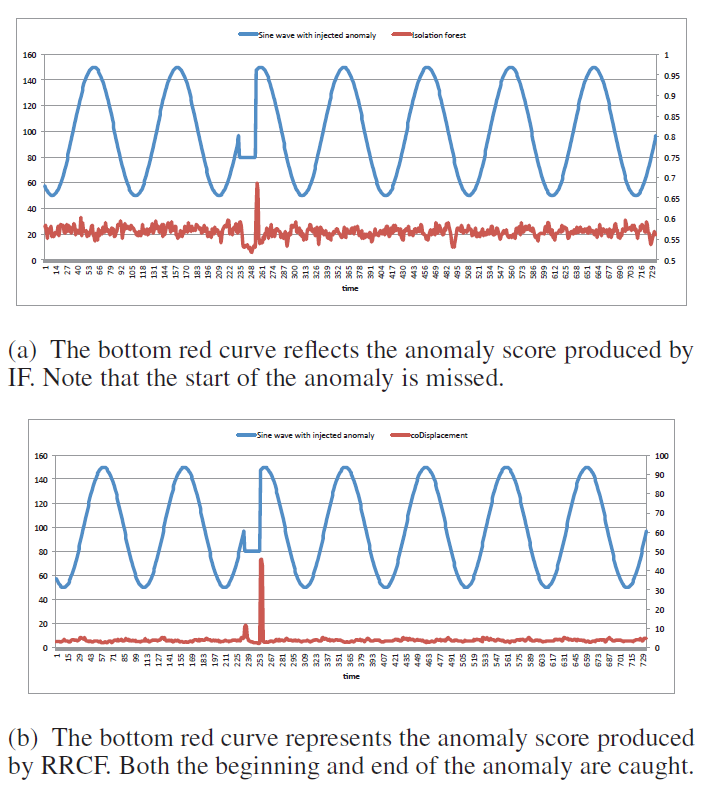
위 그림은 제 마음대로 선정한 이 논문의 메인 figure 입니다. 파란색 선은 사인 그래프에서 235~255 구간을 이상 신호로 변환한 것입니다. 빨간색 선은 데이터의 이상 정도를 나타내는 이상 스코어입니다. 이 값이 높으면 데이터를 이상 데이터로 간주하게 됩니다. IF (위 그래프)의 경우 이상 신호가 모두 끝난 후에야 이상 스코어 값이 높아집니다. 반면에 RRCF (아래 그래프)의 경우 이상 신호의 시작점과 종료점에서 모두 이상 스코어가 높습니다. 실제 세계 문제에서는 대부분 실시간 이상 감지를 요구하는 것을 고려하면 RRCF의 이상 스코어가 더욱 합리적이라고 생각됩니다.
들어가기 전에
- 이 논문이 2016년 논문이라는 것을 유념하고 읽어주시길 바랍니다. 최신 동향과는 맞지 않을 수 있습니다.
Isolation Forest를 알고 있으면 포스팅 이해에 도움이 될 것입니다. 이와 관련하여 고려대학교 강필성 교수님의 강의 영상을 추천드립니다.
이 포스트에서 다룰 내용들
기존 이상감지 모델들의 한계점
2008년 이전까지의 이상 감지 모델들은 밀도 (density) 기반 또는 거리 (distance) 기반이었습니다.
- 밀도 기반 모델들은 데이터들의 확률밀도함수를 모델링하여, 특정 데이터가 등장할 확률이 낮으면 해당 데이터를 이상 데이터로 간주합니다.
- 거리 기반 모델들은 데이터 사이의 거리를 모두 계산하여, 다른 데이터들에 비해 멀리 동 떨어진 데이터를 이상 데이터로 간주하는 방법입니다.
두 방법론들 모두 각각의 장단점이 있겠지만, 데이터의 양과 차원 수가 높을 경우 계산 복잡도도 굉장히 높고 성능은 오히려 떨어지는 단점이 있었습니다. 직관적으로 생각했을 때,
- 데이터의 양이 증가할수록 이상 데이터도 증가할 것입니다. 만약 이상 데이터가 모여 작은 군집을 이룬다면 위 두 방법론들이 잘 적용되지 않을 것입니다.
- 데이터의 차원이 증가할수록 확률밀도함수를 추정하기 어려울 것입니다.
Isolation Forest
2008년 기존의 방법론들과는 전혀 다른 방식인 트리 기반의 이상 감지 모델 Isolation Forest (IF)가 등장하게 됩니다. 오늘 소개하고자 하는 RRCF는 IF의 변형체이기 때문에 IF의 아이디어를 아주 간단하게 짚고 넘어가도록 하겠습니다. 보다 더 자세한 내용은 참고문헌 [2]를 참고해주시면 좋을 것 같습니다.
IF는 iTree라고 불리는 트리를 다음과 같이 만듭니다.
- 임의의 feature $p$와 임의의 값 $q$를 선택합니다.
- 다음으로, feature $p$의 값이 $q$보다 작은 데이터와 큰 데이터를 각각 왼쪽 자식 노드와 오른쪽 자식 노드로 분기시킵니다.
- 트리의 모든 leaf 노트가 (이론상) 하나의 데이터만 가질 때까지 위 과정을 수행합니다.
이런 트리를 만드는 이유는
- 이상 데이터의 경우 정상 데이터로부터 멀리 떨어져 있기 때문에 상대적으로 적은 분기만으로 고립시킬 수 있을겁니다. 따라서 이상 데이터는
iTree에서 루트 노드와 가까운 곳에 위치할 것입니다. - 정상 데이터는 서로 뭉쳐 있기 때문에 각각을 고립시키기 위해서는 더 많은 분기를 필요로 할 것입니다. 따라서 정상 데이터는
iTree에서 루트 노드와 먼 곳에 위치할 것입니다.
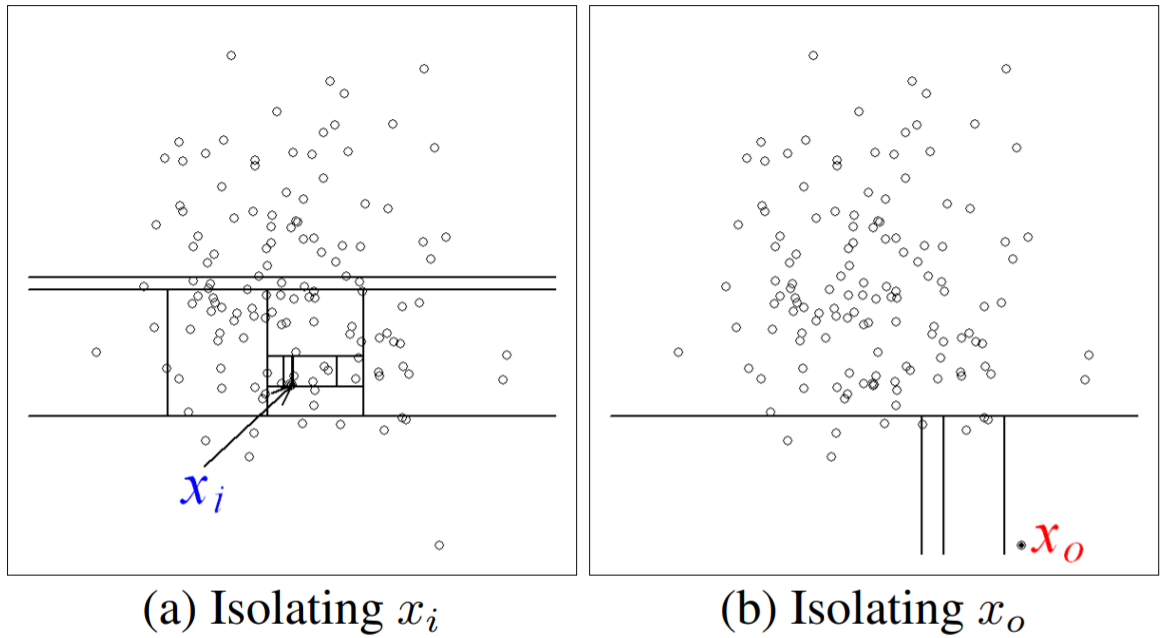
위의 왼쪽 그림을 보면 정상 데이터 $x_i$를 나누기 위해서는 12번의 분기 (수직,수평선의 개수)가 필요했습니다. 반면, 오른쪽 그림을 보면 이상 데이터 $x_o$를 나누기 위해서 단 4번의 분기가 필요했습니다. 따라서 IF에서는 iTree를 여러 개 만들고 각 데이터가 고립되기까지의 평균 분기 횟수 (average path length)를 사용하여 이상 스코어를 정의합니다. 이상 스코어가 설정한 기준보다 높으면 이상 데이터로 간주하고 기준보다 낮으면 정상 데이터로 간주합니다.
글만 읽었을 땐 이 알고리즘이 잘 작동할까 의문이 들 수 있습니다. 몇가지 의문점들을 해소하고 가도록 하겠습니다.
- 데이터가 많으면 모든 데이터를 고립시키기 위해 엄청난 연산이 필요하지 않은가?
IF에서는 모든 데이터를 사용하여iTree를 만들지 않습니다. 하나의iTree는 임의로 서브샘플링된 데이터, 예를 들어 256개,로 만들어집니다.IF는 여러 개의 트리를 만들기 때문에 모든 데이터를 충분히 여러 번 사용할 수 있을 것입니다.- 각각의 트리가 무한하게 분기하는 것을 막기 위하여 트리의 최대 깊이를 설정합니다. 트리의 최대 깊이에 도달할 정도의 데이터라면 정상 데이터일 확률이 높을 것입니다.
iTree는 이진 탐색 트리 (BST) 구조를 갖기 때문에 계산 복잡도가 굉장히 낮습니다. Parameter estimation 또는 pairwise distance를 필요로 하는 알고리즘에 비해 굉장히 빠릅니다.
- 이상 데이터가 서로 뭉쳐 있으면 이상 데이터 역시 필요한 분기 횟수가 많지 않은가?
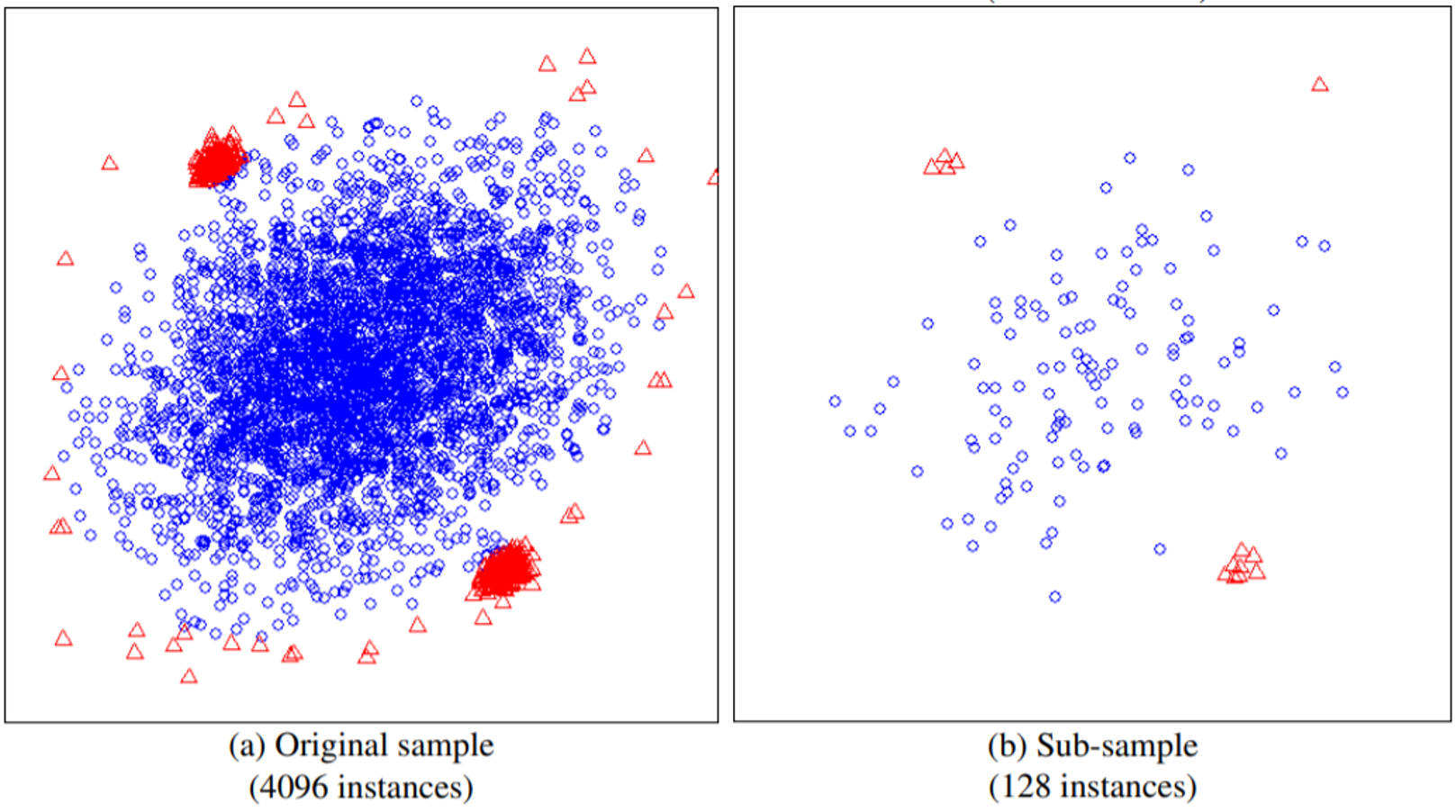
- 이 문제 역시 서브샘플링에 의해 완화될 수 있습니다. 전체 데이터에서 이상 데이터가 뭉쳐 있더라도, 서브샘플링을 통해 밀도가 희소해질 수 있습니다. 아래 그림을 보시면 전체 데이터 공간에서는 뭉쳐있던 이상 데이터 (빨간 세모)들이 서브 샘플링 공간에서는 희소하게 분포하는 것을 볼 수 있습니다.
- 이상 데이터일 수록 평균 분기 횟수가 작다고 했는데, 왜 이를 사용한 이상 스코어는 높을 수록 이상 스코어로 간주하는가?
- 이상 스코어는 $2^{-\frac{\text{평균 분기 횟수}}{\text{어떤 상수}}}$로 이해하시면 좋을 것 같습니다. 따라서 평균 분기 횟수가 적으면 이상 스코어가 증가합니다.
- 훈련 과정과 테스트 과정이 잘 구분되지 않는다.
- 훈련 데이터로부터 여러 개의
iTree를 만드는 것이 훈련 과정입니다. 그리고 모든 과정이 레이블을 필요로 하지 않는 비지도학습입니다. - 새로운 데이터가 유입되면 훈련 과정에서 만든
iTree들을 통과시켜 평균 분기 횟수를 셈하여 이상 스코어를 계산하게 됩니다.
- 훈련 데이터로부터 여러 개의
Robust Random Cut Forest
위에서 언급한 한계점들을 해결하기 위해 본 논문에서는 Robust random cut forest (RRCF)를 제안합니다. RRCF는 IF와 크게 두 부분만 다릅니다.
- Feature $p$를 선택할 때 uniform random하게 뽑는 대신, 각 feature가 갖는 값의 범위에 따라 확률을 다르게 부여하여 선택합니다.
- 평균 분기 횟수 대신,
Collusive displacement (CoDisp)라는 새로운 이상 스코어를 사용합니다.
1번 변경사항은 실시간 스트리밍 환경에서도 이상 감지 모델이 잘 동작할 수 있게 만들어줍니다. 2번 변경사항은 이상 데이터를 다른 관점으로 정의함으로서 이상 감지 성능을 향상시켰습니다.
이번 섹션은 다음과 같이 구성되어 있습니다.
- Robust radnom cut tree (RRCT)
- 실시간 스트리밍 환경
- Displacement
- Collusive Displacement
- 최종적인 알고리즘
Robust random cut tree (RRCT)
RRCF의 각 트리는 다음과 같이 만들어집니다. 주어진 (서브샘플링 된) 데이터셋 $S$에 대하여 robust random cut tree (RRCT) $\mathcal{T}(S)$는 다음과 같이 만들어집니다. (RRCT 생성 알고리즘)
- 랜덤하게 feature $p$를 선택합니다. 이때, $i$번 째 feature가 선택될 확률은 $\frac{l_i}{\sum_j l_j}$ 입니다. 여기서 $l_i=\max_{x \in S}x_i-\min_{x \in S} x_i$ 입니다.
- $[\min_{x \in S} x_i, \max_{x \in S}x_i]$ 범위에서 uniform random하게 값 $q$를 선택합니다.
- Left child를 $S_1=\{x \mid x \in S, x_i \le q\}$ 로, right child로 $S_2=\{x \mid x \in S, x_i > q\}$로 분기합니다.
- 위를 반복합니다.
이렇게 만든 트리들을 모아놓은 것을 RRCF라고 부릅니다.
IF와 비교하였을 때 다른 점은 feature $p$를 균등하게 선택하는 것이 아닌 각 feature가 갖는 값의 범위에 따라 서로 다른 확률을 부여하여 선택한다는 것입니다. 이 작은 차이만으로 시간에 따라 분포가 점점 달라지는 데이터에 대응하여 트리를 만들 수 있게 됩니다. 따라서 논문에서는 RRCF가 실시간 스트리밍 데이터에 적합한 알고리즘이라고 주장하고 있습니다. 잠시 이 주제를 짚고 넘어가도록 하겠습니다.
실시간 스트리밍 환경
실시간 스트리밍 환경에서는 시간의 흐름에 따라 유입되는 데이터의 분포가 달라질 수 있습니다. 과거 데이터를 학습한 모델이 앞으로 유입되는 데이터에 대해서도 좋은 성능을 보일 것이라는 보장은 없습니다. 따라서 새롭게 유입되는 데이터들을 계속 모델 학습에 사용해야 합니다. 예를 들어, 현재 시점이 $t$일 때, 가장 최근 256개의 데이터로 트리를 구성한다고 생각해보겠습니다.
- $S_t=\{\mathbf{x}_{t-255}, \mathbf{x}_{t-254},\cdots, \mathbf{x}_t\}$
- $\mathcal{T}(S_t)$ : $S_t$로 만든
RRCT
다음 시점으로 넘어가면 $S_{t+1}=\{\mathbf{x}_{t-254},\cdots,\mathbf{x}_{t},\mathbf{x}_{t+1}\}$ 을 이용하여 RRCT를 다시 만들어야 합니다. 이때, RRCT 생성 알고리즘을 통해 $\mathcal{T}(S_{t+1})$ 을 만들 수도 있겠지만, 이미 만들어놓은 $\mathcal{T}(S_t)$를 사용해서 만들 수 있다면 더욱 효율적일 것입니다. RRCT는 결국 각 leaf 노드가 (이론상) 데이터 한 개인 트리이기 때문에 $\mathcal{T}(S_t)$에서 $\mathbf{x}_{t-255}$를 삭제하고, $\mathbf{x}_{t+1}$ 추가하여 $\mathcal{T}’(S_{t+1})$을 만들 수 있습니다.
이때, $\mathcal{T}(S_{t+1})$은 RRCT 생성 알고리즘으로 만든 것이고, $\mathcal{T}’(S_{t+1})$은 $\mathcal{T}(S_t)$을 변형해서 만든 것을 유념하셔야 합니다.
RRCT 생성 알고리즘는 feature $p$와 값 $q$의 선택에 따라 무수히 많은 $\mathcal{T}(S_{t+1})$을 만들 수 있습니다.- 즉, $\mathcal{T}(S_{t+1})$을 random variable으로 간주하고 확률분포를 생각해볼 수 있습니다.
- $\mathcal{T}’(S_{t+1})$은 $\mathcal{T}(S_t)$에서 $\mathbf{x}_{t-255}$를 삭제하고, $\mathbf{x}_{t+1}$ 추가하여 유일하게 결정됩니다. 즉, $\mathcal{T}’(S_{t+1})$은 $\mathcal{T}(S_t)$에 종속적입니다.
- 마찬가지로, $\mathcal{T}(S_t)$을 random variable으로 간주하고 $\mathcal{T}’(S_{t+1})$의 확률분포를 생각해볼 수 있습니다.
- 마찬가지로, $\mathcal{T}(S_t)$을 random variable으로 간주하고 $\mathcal{T}’(S_{t+1})$의 확률분포를 생각해볼 수 있습니다.
여기서 주목해야할 것은 $\mathcal{T}(S_{t+1})$의 확률분포와 $\mathcal{T}’(S_{t+1})$의 확률분포가 같을 것이라고 기대하기는 힘듭니다. 단순히 생각해봐도
- $\mathcal{T}(S_{t+1})$은 $S_{t+1}$의 feature 값들의 최소/최대값을 사용하여 만들어지고,
- $\mathcal{T}’(S_{t+1})$은 $S_{t}$의 feature 값들의 최소/최대값을 사용하여 만들어진 트리에 노드 삭제/추가 연산만 더해진 것
뿐이기 때문입니다. 그리고 두 확률분포가 다르다는 이야기는 다음과 같습니다.
- 실시간 스트리밍 환경에서 새로 유입된 데이터를 학습한 모델 $\mathcal{T}(S_{t+1})$의 분포와 다른 분포를 갖는 모델 $\mathcal{T}’(S_{t+1})$을 사용한다는 것입니다.
- 따라서 엉뚱한 트리들로 데이터들의 이상 스코어를 계산할 확률이 증가한다는 것입니다.
하지만 놀랍게도 RRCT 생성 알고리즘으로 생성된 트리에 논문에서 제안하는 노드 추가/제거 알고리즘을 사용하면 $\mathcal{T}(S_{t+1})$와 $\mathcal{T}’(S_{t+1})$의 분포가 같아진다고 합니다. 보다 더 정확한 이론의 statement와 증명은 논문을 참고하시면 좋을 것 같습니다. 왜냐하면 너무 어려워서 저는 읽기를 포기했기 때문입니다.
Displacement (Disp)
IF 섹션에서 언급하지는 않았지만 IF는 “이상 데이터는 수가 적으며, 정상 데이터와는 다른 feature 값을 갖는다”라는 특징에 주목했습니다. 그래서 이상 스코어로 평균 분기 횟수를 사용했습니다. 한편, RRCF는 이상 데이터의 다른 특징에 주목합니다. 바로 이상 데이터의 존재는 모델의 복잡성을 증가시킨다는 점입니다. 논문에서는 이에 대한 근거를 수학적으로 제시하지 않았기 때문에 이 포스팅에서는 직관적인 설명만 더하려고 합니다.
정상 데이터만 있을 때는 학습 모델이 정상 데이터의 분포만 학습하면 됩니다. 한편, 이상 데이터는 정상 데이터와 다른 값의 분포를 갖습니다. 따라서 이상 데이터가 있을 때 학습 모델은 정상 데이터의 분포 뿐만 아니라 이상 데이터의 분포도 학습해야 합니다. 따라서 모델의 복잡성이 증가하게 됩니다. RRCT 모델로 다음 예시를 살펴보겠습니다. 이상 데이터의 존재가 어떻게 분기 횟수를 증가시키는지에 주목하시면 좋을 것 같습니다.
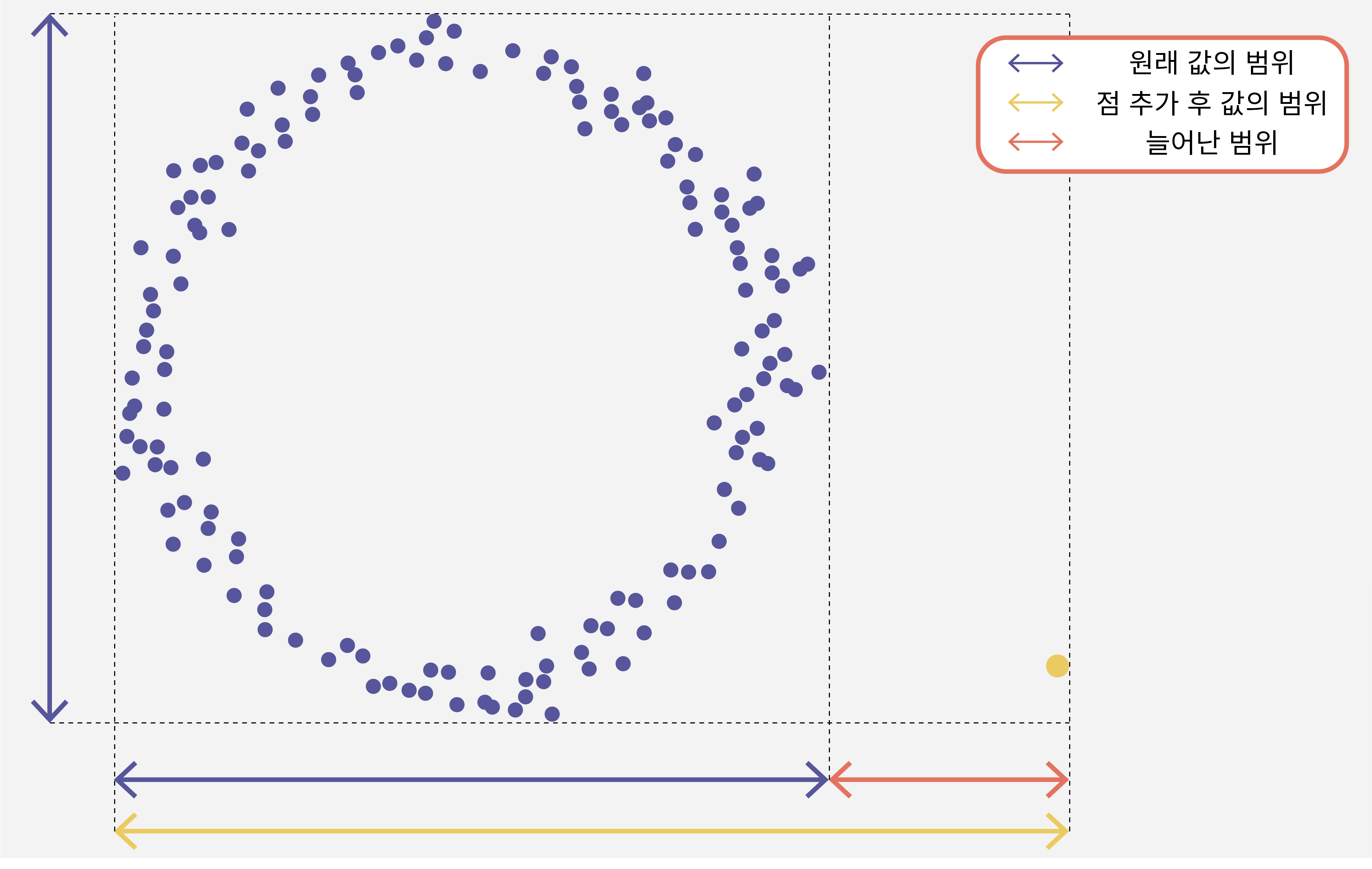
위 그림을 보겠습니다. 원형으로 분포한 데이터들로 만든 RRCT와 거기에 노란색 점이 추가된 RRCT를 비교해볼 것입니다.
- 노란색 점이 추가될 경우, 노란색 점을 고립시키기 위하여, 늘어난 범위 (빨간 범위) 안에서 적어도 한번의 분기가 더 필요할 것입니다.
- 예를 들어, 첫 분기에서 운 좋게 노란색 점을 고립시키면, 나머지 과정은 원래 데이터로
RRCT를 만드는 과정과 같을 것입니다.- 이 경우 원래 데이터로 만든
RRCT에서 최상단에 분기 하나를 더 추가한 트리가 만들어질 것입니다. - 따라서, 이상 데이터가 추가된
RRCT에서는 원형으로 분포한 모든 데이터들의 path length가 1만큼 증가하게 됩니다.
- 이 경우 원래 데이터로 만든
- 첫 분기에서 노란색 점이 고립되지 않았더라도 언젠가는 노란색 점이 고립되어야만 합니다. 예를 들어, $d$ 번 째 분기에서 노란색 점이 고립되었다면,
- $d-1$ 번 째까지 노란색 점과 함께 분기되어 왔던 데이터들은 $d$번 째 분기에 분리되면서, 기존의
RRCT와 비교하면 path length가 1만큼 증가하게 됩니다.
- $d-1$ 번 째까지 노란색 점과 함께 분기되어 왔던 데이터들은 $d$번 째 분기에 분리되면서, 기존의
주목해야할 점은 노란색 점이 추가될 경우, 어떤 데이터들은 기존 RRCT와 비교했을 때 path length가 증가한다는 것입니다. 그리고 path length가 증가하는 데이터들의 개수가 꽤 많을 것이라고 생각해볼 수 있습니다. 그림은 그리지 않았지만, 노란색 점이 정상 데이터 근처에 추가되었다면, path length가 증가하는 데이터가 그리 많지 않을 것입니다.
따라서 이 논문에서는 Disp (displacement)라는 것을 이상 스코어로 사용합니다. 어떤 (서브샘플링 된) 데이터셋 $S$ 안에 있는 한 데이터 $x$의 이상 스코어 $Disp(x, S)$는 다음과 같이 정의됩니다.
- 데이터셋 $S$로 만든
RRCT에서 데이터 $x$를 제거했을 때, 남은 데이터에서 발생하는 depth 변화의 총합입니다. - 사실, 데이터셋 $S$로 만들 수 있는
RRCT는 다양할 수 있기 때문에, 각RRCT에서 $x$를 제거했을 때 발생하는 depth 변화의 총합에 기대값을 취한 것이 $Disp(x, S)$입니다.
이 값은 생각보다 쉽게 구할 수 있습니다. 먼저, 하나의 RRCT에서 데이터 $x$를 제거할 때 생기는 depth 변화의 총합은 데이터 $x$의 자매 노드에 있는 데이터의 개수입니다 (아래 그림 및 설명 참조). 따라서, $Disp(x, S)$는 데이터셋 $S$로 만든 여러 RRCT에서 $x$의 자매 노드에 있는 데이터 개수들의 평균값이 됩니다.
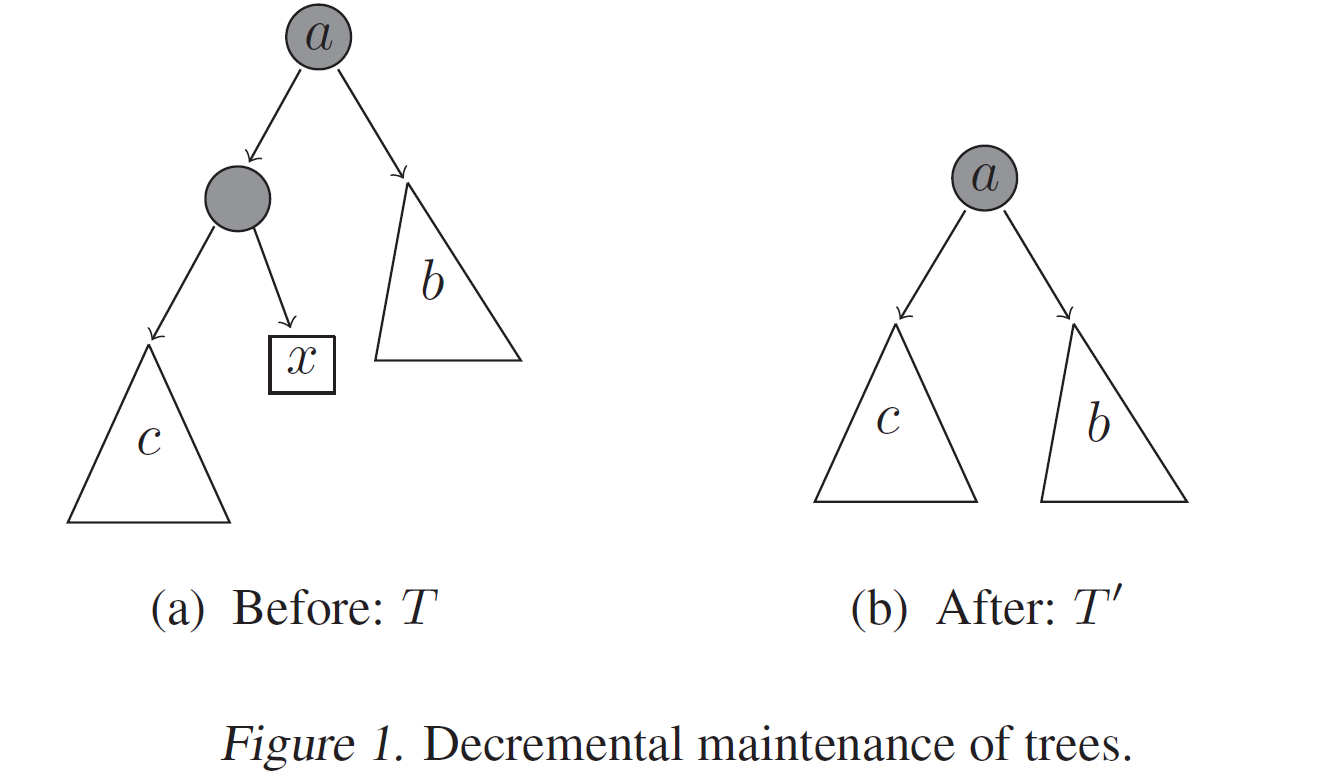
NIMS 산업수학혁신센터의 김민중 박사님의 세미나 [4]에서 Disp에 대한 재밌는 비유가 하나 있었습니다. 회사에서 내가 퇴직하는 상황을 생각해보겠습니다. 내가 만약 굉장히 영향력 있는 팀원이었다면 나의 퇴직은 팀에 굉장히 큰 영향을 미치게 됩니다. 반면, 내가 평범한 수준의 팀원이었다면, 내가 퇴직해도 팀은 큰 영향을 받지 않을 것입니다.
Collusive Displacement (CoDisp)
사실, Disp를 바로 이상 스코어로 사용하기에는 masking 문제에 취약하다는 단점이 있습니다. Masking은 이상 데이터끼리 서로 뭉쳐서 스스로의 정체를 감추는 현상입니다. 이상 데이터 $x$ 바로 옆에 $x’$이 하나 더 있다면, $x$의 자매 노드에 $x’$ 하나만 존재할 것입니다. 따라서 Disp 값은 약 1 정도 밖에 되지 않을 것입니다. 따라서 이 논문에서는 $x$의 정체를 숨기려고 하는 공모자 (colluder)들까지 고려하는 이상 스코어 Collusive Displacement (CoDisp)를 제안합니다.
이상 데이터 $x$의 공모자들의 집합을 $C$라고 하겠습니다. 우리는 데이터셋 $S$로 만든 RRCT 에서 $x$만 제거하는 것이 아니라, $C$를 제거했을 때 발생하는 depth 변화의 총합을 이상 스코어로 사용하고 싶습니다. 즉, $x$에 대한 이상 스코어로 $Disp(x, S)$가 아닌 $Disp(C, S)/\mid C \mid$를 사용할 것입니다. 여기서 집합 $C$의 크기가 클 수록 RRCT에서 $C$를 제거했을 때 트리의 변화가 클 것입니다. 따라서 이상 스코어의 값이 공모자의 수에 영향을 받지 않도록 그 크기로 나눠준 것입니다.
여기서 큰 문제가 하나 있습니다. 우리는 공모자 집합 $C$를 알 수 없습니다. 그냥 있다고 생각하고 논리를 펼쳐왔던 것입니다. 따라서 이 논문에서는 $x$를 포함하는 가능한 모든 부분집합을 고려합니다. 그리고 $Disp(C, S)/\mid C \mid$ 의 최대값을 이상 스코어로 사용합니다. 즉,
$CoDisp(x, S)=\mathbb{E}_{T}[\max\limits_{x \in C \subset S}\frac{Disp(C, S)}{\mid C \mid}]$
$T$는 $S$로 만든 RRCT입니다. 여러 RRCT에 대하여 위의 값을 계산하여 평균을 내서 $CoDisp(x, S)$를 계산하게 됩니다. 물론, 가능한 모든 부분집합 $C$를 고려한다는 것은 불가능합니다. 따라서 실제 구현에서는 RRCT 안에서 $x$의 조상들만 $C$로 간주하여 연산을 진행합니다. 이런 식으로 구현하면 Displacement에서 했던 것처럼 $C$를 제거하였을 때 모델의 depth 변화의 총합을 “$(C\text{의 자매 노드에 있는 데이터의 개수})$”로 쉽게 구할 수 있습니다.
따라서 하나의 RRCT에서 데이터 $x$의 CoDisp 값은 다음과 같이 구할 수 있습니다.
- $x$의 자매 노드에 있는 데이터 개수 / 1
- $x$의 부모 노드의 자매 노드에 있는 데이터 개수 / 부모 노드의 크기
- $x$의 조부모 노드의 자매 노드에 있는 데이터 개수 / 조부모 노드의 크기
- $x$의 증조부모 노드의 자매 노드에 있는 데이터 개수 / 증조부모 노드의 크기
- $x$의 고조부모 노드의 자매 노드에 있는 데이터 개수 / 고조부모 노드의 크기
- $\vdots$
중에서 최대값을 구하면 됩니다. 그리고 이 최대값을 여러 RRCT로부터 계산하고 평균을 내리면 그 값이 $CoDisp$ 값이 되는 것입니다. 참고로 CoDisp 값이 클 수록 이상 데이터로 간주합니다.
최종적인 알고리즘
최종적인 알고리즘을 정리해보겠습니다. 정말 볼품 없어 보이는 수도코드이지만, 논문보다 훨씬 직관적으로 나타냈다고 생각합니다.
Input
- $Z$: 주어진 데이터셋
num_trees: 만들RRCT개수tree_size: 서브샘플링 크기
1. Forest 만들기 (훈련)
forest = []
for i in range(num_trees):
S = Z에서 tree_size개의 데이터 랜덤 샘플링
forest.append(RRCT(S))
2. 새로운 데이터 $x$의 CoDisp 값 구하기
codisp = []
for RRCT in forest:
RRCT.insert_point(x)
disp = []
for C in x의 조상:
disp.append(C의 자매노드 크기 / C의 크기)
codisp.append(max(disp))
RRCT.delete_point(x)
codisp = mean(codisp)
이 짧은 수도코드를 설명하기 위하여 위에서부터 지금까지 일장연설을 해온 것입니다.
실험
이 논문에는 인위 데이터에 대한 실험 두 가지와 실제 데이터에 대한 실험 한 가지가 있습니다. 인위 데이터에 대한 실험은 IF가 이상 데이터를 적절하게 잡아내지 못하는 상황을 제시하며 진행됩니다.
인위 데이터 1. 의미 없는 축이 굉장히 많은 경우
다음과 같은 30차원 데이터 2,010개를 훈련 데이터로 고려해보겠습니다.
- 1,000개의 데이터는 첫 번째 원소만 +5이고, 나머지 29개의 원소는 0인 벡터에 가우시안 노이즈가 추가된 벡터입니다. 즉, $\mathbf{x}_i=(5, 0, 0, \cdots, 0)^T + \mathbf{\epsilon}_i$ where $\mathbf{\epsilon}_i \sim \mathcal{N}(\mathbf{0}_{30}, \mathbf{I}_{30})$ for $i=1, \cdots, 1000$
- 1,000개의 데이터는 첫 번째 원소만 -5이고, 나머지 29개 원소는 0인 벡터에 가우시안 노이즈가 추가된 벡터입니다. 즉, $\mathbf{x}_i=(-5, 0, 0, \cdots, 0)^T + \mathbf{\epsilon}_i$ where $\mathbf{\epsilon}_i \sim \mathcal{N}(\mathbf{0}_{30}, \mathbf{I}_{30})$ for $i=1001, \cdots, 2000$
- 나머지 10개의 데이터는 가우시안 노이즈 벡터로서 이상 데이터를 나타냅니다. 즉, $\mathbf{x}_i= \mathbf{\epsilon}_i$ where $\mathbf{\epsilon}_i \sim \mathcal{N}(\mathbf{0}_{30}, \mathbf{I}_{30})$ for $i=2001, \cdots, 2010$
어떤 양상인지 대충 상상이 되실거라고 믿습니다. 뒤 29개의 축은 노이즈로 이루어져 있기 때문에 이 노이즈 안에서 정상 데이터와 이상 데이터를 구분하기는 어렵습니다. 따라서 트리 모델이 이상 데이터를 고립시키기 위해서는 반드시 첫 번째 축을 선택해야 합니다. 이때, IF는 모든 축을 동일한 확률로 선택합니다. 따라서 $\frac{29}{30}$의 확률로 의미 없는 축을 선택하여 트리를 성장시켜나갈 것입니다. 이로 인해 정상 데이터든 이상 데이터든 상관 없이 평균 path length가 증가하게 되면서 이상 스코어는 감소하게 됩니다. 따라서 IF는 의미 없는 축이 많은 경우에 이상 데이터를 적절하게 잡아낼 수 없습니다. 한편, RRCF의 경우 각 축이 갖는 범위에 따라 축을 선택할 확률이 달라집니다. 따라서 RRCF는 높은 확률로 첫 번째 축을 계속 뽑으면서 이상 데이터를 고립시킬 수 있을 것입니다.
그리고 동일한 세팅에서 이상 데이터 없이 2,000개의 데이터만 사용하여 Forest를 만든 상황을 고려해보겠습니다. 그 후 영벡터 $\mathbf{0} \in \mathbb{R}^{30}$가 테스트 데이터로 들어온 상황을 상상해보겠습니다. IF는 이 점을 이상 데이터로 구분할 수 있을까요? 주의해야 할 점은 훈련 데이터에는 없었던 새로운 데이터가 들어왔다는 점입니다.
IF는 새로 유입된 데이터가 각 트리에서 어디에 위치할지 루트 노드부터 분기를 따라가며 추적합니다. 한편, 트리 안에서 첫 번째 군집과 두 번째 군집이 나뉘는 순간이 있을 것입니다. 그 순간 이후부터는 분기가 $+5$ 주변에서만 일어나거나 또는 $-5$ 주변에서만 일어나게 됩니다. IF는 훈련 데이터의 값의 범위만 사용하여 트리를 만들기 때문입니다. 조금 더 풀어서 설명을 하자면, 영벡터를 $+5$ 또는 $-5$ 군집으로부터 고립시키기 위해서는 사실 $\pm3$ 정도를 기준으로 잡아 분기를 하면 될 것 같습니다. 하지만 훈련 당시 iTree에는 영벡터가 없었기 때문에 두 군집이 나뉘고나서부터는 한 노드에서는 $+5$ 주변에서, 다른 노드에서는 $-5$ 주변에서만 분기 기준을 선택하여 트리를 만들게 됩니다. 결과적으로 영벡터는 미리 만들어놨던 iTree에서 잘 고립되지 않기 때문에 이상 스코어가 굉장히 작게 됩니다.
한편 RRCF의 경우 새로 유입된 데이터를 미리 만들어놨던 RRCT에 추가하는 합리적인 알고리즘이 있습니다. 이 포스팅에서는 노드 삽입/제거 알고리즘을 설명하지는 않았지만, 이상 데이터를 RRCT에 추가할 때,
- 해당 데이터를 고려한 값의 범위에서 분기 기준을 다시 설정해보고.
- 기존 데이터로부터 고립이 되는지 확인하는 과정이 있습니다.
- 이 과정을 통해 유입된 데이터가 고립되는 분기를 찾아서 새롭게 노드로 추가하게 됩니다.
따라서 훈련 과정에서 보지 않은 데이터에 대해서도 트리를 새롭게 만들어서 이상 스코어를 계산할 수 있게 됩니다. 아래 그림은 위에서 설명했던 실험 세팅에서 30차원 대신 3차원을 사용했을 때의 IF와 RRCF의 이상 스코어 값을 나타냅니다. (확대해서 보시길 바랍니다.)

인위 데이터 2. 실시간 스트리밍 데이터
두 번째 실험은 본 포스팅 서두에 있는 그림에 대한 실험입니다. 데이터는 아래 코드를 사용하여 생성되었습니다. 요컨데, 730일의 기간동안 사인함수를 따르는 신호가 기록되어 있고, 235일부터 255일까지는 이상 신호가 발생한 것으로 이해하시면 됩니다.
# 출처: 참고문헌 [5]
n = 730
A = 50
center = 100
phi = 30
T = 2 * np.pi / 100
t = np.arange(n)
sin = A * np.sin(T * t - phi * T) + center
sin[235:255] = 80
이 실험에서 두 가지 중요한 점은
- 730일의 데이터가 한번에 주어지는 것이 아니라, 하루에 하나씩 데이터가 들어오는 실시간 스트리밍 데이터 환경을 가정한다는 것과
Shingling이라는 방법을 사용하여 1차원 데이터를 4차원 데이터로 바꿔준 후RRCT를 만든다는 것입니다.Shingling은 최근 $k$개의 값을 열벡터로 결합하여 feature 벡터로 사용하는 방법입니다. 예를 들어, 크기 $4$shingling을 사용할 경우, 첫 번째 데이터는 $(t_1, t_2, t_3, t_4)^T$, 두 번째 데이터는 $(t_2, t_3, t_4, t_5)^T$, $\cdots$ , 이런 식으로 데이터가 구성됩니다.- 시계열 데이터 분석에서 자주 사용되는 방법입니다. 다른 이름으로도 많이 불립니다.
실시간 스트리밍 데이터 환경에서는 데이터가 하나씩 들어올 때마다 num_tree개의 모든 RRCT에 데이터를 추가해줍니다. 그러다가 트리의 사이즈가 tree_size에 도달하면 가장 과거의 데이터를 제거해주고 새로운 데이터를 추가하는 방식으로 Forest를 유지하게 됩니다. 논문에서는 num_tree의 값으로 100을, tree_size의 값으로 256을 사용하였습니다. 실험 결과 그림은 본 포스팅 서두에 있기 때문에 생략하도록 하겠습니다. 중요한 점은 RRCF는 실시간 스트리밍 데이터에 적합한 알고리즘이 있으며, 이상 신호의 시작을 포착하는데 탁월하다는 것입니다.
실제 데이터 1. 뉴욕시 택시 탑승객 수 데이터
마지막 실험은 “뉴욕시 택시 탑승객 수” 데이터셋에 RRCF를 적용한 실험입니다. 해당 데이터셋은 비지도 학습 이상감지 분야에서 자주 사용되는 벤치마킹 데이터셋 Numenta Anomaly Benchmark (NAB) 데이터셋 중 하나입니다. 데이터셋에는 2014년 7월부터 2015년 1월까지의 뉴욕시 택시 탑승객 수가 30분 단위로 저장되어 있습니다. 원래는 레이블이 없는 데이터셋이지만 논문에서는 연휴나 기념일 등 총 8개의 이벤트를 이상신호로 간주하여 정량적인 평가도 더했습니다. 이때, 해당 일에 포함되는 데이터 모두 (하루에 48개)를 이상 데이터로 레이블링 했습니다.
- Independence Day (2014-07-04 ~ 2014-07-06)
- Labor Day (2014-09-01)
- Labor Day Parade (2014-09-06)
- NYC Marathon (2014-11-02)
- Thanksgiving (2014-11-27)
- Christmas (2014-12-25)
- New Years Day (2015-01-01)
- North American Blizard (2015-01-26 ~ 2015-01-27)
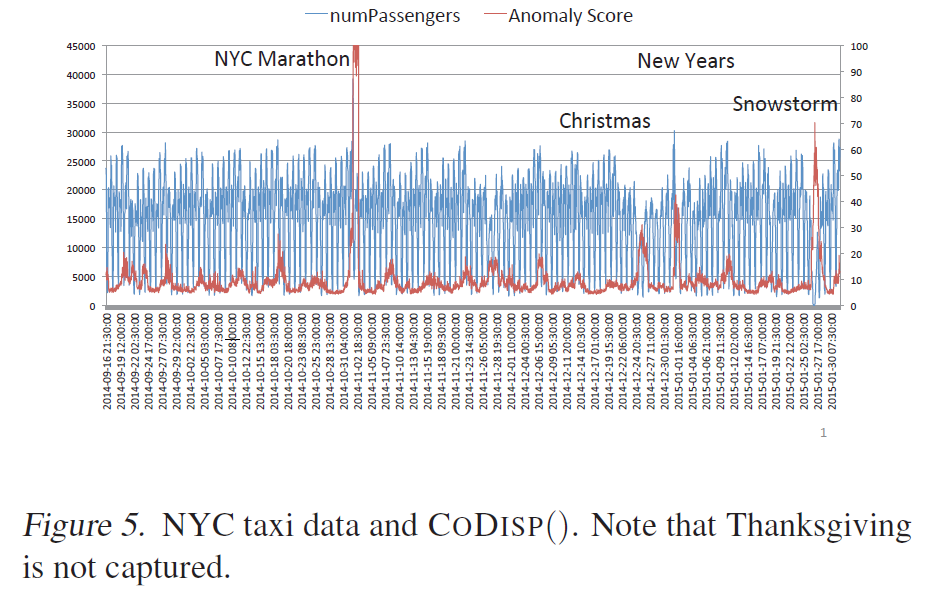
이 데이터셋 역시 시계열 데이터이기 때문에 사이즈 48의 shingling을 사용했습니다. 즉, 과거 48개 (총 24시간)의 탑승객 수를 결합하여 하나의 데이터를 만든 것입니다. 그리고 이 실험 역시 실시간 스트리밍 데이터 환경을 가정하고 진행하였습니다. 논문에서는 num_tree의 값으로 200을, tree_size의 값으로 1000을 사용하였습니다. 아래 그림은 결과 그림입니다. 파란색 선은 탑승객 수를, 빨간색 선은 이상 스코어를 나타냅니다. 몇 가지 주요 이벤트에 대해서 높은 이상 스코어를 보이는 것을 확인할 수 있습니다. 한 가지 유의할 점은 2014년 7월 14일부터 2014년 9월 15일까지의 결과가 없다는 점입니다. 2014년 9월 16일부터는 총 5개의 이상 이벤트가 있었는데, Thanksgiving을 제외하고 나머지 4개 이벤트를 성공적으로 탐지해냈습니다.
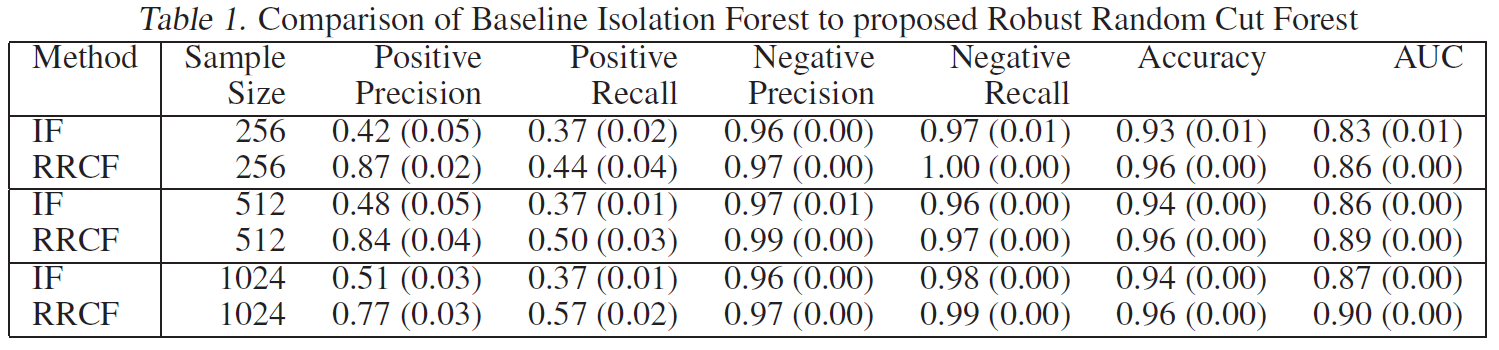
아래의 표는 IF와 RRCF 모델의 정량적인 평가를 나타냅니다. IF 모델에 대해서는 논문의 저자가 스스로 실시간 스트리밍 환경 버전을 만들어서 사용했는데, 그 방법이 다소 많이 나이브합니다. 그 점이 IF의 성능 지표가 낮은 이유일 수도 있습니다. 그 점을 감안하고 봐주시면 좋을 것 같습니다. 여러 평가지표 중에 RRCF는 특히 precision에서 큰 차이를 만들어 냈습니다. 이는 모델이 이상 데이터라고 예측한 것들 중에 실제로 맞춘 비율이 높다는 것을 의미합니다. 다르게 표현하면 모델이 잘못된 경보를 보낸 비율이 작다는 의미입니다.
마지막 표는 이벤트 단위로 점수를 매긴 것입니다. 하나의 이벤트는 1일에서 길게는 3일로 구성되어 있습니다. 그리고 하루마다 30분 단위로 48개의 데이터가 기록됩니다. 위의 표는 이 30분 단위 데이터마다 정상/이상을 예측하여 평가지표를 계산한 것입니다. 아래의 표는 그것이 아니라 이벤트 단위로 이상 감지에 성공했는지를 나타내는 표라고 생각하시면 될 것 같습니다. 이 표에서 주목할 점은 Time to detect onset/end 입니다. Time to detect onset/end 는 각각 이벤트를 이상 데이터라고 감지하기 시작한 시점과 종료한 시점입니다. 30분 단위인 것을 고려하면, IF는 이벤트 발생 후 평균적으로 약 11시간만에 이상 데이터라고 예측을 했습니다. 반면, RRCF는 이벤트 발생 후 평균적으로 약 7시간만에 이상 데이터라고 예측을 한 것을 확인할 수 있습니다. 이상 감지까지 너무 오랜 시간이 걸렸다고 생각이 들 수 있습니다. 하지만 휴일 또는 행사 날짜가 되자마자 택시 탑승객 수가 눈에 띄게 바뀌는 것은 아닐 것이기 때문에 꽤 빠르게 감지한 것으로 볼 수 있을 것 같습니다.

재야의 숨은 초보의 한 마디
개인적으로 논문에 사용되는 단어나 문장이 극도로 어려워서 읽기 어려웠던 논문입니다. 저자가 이유를 생략하고 결과만 말하는 경우도 많아서 스스로 생각해봐야 하는 시간도 많이 필요했습니다. 하지만, 이 논문은 볼 수록 매력 있는 볼매 논문인 것 같습니다. 처음에 이해되지 않았던 내용들을 코드까지 봐가면서 조금씩 이해하게 되었는데, 그 때마다 논문의 아이디어가 정말 매력적이란 것을 느꼈습니다. 본 포스팅이 누군가에게 논문을 이해하는데에 한 줄기라도 도움이 되었다면 저는 그것으로 만족합니다.
이상으로 Robust Random Cut Forest Based Anomaly Detection On Streams 논문 먹방을 마치도록 하겠습니다. 정말 긴 글 읽어주셔서 감사합니다.
참고문헌
[1] S. Guha, N. Mishra, G. Roy, O. Schrijvers, "Robust Random Cut Forest: Based Anomaly Detection on Streams", Proceedings of The 33rd International Conference on Machine Learning, 48, pp. 2712-2721, 2016.
[2] F. T. Liu, K. M. Ting and Z. Zhou, "Isolation Forest," 2008 Eighth IEEE International Conference on Data Mining, 2008, pp. 413-422, doi: 10.1109/ICDM.2008.17.
[3] 고려대학교 강필성 교수님의 강의 영상, https://youtu.be/puVdwi5PjVA
[4] 산업수학 및 수학적 데이터 분석 방법 소개 및 개선된 RCF를 활용한 센서 데이터 이상 감지 문제 해결 사례, 국가수리과학연구소 (NIMS) 산업수학혁신센터 김민중 박사, 2021년 POSTECH SIAM Student Chapter Summer School의 기조강연 중
[5] 파이썬 rrcf 패키지 공식 문서 (https://klabum.github.io/rrcf/)

