
이번 포스팅에서는 Twin Delayed Deep Deterministic policy gradient algorithm (TD3)가 어떻게 DDPG를 개선했는지 짧게 요약해볼 것이다. TD3는 다음 세 가지를 사용해서 function approximation error의 안 좋은 효과를 완화시켰다. 여기서 안 좋은 효과는 overestimation 편향, 추정값에 대한 큰 분산 등을 의미한다.
- Clipped double Q-learning
- Delayed policy updates
- Target policy smoothing regularization
본 포스팅에서는 위 세 가지만 간략히 정리할 예정이다. 논문에서는 위 세 가지 기술의 motivation으로서 function approximation error, overestimation, large variance를 심도 있게 다루고 있으니 관심 있는 분들은 논문을 꼭 읽어보는 것을 권장한다.
- 제목: Addressing Function Approximation Error in Actor-Critic Methods
- 저자: Fujimoto, Scott, Herke van Hoof, David Meger, McGill University
- 연도: 2018
- 링크: https://proceedings.mlr.press/v80/fujimoto18a.html
Clipped double Q learning
Q learning은 어떤 행동의 가치를 과추정 (overestimation) 하게 되면, 정책이 과추정한 행동을 선호하게 되고, 이는 다시 행동의 가치를 추정하는데 편향을 부여하는 경향이 있다. Q learning의 TD target은 다음과 같다. \[y = r + \gamma \max_{a'}Q(s', a')\]
Double Q learning은 두 개의 행동가치함수를 만들어서, 한 행동가치함수의 업데이트에 필요한 TD target을 다른 행동가치함수로부터 계산하는 방법으로 overestimation을 완화시킨다. Double Q learning에는 2개의 critics이 있으며, 각각을 업데이트하기 위한 TD target을 다음과 같이 계산하게 된다. \[\begin{matrix} Q_{1}(s, a) & \leftarrow & r + \gamma Q_2 \left(s', \operatorname*{argmax}\limits_{a'}Q_1(s', a') \right) \\ Q_{2}(s, a) & \leftarrow & r + \gamma Q_1 \left(s', \operatorname*{argmax}\limits_{a'}Q_2(s', a') \right) \end{matrix}\]
식을 풀어 설명하자면, $Q_1(s, a)$ 업데이트를 위한 타겟을 계산할 때, 다음 상태 $s’$에서 행동가치함수 값이 가장 큰 행동 $\operatorname{argmax}_a Q_1(s’, a’)$의 행동가치함수 값을 $Q_2$로부터 계산하게 된다. DDPG에 double Q learning를 적용한다면 TD target은 다음과 같은 형태가 될 것이다. \[\begin{matrix} y_1 & = & r + \gamma Q_{\theta_2'} \left(s', \pi_{\phi_1'}(s') \right) \\ y_2 & = & r + \gamma Q_{\theta_1'} \left(s', \pi_{\phi_2'}(s') \right), \end{matrix}\]
이때, 정책 $\pi_{\phi_1}, \pi_{\phi_2}$은 각각 $Q_{\theta_1}$과 $Q_{\theta_2}$를 사용하여 학습된 정책이다. 매개변수 $\phi, \theta$는 각각 정책과 critic의 매개변수이고, $\phi’, \theta’$은 각각 target 정책과 target critic의 매개변수이다. 이러면 $Q_{\theta_1}$을 최대화하는 방향으로 학습된 정책 $\pi_{\phi_1}$의 행동가치함수가 $Q_{\theta’_2}$에 의해 계산된다. 따라서 $Q_{\theta_1}$의 overestimation 편향으로 발생한 정책 $\pi_{\phi_1}$의 편향은 완화될 수 있을 것이다. 하지만 만약 운이 좋지 않아서 $Q_{\theta’_2}$에도 overestimation이 포함되어 있다면, 그것이야 말로 큰일이다.
그래서 TD3 논문에서는 그냥 이럴 바엔 overestimation 대신 underestimation 되는 것을 선택한다. 근거 없는 자신감으로 허세를 부릴 바에는, 자신을 낮게 내려쳐 겸손해지는 방법을 선택한 것이다. clipped double Q learning은 다음과 같이 TD target을 계산한다. \[y_1 = r + \gamma \min\limits_{i=1, 2} Q_{\theta_i'}(s', \pi_{\phi_1'}(s'))\]
Double Q learning에서는 정책 $\pi_{\phi_1}$이 $Q_{\theta_1}$으로부터 업데이트 되었기 때문에 이와 독립적일 수 있는 $Q_{\theta_2’}$로 평가를 받았다. 하지만, 이제 정책 $\pi_{\phi_1}$은 $\min_{i=1,2}Q_{\theta_i}$ 함수로 평가를 받게 된다. 따라서 이제 독립성을 위해 정책 2개를 사용할 필요가 없어졌다. 독립성이고 뭐고 그 값이 더 작은 아이를 선택할 것이기 때문이다. 따라서 TD3 논문에서는 한 개의 정책 $\pi_{\phi}$가 있으며, $\pi_{\phi}$은 $Q_{\theta_1}$을 사용하여 업데이트 된다.
Target policy smoothing regularization
Clipped double Q learning을 사용하여 TD target을 계산하는 과정은 다음과 같다. 먼저 다음 상태 $s’$을 target policy $\pi_{\phi’}$에 입력하여 다음 행동 $\tilde{a}$을 구한다. \[\tilde{a} = \pi_{\phi'}(s').\]
다음으로 두 개의 target critics 값 $Q_{\theta_1’}(s’, \tilde{a})$와 $Q_{\theta_2’}(s’, \tilde{a})$ 중 작은 값을 사용하여 TD target을 만든다. \[y = r + \gamma \min\limits_{i=1, 2} Q_{\theta_i'}(s', \tilde{a})\]
이 TD target을 사용해서 두 critics $Q_{\theta_1}(s, a)$와 $Q_{\theta_2}(s, a)$를 업데이트하게 된다.
이때 target policy $\pi_{\phi’}$는 function approximation error를 포함하고 있을 수 있다. 예를 들면, 정책이 critic $Q_{\theta_1}$의 불안정한 지형에 과적합되어 있을 수도 있다. 그렇게 되면 $s’$ 주위에서 $\pi_{\phi’}$ 값이 엄청 들쭉 날쭉할텐데, $\pi_{\phi’}(s’)$ 값 하나에만 의지하여 TD target을 만든다면 TD target의 분산이 증가하여 학습을 저해할 수 있다.
이 논문에서는 TD target의 분산을 줄이기 위한 방법으로 target policy smoothing regularization을 제안했다. $\pi_{\phi’}(s’)$ 값 하나에만 의존하지 않고, $\pi_{\phi’}(s’)$의 주변 행동의 가치함수의 기댓값을 사용하여 TD target을 만드는 방법이다. 즉, \[y = r + \gamma \mathbb{E}_{\epsilon} \left[ Q_{\theta'} \left(s', \pi_{\theta'}(s') + \epsilon \right) \right].\]
이 방식은 expected SARSA를 연상시킨다. 기존 SARSA의 TD target은 $y=r + \gamma Q(s’, a’)$이다. 이때, $a’$은 에피소드 진행하는 동안 선택했던 행동이다. 이 $a’$ 하나에만 의지하여 TD target을 계산하는 대신 모든 행동에 대한 행동가치함수의 기대값을 사용하는 것이 expected SARSA이다. 즉, Expected SARSA의 TD target은 $y = r + \gamma \mathbb{E}_{a’}\left[ {Q(s’, a’)} \right]$이다.
구현에서는 기댓값을 구하는 대신 그냥 그때 그때 $\pi_{\phi’}(s’)$에 노이즈를 추가하는 방식으로 진행된다. 가우시안 분포에서 노이즈를 샘플링 후 $-c$와 $c$ 사이로 값을 제한하여 사용하게 된다. 실험에서는 $\tilde{\sigma}=0.2, c=0.5$를 사용한다. \[\tilde{a} = \pi_{\phi'}(s') + \epsilon, \; \text{ where } \epsilon \sim \text{clip}(\mathcal{N}(0, \tilde{\sigma}), -c, c).\] \[y = r + \gamma \min\limits_{i=1,2}Q_{\theta_i'}(s' ,\tilde{a})\]
Delayed policy update
논문에서 이쪽 분량이 꽤 많은데, 한줄로 요약할 수 있을 것 같다. Delayed policy update는 매 timestep마다 policy와 critic을 업데이트하지 않고, critic이 먼저 충분히 수렴한 후에 policy를 업데이트하는 방법이다.
우리는 일관성 있는 TD target을 제공하기 위해 target critics / target policy를 사용한다. 하지만 TD target이 고정되어 있더라도, gradient descent는 여러 iteration 동안 TD error를 서서히 감소시킨다. TD error가 큰 critic을 사용해서 정책을 업데이트하면 당연스럽게도 정책 업데이트도 잘 안 될 것이다. 그래서 TD error가 충분히 감소된 critics을 사용해서 정책을 업데이트하자는 것이 delayed policy update의 취지이다.
TD3 알고리즘에서는 두 critics는 매 timestep 업데이트되고, policy, target policy, target critics는 매 $d$번마다 업데이트된다. 실험에서는 $d=2$를 사용한다. 이로 인해 총 policy를 업데이트하는 횟수가 절반으로 줄어들게 되는데도 성능이 굉장히 좋다.
알고리즘

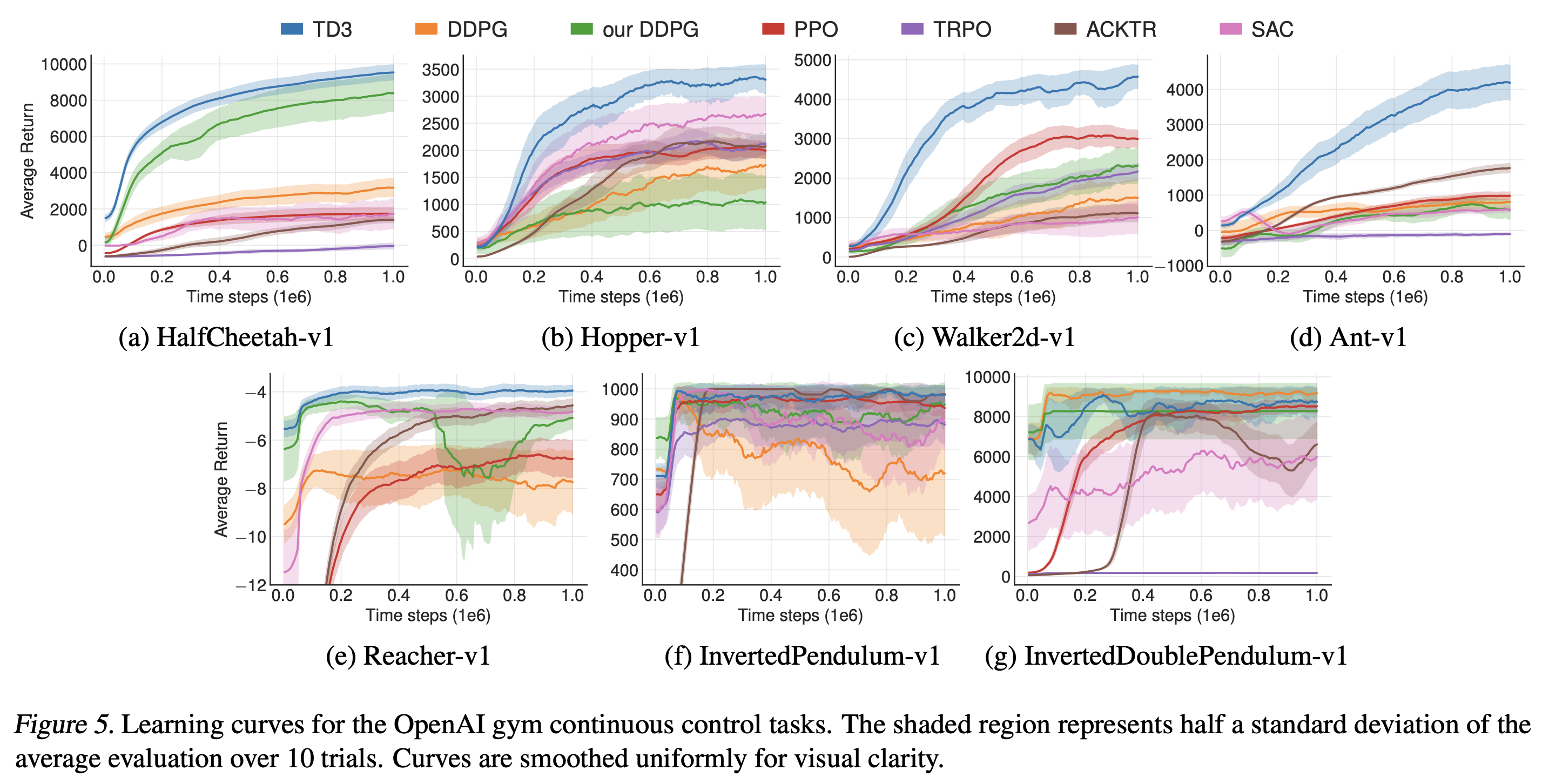
실험
- Adam with a learning rate of 0.0001
- Batch size: 100
- Policy exploration: $\epsilon \sim \mathcal{N}(0, 0.1)$
- Target policy smoothing: $\epsilon \sim \text{clip}(\mathcal{N}(0, 0.2), -0.5, 0.5)$
- Delayed policy update: $d=2$
- Soft target network update: $\tau=0.005$
- 환경마다 처음 10,000 또는 1,000 timesteps 동안 a purely exploratory policy 사용
- 환경과 에이전트마다 총 10개의 seed에 대해서 실험하고 평균 및 표준편차를 보고.
- 매 seed마다 총 1,000,000 timesteps, 매 5,000번마다 평가하며 10번 에피소드의 평균 return 값 보고
참고 문헌
Fujimoto, Scott, Herke van Hoof, and David Meger. “Addressing Function Approximation Error in Actor-Critic Methods.” In Proceedings of the 35th International Conference on Machine Learning, edited by Jennifer Dy and Andreas Krause, 80:1587–96. Proceedings of Machine Learning Research. PMLR, 2018. https://proceedings.mlr.press/v80/fujimoto18a.html.

