
지난 포스팅에서는 TRPO 논문의 스토리에 대해서 심도 있게 다뤄보았다. TRPO는 일반적인 정책에 대해서 정책의 monotonic improvement를 보장할 수 있는 방법을 이론과 함께 제시하였다. 하지만, 이론이 복잡할수록 구현은 어려운 법이다. 유명 강화학습 라이브러리에서도 TRPO의 구현체가 없는 것을 보면 TRPO는 구현이 어렵다는 것을 간접적으로 알 수 있다. 내 생각에 TRPO에서 중요한 부분은 현재 정책과 “가까운 정책들 중에서” performance measure를 최적화하는 정책을 찾는 것이다. 이는 performance measure를 최적화하는 방향을 먼저 찾고, 그 방향으로 정책을 아주 조금만 업데이트하면 어느 정도 위의 사항을 달성할 수 있다. PPO는 TRPO의 업데이트 크기를 clip하여 정책을 조금씩만 업데이트 하는 방법이라고 요약할 수 있다.
- 제목: Proximal Policy Optimization Algorithms
- 저자: John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, Oleg Klimov, Open AI
- 연도: 2017
- 링크: https://arxiv.org/abs/1707.06347
다음 링크에서 본 포스팅의 PDF 파일 버전을 다운 받아서 볼 수 있습니다.
TRPO의 목적함수
TRPO는 업데이트 전 정책 $\pi_{\theta_{\text{old}}}$와 업데이트 후 정책 $\pi_{\theta}$의 KL divergence에 대해 제약 (constraint)을 걸어 다음 surrogate objective를 최대화를 했다. \[\operatorname*{maximize}_\theta \hat{\mathbb{E}}_t \left[ \frac{\pi_{\theta}\left( a_t |s_t\right)}{\pi_{\theta_{\text{old}}}\left( a_t |s_t\right)} \hat{A}_t\right], \quad \quad (1)\] \[\text{subject to} \quad \hat{\mathbb{E}}_t \left[ \operatorname{KL}\left[ \pi_{\theta_{\text{old}}}\left(\cdot|s_t \right), \pi_\theta \left(a_t | s_t \right) \right] \right] \le \delta. \quad \quad (2)\]
해석하자면,
- 정책은 주어진 상태에 대한 행동들의 확률분포이기 때문에 두 정책 사이의 KL divergence를 계산할 수 있다.
- 업데이트 전, 후 정책의 KL divergence를 $\delta$ 이하로 유지하면서 식 $(1)$의 surrogate objective를 최대화.
- TRPO에서는 식 $(1), (2)$의 constraint optimization 대신 아래의 $(3)$을 최대화하는 방법도 제안했지만, $\beta$ 값을 하나로 정하는 것이 매우 어렵다고 한다. $\beta$를 환경에 따라 지정해줘야할 뿐만 아니라, 사실 학습 도중에도 adaptive하게 바꿔줘야할 필요가 있었다.
논문의 해결책
Clipped Surrogate Objective
- KL divergence를 이용하여 업데이트의 크기를 제한하지 않고, 애초에 업데이트 대상인 $\frac{\pi_{\theta}\left( a_t |s_t\right)}{\pi_{\theta_{\text{old}}}\left( a_t |s_t\right)} \hat{A}_t$의 크기를 clipping하여 제한.
- 표기의 편의를 위해 $r_{t} \left( \theta \right) = \frac{\pi_{\theta} \left( a_t | s_t \right)}{\pi_{\theta_{\text{old}}} \left( a_t | s_t \right)}$라 하자. (진작에 할껄 ,,,)
where \[\operatorname{clip}\left(x, \text{low}, \text{high} \right)=\begin{cases} \text{low} & \text{if } x<\text{low} \\x & \text{if } \text{low} \le x < \text{high} \\ \text{high} & \text{if } x \ge \text{high} \end{cases}\]
- 우선 $\theta = \theta_{\text{old}}$일 때 $r_t \left( \theta \right)=1$에서 업데이트를 시작한다.
- 만약 $\hat{A}_t>0$ 라면, 상태 $s_t$에서 행동 $a_t$를 취할 확률을 높여주는 방향으로 policy를 업데이트하게 된다. 따라서 $r_t \left( \theta \right)$이 1보다 커지게 된다. 이때, $\operatorname{clip}$은 $r_t \left( \theta \right)$이 $1+\epsilon$ 까지만 커지도록 만들어준다.
- 반대로 만약 $\hat{A}_t<0$ 라면, 상태 $s_t$에서 행동 $a_t$를 취할 확률을 낮춰주는 방향으로 policy를 업데이트한다. 즉, $r_t \left( \theta \right)$이 1보다 작아지게 된다. 이때, $\operatorname{clip}$은 $r_t \left( \theta \right)$이 $1-\epsilon$ 까지만 작아지게 만들어준다.
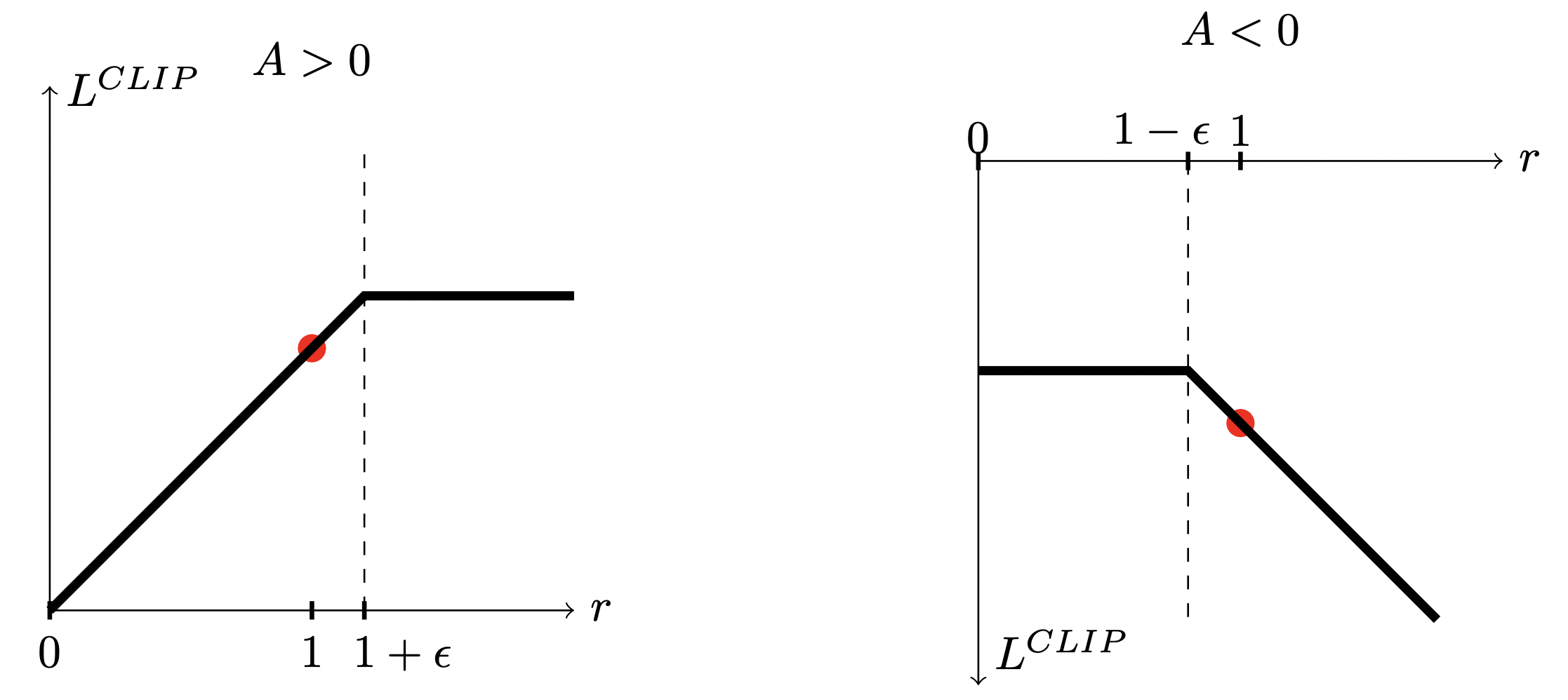
Adpative KL Penalty Coefficient
Clipped surrogate objective 방법 대신 식 $(3)$의 $\beta$를 policy가 업데이트 정도에 따라 adaptive하게 바꿔주는 방법인데, 굳이 정리할 필요까지는 없는 듯 ..?
전체 목적 함수
우선 Advantage에 대한 추정량 (estimator)는 다음과 같다. \[\hat{A}_{t} = \delta_{t} + (\gamma\lambda)\delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\delta_{T-1}, \quad \quad (5)\] \[\text{where} \quad \delta_t=r_t+\gamma V(s_{t+1}) - V(s_t). \quad \quad (6)\]
$\lambda=1$일 때를 살펴보면 조금 와닿는다. \[\hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + \cdots + \gamma^{T- t +1}r_{T-1}+\gamma^{T-t} V(S_T)\]
우리가 아는 advantage $A_t = Q(s_t, a_t) - V(s_t)$과 식 $(6)$을 비교해보면 $-V(s_t)$는 동일하게 갖고 있으며, 나머지 텀 $r_{t} + \gamma r_{t+1} + \cdots + \gamma^{T-t+1}r_{T-1} + \gamma^{T-t} V(S_T)$는 $Q(s_t, a_t)$를 추정량이다. 이 논문에서 제안하는 전체 목적 함수는 다음과 같다. \[L_{t}^{\text{CLIP}+\text{VF}+\text{S}}\left( \theta \right) = \hat{\mathbb{E}}_t \left[ L_t^{\text{CLIP}} \left( \theta \right) -c_{1}L_{t}^{\text{VF}}\left( \theta \right) + c_{2} S\left[\pi_{\theta}\right]\left( s_{t} \right)\right], \quad \quad (7)\]
where $L_t^{\text{VF}} \left( \theta \right) = \left( V_{\theta} \left( s_{t} \right) - V_{t}^{\text{targ}} \right)^{2}$으로 가치 함수 approximator를 훈련시키기 위한 텀이다. $S\left[\pi_{\theta} \right] \left( s_t \right)$은 entropy bonus으로서 exploration을 하게 만들어주는 텀이다. $c_1, c_2$는 각 텀에 대한 가중치이다.
Algorithm
- 요약: $N$개의 policy가 각각 병렬적으로 환경과 $T$번 상호작용하여 $NT$개의 경험 데이터 획득하고, 이 경험 데이터들을 사용하여 목적 함수 최적화

Experiment
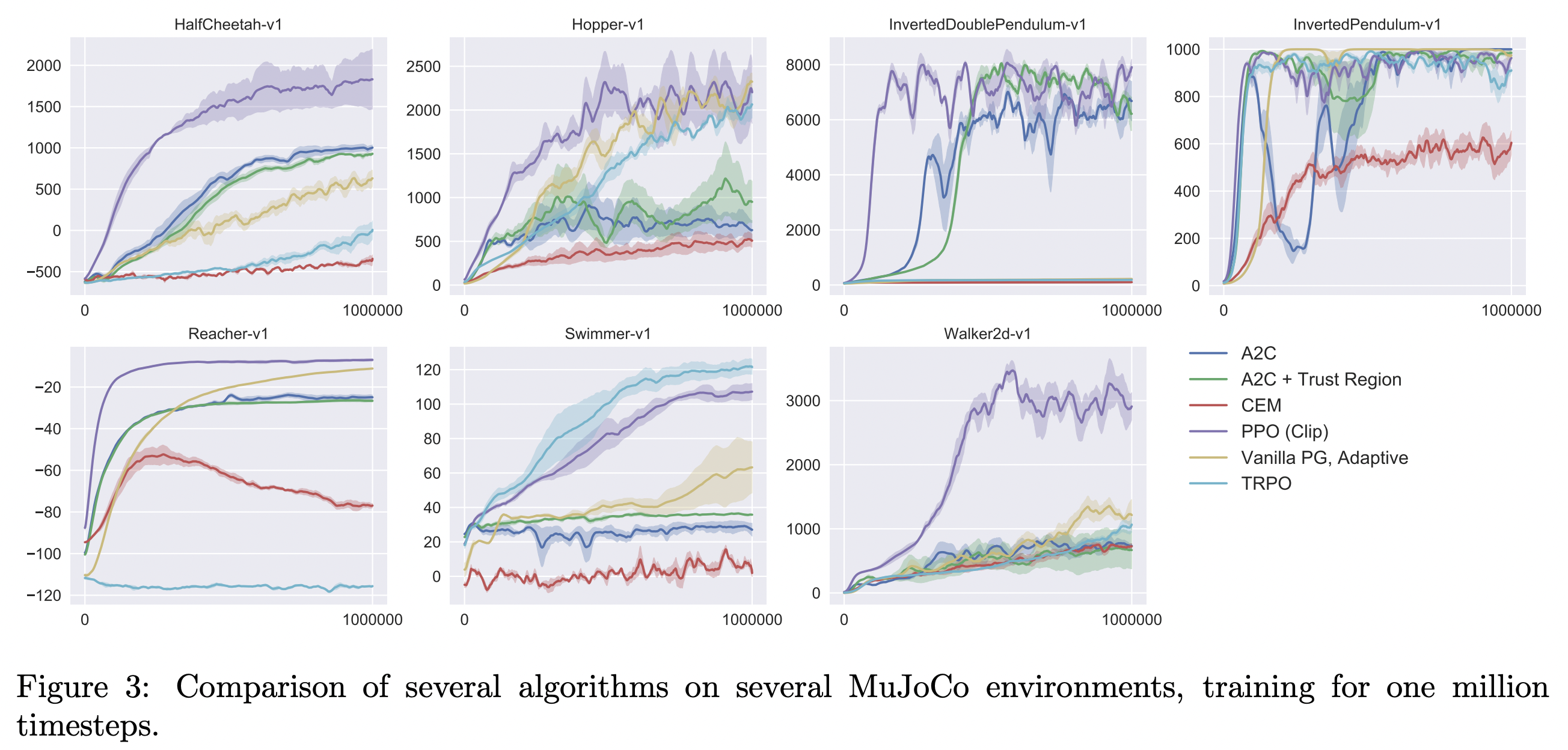
Experimental setting
- HalfCheetah, Hopper, InvertedDoublePendulum, InvertedPendulum, Reacher, Swimmer, Walker2d, all “-v1”, OpenAI Gym.
- Policy network: a MLP with two hidden layers of 64 units, tanh nonlinearities, outputting the mean of a Gaussian distribution, with variable standard deviations.
- No parameter sharing between policy and value function
- No entropy bonus
- Train for 1 million timesteps
- $\gamma=0.99, \lambda=0.95$
참고 문헌
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv. https://doi.org/10.48550/arXiv.1707.06347

