AdamWR에 대해 알아보자!
"Decoupled weight decay regularization 논문 리뷰 (2)"
"Decoupled weight decay regularization 논문 리뷰 (2)"
AdamW를 소개하는 논문 “Decoupled weight decay regularization” 논문에는 AdamW 이외에도 AdamWR 이라는 최적화 알고리즘을 소개하고 있다. AdamWR은 저자의 이전 논문에서 소개한 warm restart with cosine annealing을 AdamW에 적용한 최적화 알고리즘이다.
AdamWR을 이해하기 위해서는 learning rate annealing과 warm restarts가 무엇인지 그리고 왜 사용되는지 알아야하기 때문에 이렇게 따로 2부를 준비해보았다. 글의 대부분은 A Newbie’s Guide to Stochastic Gradient Descent With Restarts을 참고하여 작성하였다.
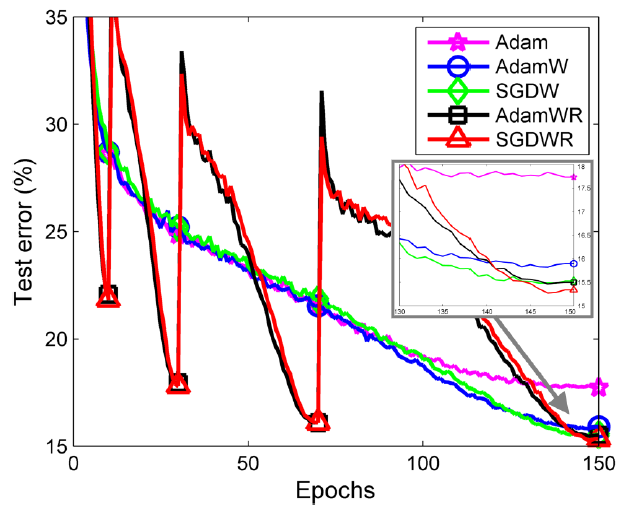
위 사진은 내 마음대로 선정한 2부의 메인 figure이다. ImageNet32x32 Top5 테스트 에러를 나타내는 learning curve이고, Adam. AdamW, SGDW, AdamWR, SGDWR 순서로 성능이 좋은 것을 알 수 있다. warm restart를 사용하는 AdamWR, SGDWR의 경우 테스트 에러가 학습 중간중간 폴짝 뛰는 모습을 보이는데, 이것은 학습 중간중간에 learning rate를 점프시키기 때문이다. 이 작용으로 AdamWR과 SGDWR은 일반화를 더 잘하는 local minimum을 찾을 수 있다.
들어가기 전에
- 이 post에서 언급하는 SGD는 momentum을 포함한 SGD 이다.
- 이 post는 2부로 나누어서 포스팅할 예정이다.
이 포스트에서 다룰 내용들
- Learning rate schedule과 Learning rate annealing
- step-drop learning rate decay
- linearly decreasing learning rate decay
- cosine annealing
- Warm restart
- Normalized weight decay
Learning rate schedule 과 Learning rate annealing
Learning rate schedule란 단어 그대로 훈련 동안에 고정된 learning rate를 사용하는 것이 아니고 미리 정한 스케줄대로 learning rate를 바꿔가며 사용하는 것이다. 그리고 learning rate annealing은 learning rate schedule과 혼용되어 사용되지만 특히, learning rate가 iteration에 따라 monotonically decreasing하는 경우를 의미하는 것 같다. 참고로 anneal의 뜻은 “담금질하다”이다. 따라서 Learning rate annealing을 해석하면 “학습률 담금질하기” 정도가 되겠는데 쉽게 와닿지 않기 때문에 별도로 해석해서 사용하지 않는 편이 좋을 것 같다. Learning rate annaeling을 사용하면 초기 learning rate를 상대적으로 크게 설정하여 Local minimum에 보다 더 빠르게 다가갈 수 있게 만들어주고 이후 learning rate를 줄여가며 local minimum에 보다 더 정확하게 수렴할 수 있게 만들어준다.
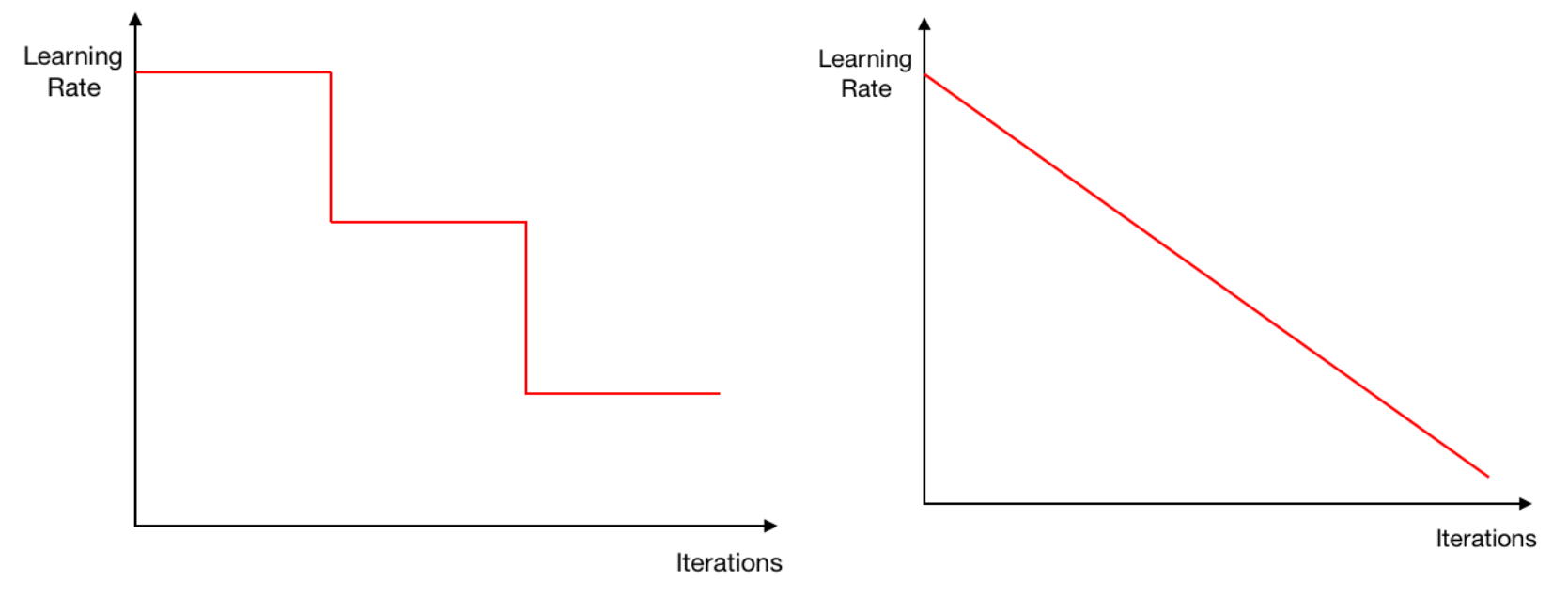
Learning rate annealing에는 다양한 방법이 있을 수 있다. 가장 쉬운 예로, 위의 왼쪽 그림처럼 learning rate를 학습이 진행됨에 따라 step function 처럼 감소시킬 수 있다. 이를 step-drop learning rate decay라고 한다. 또는 오른쪽 그림처럼 학습이 진행됨에 따라 learning rate를 선형적으로 감소시킬 경우 linearly decreasing learning rate decay라고 한다. 그리고 최근에 많이 사용되는 cosine annealing은 아래 그림처럼 half-consine 그래프를 따라 learning rate를 감소시킨다.
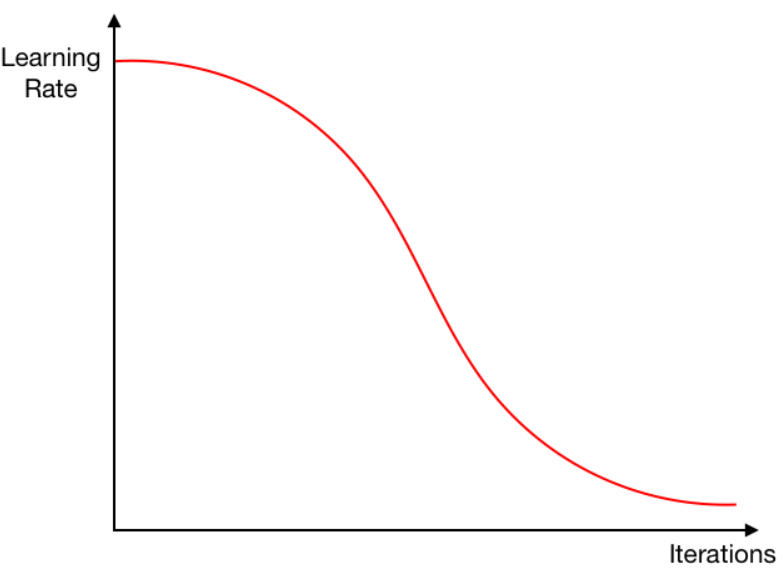
직관적으로는 처음에는 높은 learning rate로 좋은 수렴 지점을 빡세게 찾고, 마지막에는 낮은 learning rate로 수렴 지점에 정밀하게 안착할 수 있게 만들어주는 역할을 할 것 같다. 여기까지가 learning rate annealing에 대한 설명이다. 복습하자면 learning rate annealing은 iteration에 따라 learning rate를 감소시켜주는 방법이다. 하지만 훈련 도중 learning rate를 증가시켜주는 learning rate schedule을 사용할 수도 있다. 앞으로 다룰 warm restart도 학습 중간중간 learning rate를 증가시켜주는 방법이다. 다음으로 warm restart에 대해 알아보자.
Warm restart
좋은 수렴 지점에 대한 직관적 이해
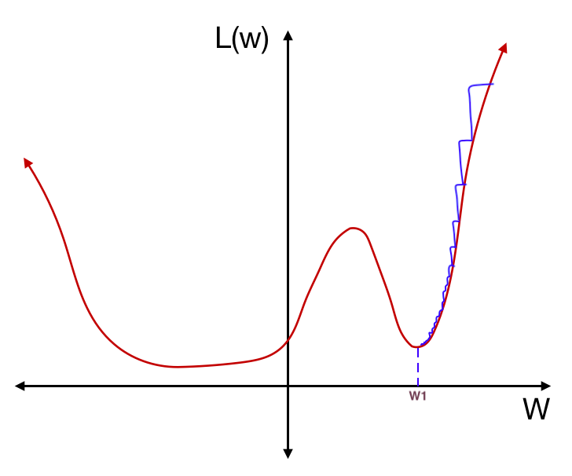
일반화 (generalization) 능력이 좋은 모델은 훈련 데이터의 분포와 조금 다른 분포의 테스트 데이터가 들어와도 역할을 잘 수행할 수 있는 모델이다. 이를 유념하며 직관적인 예시 하나를 살펴보자. 아래 그림처럼 weight에 따른 loss 함수의 그래프가 있다고 하자. 그리고 훈련을 통해 최적의 weight $w_1$을 찾았다고 생각해보자
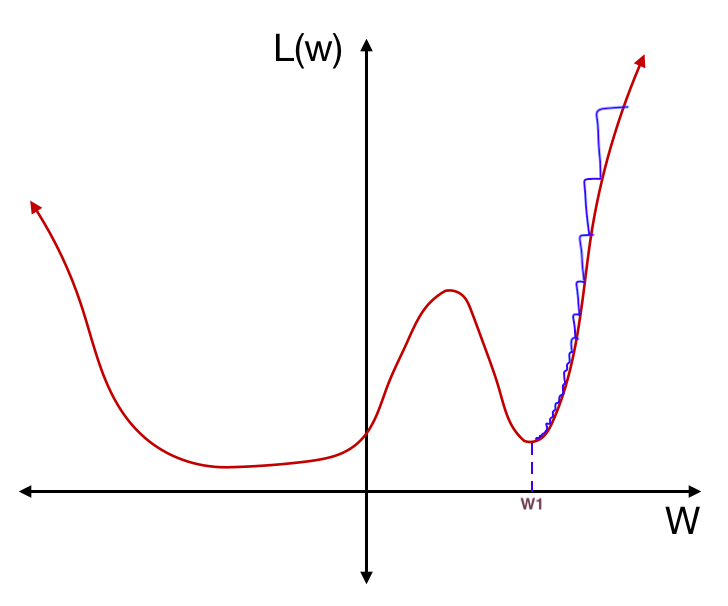
위 그림의 갈색선은 “훈련 데이터로부터 만들어진 weight에 대한 loss 함수”의 그래프이다. “훈련 데이터”로부터 만들어진 loss 함수이기 때문에 훈련 데이터의 분포와 다른 분포의 테스트 데이터에 대해서는 다른 loss 함수가 만들어질 것이다. 예를 들어 아래 그림처럼 테스트 데이터의 분포가 훈련 데이터의 분포와 달라서 다음 그림과 같이 훈련 데이터(살구색)와 테스트 데이터(갈색)의 loss 함수 그래프가 다르게 나타났다고 하자.
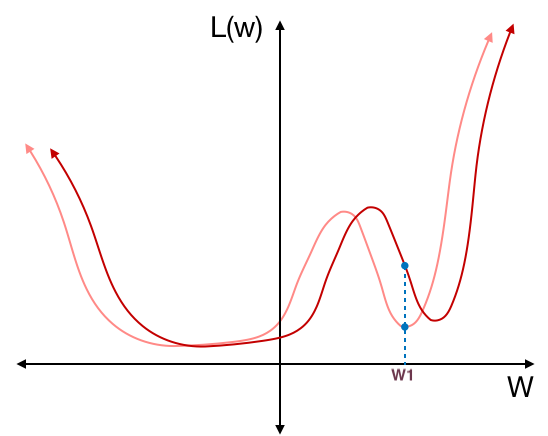
테스트 데이터에 대한 loss 함수는 훈련 데이터에 대한 loss 함수에 비해 아주 조금 달라졌지만, $w_1$에서의 테스트 데이터의 loss는 훈련 데이터의 loss와 굉장히 차이나게 된다. 즉, $w_1$처럼 가파른 local minimum에서는 테스트 데이터의 분포가 조금만 달라져도 error가 민감하게 변한다는 의미이다. 반대로, 모델이 훈련을 통해 최적의 weight를 $w_2$으로 찾았다고 생각해보자.
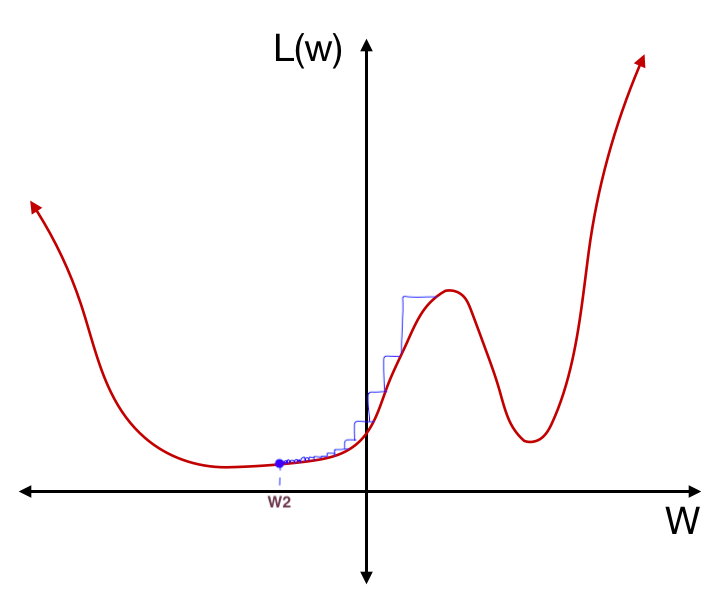
하지만 이 경우 테스트 데이터에 대한 loss 함수가 훈련 데이터에 대한 loss 함수에 비해 달라졌다고 해도 $w_2$에서의 테스트 데이터의 loss는 훈련 데이터의 loss와 크게 달라지지 않는다.
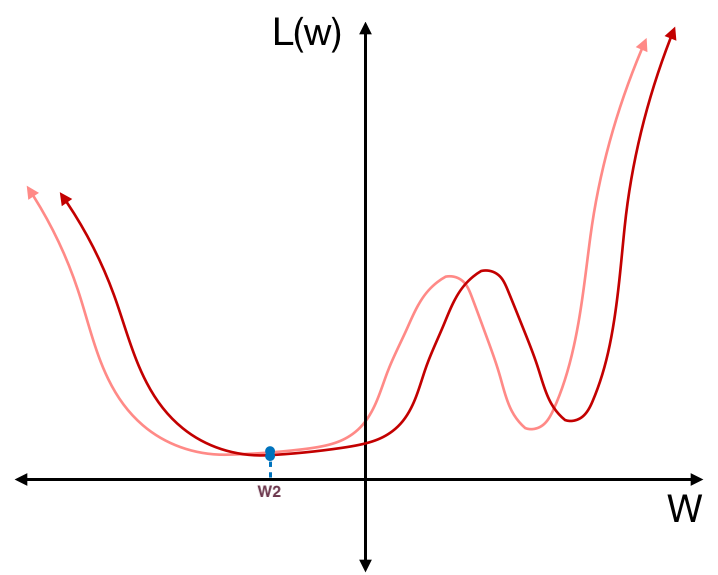
이런 평평한 지점의 weight들은 훈련 데이터의 분포와 다른 테스트 데이터가 들어와도 상대적으로 안정적인 loss 값을 얻을 수 있다. 즉, 보다 더 일반화 (generalized) 되었다고 말할 수 있다.
Warm restart
Warm restart는 위와 같은 문제를 해결하기 위한 한 가지 방법이다. 학습 중간중간에 learning rate를 증가시켜 큰 폭의 weight update를 만들어 가파른 local minimum에서 빠져나올 기회를 제공한다.
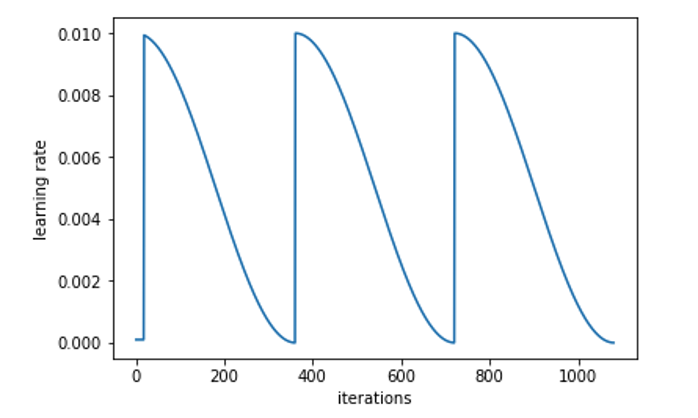
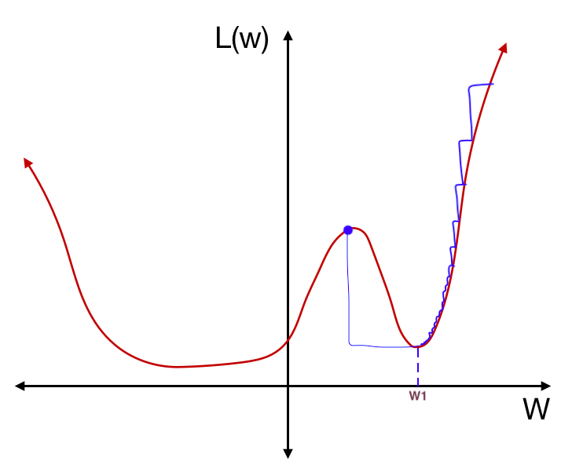
예를 들어 위의 learning rate schedule은 initial learning rate를 0.01로 설정하고 cosine annealing을 사용하며 iteration 380과 iteration 760에서 learning rate를 증가시키는 warm restart이다. 이 learning schedule을 사용하여 다시 한 번 위의 예시를 살펴보자. 먼저 initial weight 지점에서 시작하여 gradient descent를 통해 local minimum $w_1$에 수렴하였다. 업데이트 폭이 점점 줄어드는 것은 cosine annealing을 사용한 것으로 볼 수 있다.
이 때 cosine annealing만 사용하였다면 learning rate가 0에 가까워져 $w_1$에서 weight 업데이트 중지되었을 것이다. 하지만 다시 learning rate를 증가시키면 아래 그림처럼 가파른 local minimum을 탈출할 수 있게 된다. learning rate가 크기 때문에 업데이트 폭도 큰 것을 볼 수 있다.
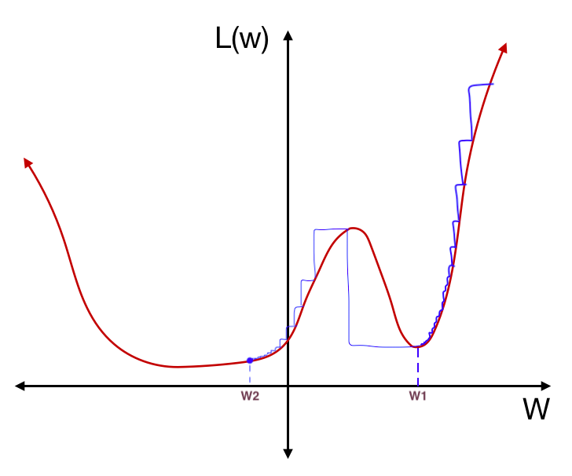
다시 cosine annealing에 따라 learning rate를 줄여가며 gradient descent를 하면 아래 그림처럼 $w_2$으로 가게된다.
learing rate 증가시키는 iteration 지점을 2곳으로 설정했기 때문에 한 번 더 learning rate가 증가되게 된다. 하지만 이번에는 업데이트 폭이 커도 같은 local minimum 안의 weight로 업데이트되게 된다.
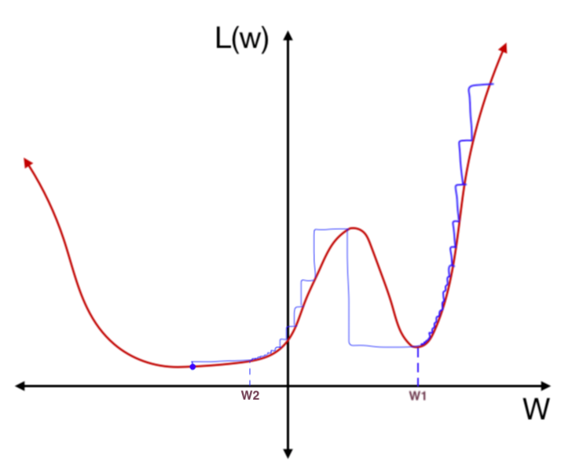
지금까지 아주 단순한 예시로 warm restart가 무엇인지 그리고 왜 필요한지에 대해서 알아보았다. warm restart에 대한 수식은 논문의 부록에서 찾아볼 수 있다.
Normalized weight decay
이전 포스트의 실험 3에서 Normalized weight decay이 등장하였다. 논문의 저자는 최적의 weight decay 상수 $\lambda$가 총 weight update 횟수에 종속적이라는 것을 실험을 통해 확인하였다. 아래 그림은 각각 CIFAR-10을 25번 학습하였을 때, 100번 학습하였을 때, 400번 학습하였을 때의 test error이다. 성능 상위 10개의 hyperparameter setting이 검은색 원으로 표시되어있다. epoch이 작을 수록 최적의 $\lambda$값은 크고, epoch이 클 수록 최적의 $\lambda$ 값이 작다는 것을 확인할 수 있다.
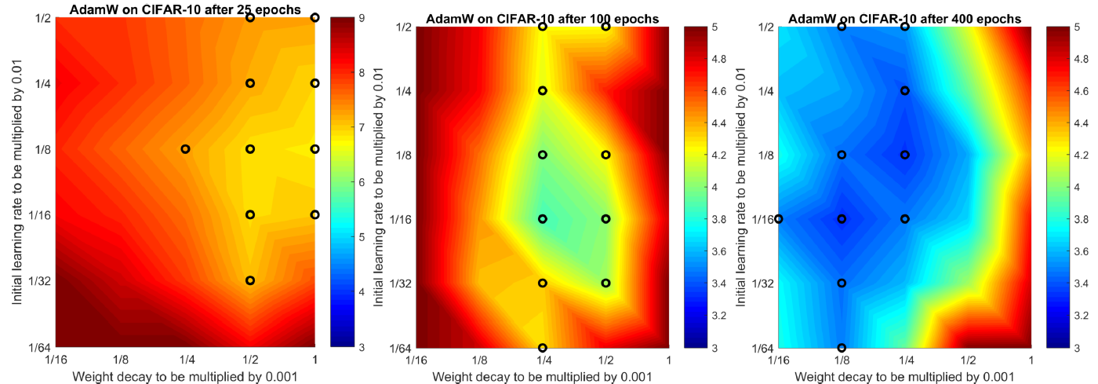
파라미터 업데이트 횟수에 따라 최적의 $\lambda$ 값이 달라진다면 하이퍼파라미터튜닝하기가 더 어려울 것이다. Normalized weight decay는 파라미터 업데이트 횟수에 따라 사용할 $\lambda$ 값을 정하는 방법이다. 사용자는 하이퍼파라미터로 $\lambda$ 대신 $\lambda_{norm}$이라는 것을 설정해준다. 다음으로 $\lambda = \lambda_{norm}\sqrt{\frac{b}{BT}}$ 으로 계산한 $\lambda$를 weight decay 상수값으로 사용하게 된다. 여기서 $b$는 batch size, $B$는 훈련 데이터 개수, $T$는 총 에폭 횟수다. 예를 들어,
배치 사이즈가 클수록, 데이터가 적을 수록, Epoch 수가 적을 수록 총 파라미터 업데이트 횟수는 적다.
- $b$ ↑, $B$ ↓, $T$ ↓ $\Longrightarrow$ $\sqrt{\frac{b}{BT}}$ ↑ $\Longrightarrow$ 큰 $\lambda$ 값 사용
배치 사이즈가 작을 수록, 데이터가 많을 수록, Epoch 수가 많을 수록 총 파라미터 업데이트 횟수는 많다.
- $b$ ↓, $B$ ↑, $T$ ↑ $\Longrightarrow$ $\sqrt{\frac{b}{BT}}$ ↓ $\Longrightarrow$ 작은 $\lambda$ 값 사용
사용자가 $\lambda_{norm}$만 설정해주면 총 파라미터 업데이트 횟수에 따라 사용할 $\lambda$ 값을 자동으로 선택해지기 때문에 Hyperparameter 튜닝하기가 한결 쉬워진다.
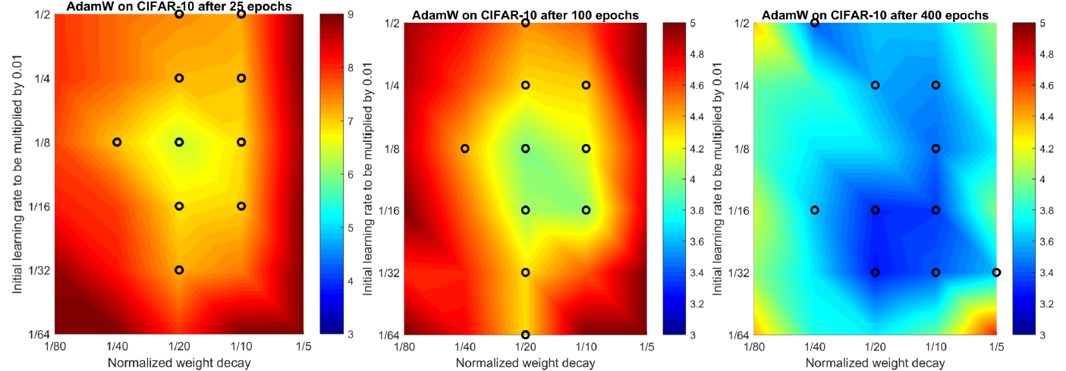
Normalized weight decay를 사용하는 경우 최적의 $\lambda_{norm}$값이 에폭에 따라 변하지 않는 것을 확인할 수 있다.
Experiment 4. AdamWR vs SGDWR vs AdamW vs SGDW vs Adam
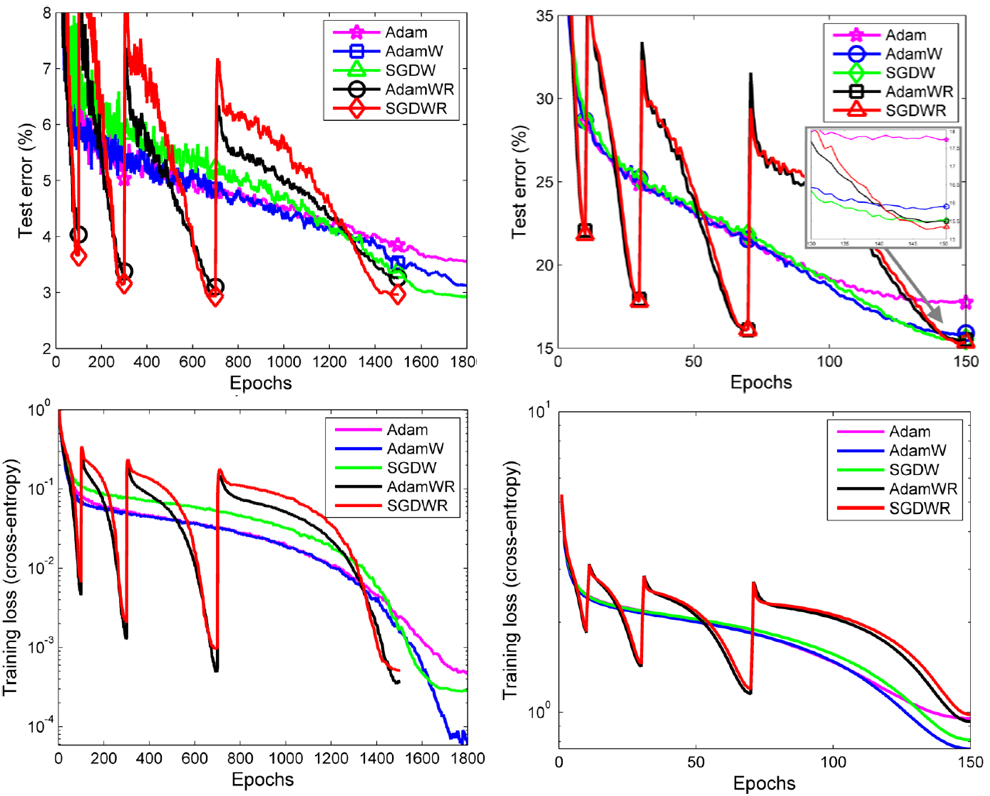
실험 환경
- 1열: Epoch에 따른 Top-1 test error and training loss on CIFAR-10
- 2열: Epoch에 따른 Top-5 test error and training loss on ImageNet32x32
- 어떤 모델을 사용했는지는 언급되지 않았지만 CIFAR-10에서 1,800 Epoch인걸보아 실험 3에서 사용한 26 2x96d ResNet일 것 같다.
결과 해석
- 이제는 warm restart의 learning curve가 왜 통통 튀는지 알 수 있다.
- 마지막 Epoch에서 학습을 마쳤을 때 AdamWR과 SGDWR의 training loss가 다른 알고리즘들에 비해 높지만 test error은 더 낮다. 즉, AdamWR과 SGDWR이 더 generalization을 잘한다는 것을 의미한다.
결론
1부와 2부를 요약하면 다음과 같다.
- Adaptive gradient methods 들은 L2 regularzation에 의한 weight decay 효과를 온전히 볼 수 없다.
- L2 regularziation에 의한 weight decay 효과와 별개로 weight decay를 weight 업데이트식에 넣어주었다.(decoupled weight decay)
- Learning rate schedule이 Adam의 성능 상승에 도움을 줄 수 있다는 것을 확인하였다.
- Warm restart까지 적용하면 밥도둑
References
[1] A Newbie’s Guide to Stochastic Gradient Descent With Restarts

