1. 서문

이번 포스트에서는 딥러닝에 사용되는 최적화알고리즘을 정리해보려고 한다.

• 지금까지 어떤 근거도 없이 Adam을 써왔는데, 최근에 잘 해결되지 않던 문제에 SGD를 써보니 성능이 훨씬 향상된 경험이 있다..
• 이에 “최적화 알고리즘을 알고 쓰자!”라는 마음이 생겼고, 그래서 이 포스트를 작성하게 되었다.
• 이 포스트는 최적화알고리즘 review 논문 [0] 을 재구성한 것을 미리 알린다.
• 또한 독자가 이미 기본적인 gradient descent 개념을 알고 있다고 생각하고 글을 작성하였다.

포스팅에서 다룰 내용들 : 글의 내용이 많기 때문에 궁금한 알고리즘만 골라서 보는 것을 추천합니다.

1. 서문
2. Gradient Descent
3. Challenges
4. Gradient Descent Optimization Algorithms
   • Momentum
   • Nesterov Accelerated Gradient
   • Adagrad
   • Adadelta
   • RMSprop
   • Adam
   • AdaMax
   • NAdam
5. 결론

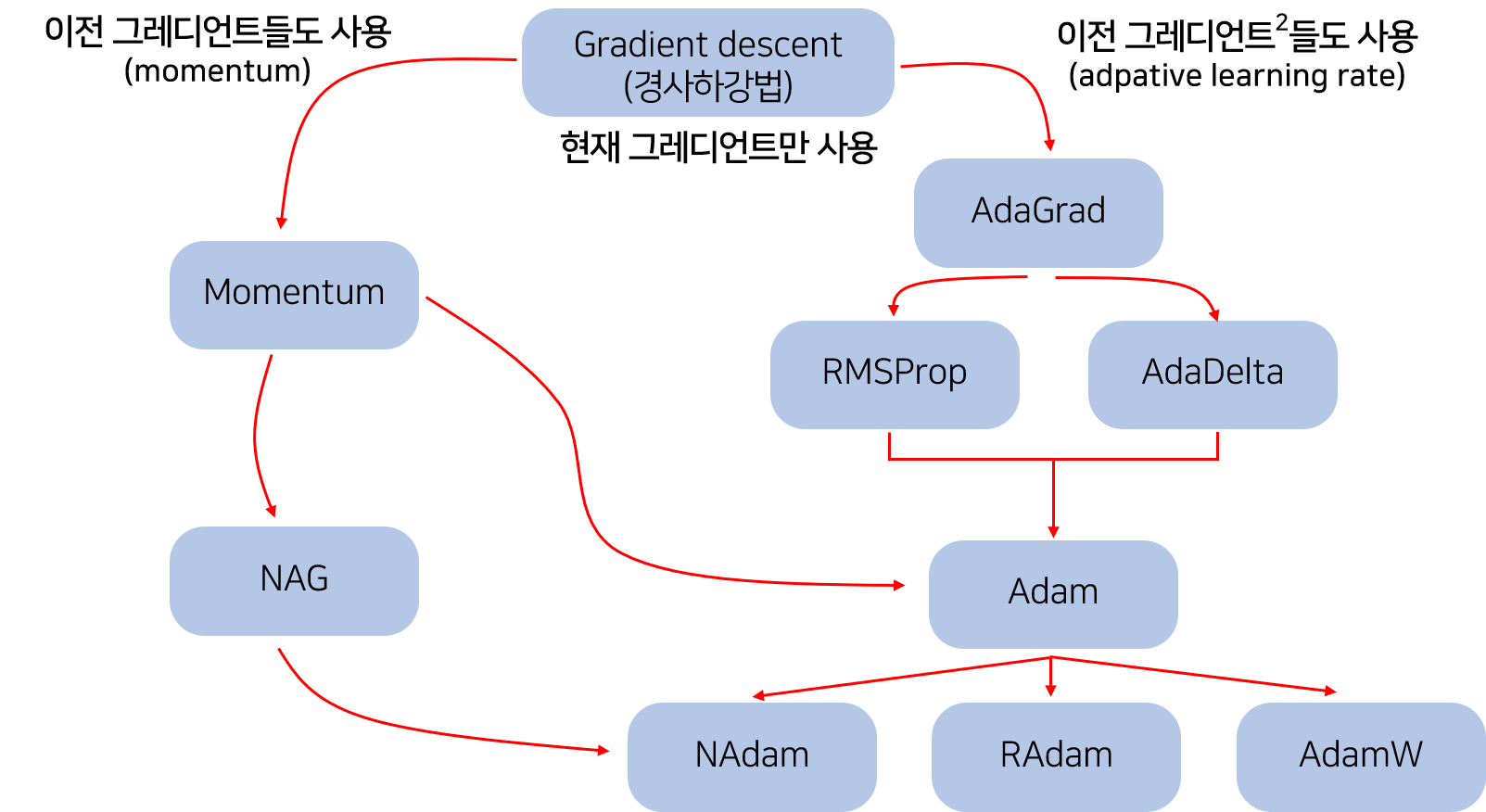
[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

2. Gradient Descent(경사하강법)

Gradient descent는 $\theta$를 미지수로 갖는 목적함수 $J(\theta)$를 최소화시키는 방법이다.

• 어떤 위치에 있는 $\theta$를 그 위치에서의 gradient인 $\nabla_{\theta}J(\theta)$의 반대 방향으로 이동시켜준다.
• 일반적인 gradient descent의 업데이트 식은 다음과 같다.
  
  $\theta_{t+1} = \theta_t - \eta\nabla_{\theta}J(\theta)$
  
  
• 여기서 $\eta$는 learning rate로 gradient 반대 방향으로 얼마나 업데이트할 것인지 결정한다.
  • 작은 $\eta$는 수렴 속도를 늦출 것이고, 큰 $\eta$는 minimum을 그냥 지나쳐버릴 수 있고 심하면 발산한다.
    
    

얼마나 많은 데이터를 목적함수의 gradient 계산에 사용할지에 따라 크게 세 가지의 gradient descent 종류가 있다.

Batch gradient descent

• ML/DL 에서 batch는 의외로 데이터 전체를 의미한다.
  • 이론보다 코딩을 먼저 경험했을 경우 batch_size = 32라는 인자를 많이 보기 때문에
  • batch가 데이터의 일부라고 알고 있을 수도 있다.
  • 몇몇 분들은 누가 그런 하찮은 생각을 한다고 의심할 수도 있겠지만,
  • 그게 나였다.
    
    
• 여러분이 알고있는 기본적인 gradient descent가 바로 batch gradient descent이다.
  • 손실함수는 보통 $J = \sum_{i=1}^{N}{error}$ 로 정의되는데
  • $\sum_{i=1}^{N}$ 이 데이터 N개 모두를 사용해서 손실함수를 만든다는 의미이다.
    
    
• 따라서, 한 번의 업데이트를 위해 모든 데이터가 계산에 포함되므로 속도가 느리다는 단점이 있다.
• batch gradient descent는 손실함수가 convex할 경우 global minimum 수렴을 보장하고, nonconvex일 경우에도 local minimum이 보장된다.
  
  

Stochastic gradient descent

• SGD는 한 번의 파라미터 업데이트를 위해 하나의 훈련 데이터를 사용한다.
  • 굳이 수식으로 적어보면 다음과 같다.
    
    $\theta_{t+1} = \theta_t - \eta\nabla_{\theta}J(\theta ; x^{(i)},y^{(i)})$
    
    
• 따라서 SGD는 batch gradient보다 훨씬 빠르게 업데이트가 진행되는 장점이 있다.
• 하지만 목적함수의 gradient가 하나의 데이터에 의해 결정되다보니
  • 매 업데이트마다 들쭉날쭉한 크기의 gradient로 파라미터를 업데이트하게 된다.
    • 이렇게 분산이 큰 gradient는 SGD가 local minimum에서 빠져나오게 만들 수도 있지만
    • 반대로 수렴을 방해할 수도 있다.
      
      

Mini-batch gradient descent

• Mini-batch gradient descent가 흔히 딥러닝을 사용할 때 쓰이는 방법이다.
  • 우리는 batch_size 인자를 넘겨 mini-batch 사이즈를 결정한다.
  • 그러면 최적화 알고리즘은 mini batch 사이즈의 데이터마다 손실함수를 만들고
  • gradient를 계산하여 파라미터를 업데이트한다.
• 당연히 batch GD보다 업데이트 속도가 빠르고, gradient의 크기도 들쭉날쭉하지 않다.

3. Challenges(문제점들)

vanilla gradient descent는 해결해야할 문제점들이 있다.

• 몇몇 뉴비들은 vanilla라는 단어를 처음 봤을 수도 있다.
  • 바닐라? 바나나인가? 싶을 것이다.
    • “이런 바보같은 생각을 누구해?” 싶겠지만
    • 사실 내가 그랬다. 내가 처음 vanilla를 봤을 때 바닐라맛 아이스크림 밖에 떠오르지 않았다.
  • vanilla는 그냥 “아주 기본적인”, “아무것도 건들이지 않은” 이런 느낌으로 사용되는 것 같다.
    
    

적절한 learning rate를 설정해주어야 한다.

• ML/DL을 하면서 learning rate가 꽤나 많이 중요하다는 것을 느낀다.

• 잘 만든 내 모델이 학습이 안 돼서 속상할 때, learning rate를 줄여주면 학습이 되는 경우도 많이 보았다.
  
  

• 수렴지점에서 더 정밀한 minimum을 찾기 위해서는 학습 중간에 learning rate를 조절해줘야한다.
  • SGD는 한 번 정해진 learning rate를 현재 학습 상황에 따라 바꿔주는 기능을 갖고 있지 않다.
  • 따라서, 우리가 learning rate의 리스트를 만들어서 특정 에포크마다 learning rate를 줄여주어야 한다.
    • 물론 실제 코딩에서는 decay를 사용하여 중간에 learning rate를 줄여줄 수 있다.
      
      

모든 파라미터에 대해 동일한 learning rate를 적용해준다.

• 각 파라미터의 중요도나 스케일 등이 모두 다를텐데, 모든 파라미터에 동일한 learning rate를 적용하는 것은 불합리해보인다.
• 앞으로 배울 방법들 중에 Ada가 들어가는 방법은 파라미터에 따라 learning rate를 자동으로 조절해주는 기능이 있다.
  • 물론 초기 learning rate를 설정해주어야 한다.
    
    

local minimum이나 saddle point에서 빠져나오기 힘들다.

• SGD가 높은 미끄럼틀에서 쭉 미끄러지다가 이제 막 평평한 밑면을 지나고 있다고 생각하자.
  • 우리는 SGD가 현재 파라미터 위치에서의 gradient 크기만큼 움직인다는 것을 알고 있다.
  • 밑면이 평평하다는 의미는 gradient가 0이라는 것이다.(극단적으로)
  • 따라서 파라미터는 평평한 밑면 도달하자마자 gradient가 0이 되어 멈추고 말 것이다.
• 이는 우리의 직관과 약간 다르다.
  • 우리는 미끄럼틀을 타고 내려올 때, 미끄럼틀 끝이 평평하다고 해서 바로 멈추지 않는다.
  • 내려오던 관성에 의해 다 내려온 뒤에도 몇 초간 더 이동할 것이다.
    
    

Vanilla gradient descent의 문제점을 몇 개 알아보았다.

• 이제부터 다양한 최적화 알고리즘들이 이 문제점들을 해결하는지에 대해 이야기해볼 것이다.
  
  

4. Gradient Descent Optimization Algorithms

여기서부터 본론이라고 말할 수 있다. 이 글을 찾아서 읽어볼 정도의 분들이라면 위 내용들은 이미 다 알고 있는 내용일 것이다.

• 사실 여기부터 다 작성하고 1,2,3을 작성한 것이기 때문에 이제부터 내용이 진짜 알차다.
• 1,2,3은 4를 다 쓰고나서 마지막에 초심 잃고 작성했기 때문에 내용이 많이 부실했다. 인정한다.
• 가보자.

Momentum

바로 앞에서 미끄럼틀을 내려오는 SGD 예시를 들어보았다. 그리고 우리의 직관에 대해서도 이야기해보았다. Momentum(관성) 방법은 우리의 직관을 그대로 반영한 최적화 방법이다. Momentum는 현재 파라미터를 업데이트해줄 때 이전 gradient들도 계산해 포함해주면서 이 문제를 해결한다.

• 즉, SGD가 미끄럼틀 끝에서 gradient가 0인 평평한 밑면을 만났다고 해도
• 미끄럼틀의 빗면의 gradient가 남아있어 SGD가 앞으로 쭉 갈 수 있게 만들어준다.
  
  

물론 이전에 있던 모든 gradient들을 있는 그대로 고려해준다면, 아주 긴 평평한 땅에서도 SGD는 절대 멈추지 않을 것이다.

• 그래서 Momentum은 이전 gradient들의 영향력을 매 업데이트마다 $\gamma$배 씩 감소시킨다.
  
  $v_t = \gamma v_{t-1} + \eta \nabla_{\theta_t}J(\theta_t)$
  $\theta_{t+1} = \theta_t - v_t$
  
  
• 점화식으로 표현되어있어서 감소한다는 것이 와닿지 않을 수도 있다.
  
  
  • $g_t = \eta\nabla_{\theta_t}(\theta_t)$ 그리고 $v_1 = g_1$ 이라고 하면
  • $v_2 = g_2 + \gamma g_1$
  • $v_3 = g_3 + \gamma g_2 + \gamma^2 g_1$
  • $v_4 = g_4 + \gamma g_3 + \gamma^2 g_2 + \gamma^3 g_1$
    
    
• $\gamma$는 보통 0과 1사이의 값이기 때문에 이런 식으로 점점 오래된 gradient의 영향력을 줄이며 모멘텀을 만든다. $\gamma$ 값은 주로 0.9를 사용한다.
  
  

Momentum의 힘 덕분에 이제 SGD는 관성을 사용해서 낮은 언덕정도는 탈출할 수 있게 되었다.

• 이는 SGD가 낮은 local minimum에서 벗어나 손실함수를 더 탐험할 수 있게 만들어준다.
  
  
  

Momentum 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

NAG(Nesterov accelerated gradient)

다시 미끄럼틀 위의 SGD를 상상해보자.

• 이제 우리의 SGD는 관성을 힘으로 미끄럼틀 끝에서도 더 나아갈 수 있게 되었다.
• 뿐만 아니라, 가파른 미끄럼틀에서 내려올 때면 관성이 그만큼 더 커지기 때문에 경로에 있는 작은 언덕 정도는 쑥 넘어버릴 수 있을 것이다.
  
  

관성에 재미를 붙인 SGD가 오늘도 미끄럼틀을 내려오고 있다.

• 앞에 평평한 땅이 있어도 SGD는 앞으로 나아갈 수 있다는 생각에 신이 나있다.
• 하지만 SGD가 밑면에 다다랐을 때쯤 앞에 압정이 있는 것을 발견했다.
• 엉덩이에 압정이 박히지 않으려면 SGD는 속도를 줄여야하지만 관성 때문에 SGD는 계속하여 앞으로 나아갔고,
• 결국 엉덩이에 압정이 박혀버렸다.
  
  

위의 끔찍한 예시에서 SGD는 앞에 압정이 있는 것을 알면서도 속도를 멈추지 못했다.

• NAG는 이런 문제를 해결하기 위해 나온 최적화 방법이다.
  • NAG는 앞을 미리 보고 현재의 관성을 조절하여 업데이트 크기를 바꾸는 방식으로 이 문제를 해결한다.
    
    
• Momentum 방법을 순서에 주의하여 다시 한 번 서술해보자.
  • Momentum은 먼저 현재 parameter 위치에서 gradient를 계산하고, → $\nabla_{\theta_t}J(\theta_t)$
  • 현재의 모먼트를 $v_t$ 구하여, → $v_t = \gamma v_{t-1} + \eta \nabla_{\theta_t}J(\theta_t)$
  • 모멘텀만큼 업데이트를 해주었다.→ $\theta_{t+1} = \theta_t - v_t$
    
    
• NAG도 순서에 주의하여 살펴보자.
  • NAG는 먼저 현재 parameter 위치로부터 현재 모멘텀 $v_t$만큼 떨어진 위치의 gradient를 계산한다. → $\nabla_{\theta_t}J(\theta_t -v_t)$
    • momentum 업데이트 식을 보면 $\theta_{t+1} = \theta_t - v_t$이므로 $\nabla_{\theta_{t}}J(\theta_{t+1})$ 계산하려는 시도인 것이다.
      • 즉, 미래를 보려고 노력하는 느낌이다.
    • 하지만 현재의 gradient를 구하기 전까지는 현재의 모멘텀을 알 수 없기 때문에 $\gamma v_{t-1}$을 $v_t$ 대신 사용해준다.
    • 즉, $\nabla_{\theta_t}J(\theta_t - \gamma v_{t-1})$를 식에 사용한다.
  • 다음으로 현재의 모멘텀을 계산해준다. → $v_t = \gamma v_{t-1} + \eta \nabla_{\theta_t}J(\theta_t - \gamma v_{t-1})$
  • 그리고 모멘텀만큼 업데이트를 해준다. → $\theta_{t+1} = \theta_t - v_t$
    
    
• 글이 길어졌지만, 다음과 같이 2줄의 식으로 요약할 수 있다.
  
  $v_t = \gamma v_{t-1} + \eta \nabla_{\theta_t}(\theta_t - \gamma v_{t-1})$
  $\theta_{t+1} = \theta_t - v_t$
  
  

NAG는 SGD가 관성에 의해 수렴 지점에서 요동치는 것을 방지해준다.

• RNN의 성능을 향상시켰다는 소문이 있다.

NAG 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

Adagrad

지금까지 SGD와 Momentum 그리고 NAG에 대해서 알아보았다.

• 이 세 가지 방법의 공통점 중 하나는 모든 파라미터에 대해서 같은 learning rate를 적용하여 업데이트를 한다는 점이다.
• 이것이 어떤 문제가 될까 싶겠지만, sparse한 데이터를 예시로 들어 알아보자.
  • $i$번 째 레이어의 인풋 노드 값을 차례대로 $a_1, a_2, \cdots, a_n $ 이라고 하자.
  • 이미 잘 알고 있는 것처럼 $i+1$번 째 레이어로 넘어가기 전에 파라미터들과 선형결합을 해준다.
    
    $w_0 + w_1a_1 + w_2a_2 + \cdots + w_na_n$
    
    
  • 이 때, 다른 얘들은 괜찮은데 유독 $a_2$ 는 sparse해서 주로 0값이 많이 나온다고 하자
    • 그러면 $a_2 = 0$일 때, $w_0 + w_1a_1 + 0 +w_3a_3 + \cdots + w_na_n$이 되고,
    • 손실함수에서도 $w_2$ term이 없어질 것이다.
    • $w_2$가 없는 손실함수를 $w_2$로 편미분한 값은 0이 나오고 $w_2$는 업데이트되지 않을 것이다.
  • 그렇게 $w_2$가 기억에서 사라질 때쯤 0 아닌 값을 갖는 $a_2$가 등장했다고 하자.
    • 아주 오랜만에 손실함수에는 $w_2$ term이 등장할 것이고 드디어 $w_2$를 업데이트할 수 있게 되었다.
  • 이 때 $w_2$는 그 동안 상대적으로 조금 업데이트됐기 때문에 수렴점까지 거리가 아직 많이 남은 상태이다.
    • 따라서 $w_2$는 다른 파라미터들보다 더 크게 업데이트를 해줘야만 수렴지점으로 조금이라도 빨리 갈 수 있을 것이다.
• 이런 이유로 각 파라미터의 업데이트 빈도 수에 따라 업데이트 크기를 다르게 해줘야 할 필요가 있다.
• 그리고 앞에서 다룬 세 가지 방법은 아쉽게도 이를 반영하지 못한다.
  
  

앞으로 다룰 방법들의 이름에는 Ada 라는 단어가 등장하는데 이는 Adaptive의 준말이다.

• ML이나 DL에서 Adaptive는 “상황에 맞게 변화하는” 이라는 맥락으로 사용되는 것 같다.
• 여담으로 Ada를 “아다”나 “에이다” 등으로 부르는 것보다 “어뎁티브”라고 부르는게 조금 더 있어 보인다.
  • 예를 들어, 아다그레드보다는 어뎁티브그레드 메서드라고 부르는게 더 있어 보인다.
    
    

Adagrad를 들어가기 전 서두가 다소 길었다. 이제 서두에서 제시한 문제를 Adagrad는 어떻게 해결하는지 알아보자.

• 파라미터마다 지금까지 얼마나 업데이트됐는지 알기 위해서 Adagrad는 parameter의 이전 gradient들을 저장한다.
  • $t$번 째 step의 $i$ 번 파라미터를 $\theta_{t,i}$
  • $t$ 시점에서 $\theta_{t,i}$에 대한 gradient 벡터를 $g_{t,i} = \nabla_{\theta_t}J(\theta_{t,i})$라 하자.
  • 이 새로운 노테이션으로 SGD의 업데이트 식을 다시 적어보면 다음과 같다.
    
    $\theta_{t+1, i} = \theta_{t,i} - \eta g_{t,i}$
    
    
• Adagrad는 다음과 같은 업데이트식을 사용한다.
  
  $\theta_{t+1, i} = \theta_{t,i} - \frac{\eta}{\sqrt{G_{t,ii} + \epsilon}}g_{t,i}$
  
  
  • $G_t$는 $i$번 째 대각원소로 $t$시점까지의 $\theta_i$에 대한 gradient들의 제곱의 총합을 갖는 대각행렬이다.
    • 즉, $G_{t,ii} = g_{1,i}^2+g_{2,i}^2+\cdots+g_{t,i}^2$ 이다.
  • 그리고 $\epsilon$은 분모가 0이 되는 것을 방지해주는 용도로 $10^{-8}$와 같이 아주 작은 값을 사용한다.
  • 신기한 것은, 분모에 루트를 씌어주지 않으면 알고리즘의 성능이 매우 구려진다고 한다.
• vectorize form으로 다시 써보면 다음과 같다.
  
  $\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{G_{t} + \epsilon}}\odot g_{t}$
  
  
  • $\odot$은 matrix vector 곱셈이다.
  • 그리고 분모에 어떻게 행렬이 들어가?라고 생각할 수 있는데
    • 대각행렬이기 때문에 성분들을 모두 역수 취하고 $\epsilon$ 더해주고 루트 씌워서 $\eta$를 곱한 새로운 행렬이라고 생각하자
• 업데이트 빈도 수가 높았던 파라미터는 분모에 의해 $\eta$보다 작게 업데이트되는 것을 알 수 있다.
  • $\eta$ 값은 주로 0.01을 사용한다고 한다.
• 하지만 Adagrad는 $t$가 증가하면서 $G_{t, ii}$ 값이 점점 커지게 되어 learning rate가 점점 소실되는 문제점이 있다.

Adagrad 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

Adadelta

해결하고자 한 문제점

1. Adagrad에서 발생한 iteration 마다 learning rate가 작아지는 문제
2. Hyperparameter인 learning rate($\eta$)의 필요
   
   

Adadelta는 $1$을 해결하기 위해 크기 $w$인 window를 사용한다.

• 즉, 지난 모든 gradient의 정보를 저장하는 것이 아니고 지난 $w$개의 gradient 정보만을 저장한다.

Adagrad와 또 다른 점은 gradient의 제곱의 합을 저장하지 않고, gradient의 제곱에 대한 기댓값을 저장한다는 것이다. → $E[g^2]_t$

또한 과거의 gradient 정보의 영향력을 감소시키기 위해 다음과 같은 식을 사용했다.

• 이를 decaying average of squared gradient 라고 표현한다.
  
  $E[g^2]_t = \gamma E[g^2] _{t-1} + (1-\gamma)g_t^2$
  
  
• 이 정보를 사용해서 $\Delta\theta_t$를 다음과 같이 결정한다.
  
  $\Delta\theta_t = -\frac{\eta}{\sqrt{E[g^2]_t + \epsilon}}g_t$
  
  
• $RMS$(root mean square)가 $\sqrt{\frac{x_1^2+x_2^2+\cdots+x_n^2}{n}}$ 이므로 다음처럼 더 간략히 표현할 수 있다.
  
  $\Delta\theta_t = -\frac{\eta}{RMS[g]_t}g_t$
  
  

논문의 저자는 first order method를 사용해서 parameter $\theta$를 업데이트할 경우 $\theta$와 $\Delta\theta$의 단위(unit)가 맞지 않다는 것에 주목했다.

• 예를 들어 미터($m$) 단위를 갖는 함수 $f$를 $m/s$ 단위인 $\nabla_t f$를 사용해서 업데이트하면 안 된다는 것이다.
  • 함수 f의 단위를 $unit(f)$, 정의역 $t$을 단위를 $unit(t)$라고 하면 first order method는
    
    $\frac{d}{dt} f(t)\Big|_{t=t_0} \approx \frac{f(t)-f(t_0)}{t-t_0}$
    
    
  • 이므로 단위는 $\frac{unit(f)}{unit(t)}$이 되고, 확장하여 $\frac{d^nf}{dt^n}$의 단위는 $\frac{unit(f)}{unit(t)^n}$ 이다.
  • 우리의 파라미터 업데이트 식 $\theta_t = \theta_{t-1} + \Delta\theta$ 에서 $\Delta\theta$ 는 $g = \nabla_{\theta_t} J(\theta_t)$ 를 포함하므로
    
    $\Delta\theta \propto g \propto \frac{\partial J}{\partial\theta} \propto \frac{1}{\text{unit of } \theta}$
    
    
  • 마치 $m$을 변화시키는데 $m/s$를 사용하는 것으로 볼 수 있다.(편의를 위해 $J$의 단위가 없다고 하자.)
    
    
• 따라서 $\Delta\theta = -\frac{\eta}{RMS[g]}g$에 second order method 행렬인 헤시안 행렬을 도입함으로써 unit을 맞춰줄 것이다.
  
  $\Delta\theta \propto H^{-1}g \propto \frac{\partial J/\partial\theta}{\partial^2 J/\partial\theta^2} \propto \text{unit of } \theta$
  
  
  • 여기서 $\frac{1}{\partial^2 J/\partial\theta^2} = - \frac{\Delta \theta}{\partial J/\partial\theta}$ 임을 이용했다.(Newton’s Method)
  • 우변의 분모에 해당하는 텀( $RMS[g]$ )은 가지고 있으므로 분자($\Delta\theta$) 텀을 만들기 위해 똑같이 다음을 생각한다.
    
    

  $E[\Delta\theta^2]_t = \gamma E[\Delta\theta^2] _{t-1} + (1-\gamma)\Delta\theta_t^2$
  
  

  • 다시 RMS를 사용해 간단히 적으면
    
    

  $\Delta\theta_t = -\frac{RMS[\Delta\theta]_t}{RMS[g]_t}g_t$
  
  

  • 이다. 하지만 현재($t$)는 업데이트 전이므로 $RMS[\Delta\theta]_t$ 값을 알 수 없기 때문에
  • 대신 $RMS[\Delta\theta] _{t-1}$ 을 근사값으로 사용한다.
    
    $\Delta\theta_t = -\frac{RMS[\Delta\theta] _{t-1}}{RMS[g] _t}g_t$
    
    
• 최종적으로 업데이트식은
  
  $\theta_{t+1} = \theta_t + \Delta\theta_t$
  
  

위의 단위를 맞춰주는 과정을 통해 우리는 더 이상 learning rate가 필요하지 않게 되었다.(문제 $2$ 해결)

Adadelta 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms
[1] 원논문 : ADADELTA: AN ADAPTIVE LEARNING RATE METHOD
[2] unit을 이해하게 된 StackOverFlow : what-are-the-units-of-the-second-derivative
[3] Root Mean Square
[4] 참고한 블로그글 : https://twinw.tistory.com/247 [흰고래의꿈]
[5] 참고한 블로그글 : http://incredible.ai/artificial-intelligence/2017/04/10/Optimizer-Adadelta/

RMSprop

해결하고자 한 문제점

• Adagrad의 learning rate 가 작아지는 문제(Adadelta와 마찬가지)
  
  

사실, Adadelta에서 이야기했던 첫 번 째 업데이트식과 같다.

$E[g^2] _t = 0.9 E[g^2] _{t-1} + 0.1g _t^2$

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2] + \epsilon}}g_t$

• Adadelta와 비슷한 시기에 Geof Hinton이 그의 코세라 강의에서 제안한 방법
• 적절한 $\gamma$ 값으로 0.9를, $\eta$ 값으로 0.001을 제안
  
  

RMSProp 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

Adam(Adaptive Moment Estimation)

Adam은 Adagrad, Adadelta, RMSprop 처럼 각 파라미터마다 다른 크기의 업데이트를 적용하는 방법이다.

특히 Adadelta 에서 사용한 decaying average of squared gradients 뿐만 아니라. decaying average of gradients를 사용한다.

• 즉, Adadelta에서 $E[g^2]_t$ 를 업데이트에 사용한 것처럼, Adam은 $E[g]_t$ 도 업데이트에 사용한다.
  • 이 맥락에서 Adam의 Full name에 있는 moment의 정체를 알 수 있다.
    • 이전 언급한 momentum method의 momentum는 “관성” 같은 느낌이지만
    • Adam의 moment는 통계에서 등장하는 용어이다.
      • 일반적으로 확률변수 $X$의 $n$차 moment를 $E[X^n]$으로 정의한다.
      • 1차 moment $E[X]$는 모평균이고
      • 2차 moment $E[X^2]$와 1차 moment를 사용해서 모분산을 얻을 수 있다.
      • 물론, $E[X]$와 $E[X^2]$ 은 모수이기 때문에 알 수 없는 값이다.
      • 따라서 표본평균과 표본제곱의평균으로 1,2차 moment를 추정해야한다.
  • 그래서 추정(estimation)이 들어가 Adaptive Moment Estimation인 것이다.
    
    
• $m_t$를 gradient의 1차 moment에 대한 추정치, $v_t$를 2차 moment에 대한 추정치라 하자.
• 그리고 이제는 익숙한 가중평균식을 도입하면 다음과 같다.
  
  $m_t = \beta_1m_{t-1} + (1-\beta_1)g_t$
  $v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2$
  
  
• $m_t$와 $v_t$의 초기값을 0벡터로 주면, 학습 초기에 가중치들이 0으로 편향되는 경향이 있다.
  • 특히 decay rate 가 작으면, 즉 $\beta_1$과 $\beta_2$가 1에 가까우면 편향이 더 심해진다.
  • 편향을 잡아주기 위해 다음과 같이 bias-corrected를 계산한다.
    
    $\hat{m_t} = \frac{m_t}{1-\beta_1^t}$
    $\hat{v_t} = \frac{v_t}{1-\beta_2^t}$
    
    
• 최종적으로 업데이트 식은 다음과 같다.
  
  $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t}$
  
  • 저자는 $\beta_1=0.9$, $\beta_2=0,999$, $\epsilon=10^{-8}$을 default 값으로 설정하였다.

Adam 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

AdaMax

요약하자면 AdaMax는 Adam의 $v_t$ 텀에 다른 norm을 사용한 방법이다.

• Adam의 $v_t$ term과 최종 업데이트식 다음과 같다.
  
  $v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2$
  $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t}$
  
  
• 현재 gradient g_t에 제곱이 있고, 최종 업데이트식에는 루트가 있다.
  • 즉, 현재 gradient의 $l_2$ norm을 사용했다.
• 따라서 Adam의 $l_2$ norm을 $l_p$ norm으로 일반화한 방법을 생각할 수 있다.
  
  $v_t = \beta_2^pv_{t-1} + (1-\beta_2^p)|g_t|^p$
  
  
  • 여기서 $\beta_2^p$는 $\beta_2$의 $p$ 제곱이 아니고 그냥 계수의 노테이션이다.
• $l_p$ norm 값은 $p$이 커질수록 불안정(numerically unstable)해진다.
• 하지만 $l_\infty$ norm은 일반적으로 안정적인 양상을 보인다.
• 이런 이유로 AdaMax는 $v_t$에 $l_\infty$을 사용했고, stable한 값에 수렴한다는 것을 보였다.
• Adam의 노테이션과 구분짓기 위하여 $u_t$를 사용해서 표현하면 다음과 같다.
  
  $u_t = \beta_2^{\infty}v_{t-1} + (1-\beta_2^{\infty})| g_t |^{\infty}$
  $u_t = max(\beta_2v_{t-1}, | g_t |)$
  
  
• 최종 업데이트식은 다음과 같다.
  
  $\theta_{t+1} = \theta_t - \frac{\eta}{u_t}\hat{m_t}$
  
  
  • Adam과 다르게 max operation은 0으로의 편향이 없기 때문에 편향 보정을 해줄 필요가 없다.
  • 적절한 초기값은 $\eta = 0.002$, $\beta_1=0.9$, $\beta_2=0,999$ 이다.

AdaMax 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

NAdam(Nesterov-accelerated Adaptive Memoment Adam)

NAdam은 이름에서 알 수 있는 것처럼 NAG와 Adam을 섞은 방법이다.

Momentum과 NAG(Nesterov accelarated gradient)를 다시 한 번 보고가자.

• 순서에 주의해서 Momentum 방법 먼저 살펴보자
  • 현재 gradient $\nabla_{\theta_t}J(\theta_t)$를 구하고
  • 구한 gradient에 이전 step의 moment에 $\gamma$를 곱해준 $\gamma m_{t-1}$을 더하여 현재 moment $m_t$를 산출해서
  • 최종 업데이트($\theta_{t+1}$)에 사용한다.
  • 이를 식으로 보면 다음과 같다.
    
    $g_t = \nabla_{\theta_t}J(\theta_t)$
    $m_t = \gamma m_{t-1} + \eta g_t$
    $\theta_{t+1} = \theta_t - m_t$
    $\therefore \theta_{t+1} = \theta_t - (\gamma m_{t-1} + \eta g_t)$
    
    
• NAG 또한 순서에 주의하며 복습해보자.
  • 현재의 위치 $\theta_t$에서 현재의 moment $m_t$만큼 움직인 자리의 gradient $\nabla_{\theta_t}J(\theta_t - m_t)$를 구하고,
    • 아쉽게도 $m_t$ 값을 모르기 때문에 $\gamma m_{t-1}$을 $m_t$ 대신 사용한다.
  • 구한 gradient에 이전 step의 moment에 $\gamma$를 곱해준 $\gamma m_{t-1}$을 더하여 현재 moment $m_t$를 산출해서
  • 최종 업데이트($\theta_{t+1}$)에 사용한다.
  • 이를 식으로 보면 다음과 같다.
    
    $g_t = \nabla_{\theta_t}J(\theta_t - \gamma m_{t-1})$
    $m_t = \gamma m_{t-1} + \eta g_t$
    $\theta_{t+1} = \theta_t - m_t$
    $\therefore \theta_{t+1} = \theta_t - (\gamma m_{t-1} + \eta g_t)$
    
    

이제 다시 NAdam으로 돌아가자.

• NAdam은 NAV를 조금 변형했다.
  • $m_{t-1}$을 gradient를 업데이트할 때와, $\theta$를 업데이트할 때 2번 사용하였다.
  • NAdam은 이렇게 momentum을 2번 적용하는 대신 업데이트할 때만 적용할 것과
  • $m_{t-1}$ 대신 $m_t$를 사용하는 것을 제안하였다. 즉,
    
    $g_t = \nabla_{\theta_t}J(\theta_t)$
    $m_t = \gamma m_{t-1} + \eta g_t$
    $\theta_{t+1} = \theta_t - (\gamma m_{t} + \eta g_t)$
    $\therefore \theta_{t+1} = \theta_t - m_{t+1}$
    
    
    • 위에서 본 식들과 3,4번 째 식의 순서가 다름에 주의하자.
    • 업데이트 식에서 $\gamma m_{t-1}$ 대신 $\gamma m_{t}$를 사용함으로써
    • 마치 $m_{t+1}$을 사용하여 미래의 momentum을 사용한 효과를 가졌다.
  • 이제 변형된 NAV와 Adam을 합쳐보자. 먼저, Adam의 업데이트식은 다음과 같다.
    
    $m_t = \beta_1m_{t-1} + (1-\beta_1)g_t$
    $\hat{m_t} = \frac{m_t}{1-\beta_1^t}$
    $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t}$
    
    
  • 1,2번 식을 3번 식에 대입하면
    
    $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}(\frac{\beta_1 m_{t-1}}{1-\beta_1^t} + \frac{(1-\beta_1)g_t}{1-\beta_1^t})$
    $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}(\beta_1\hat{m}_{t-1} + \frac{(1-\beta_1)g_t}{1-\beta_1^t})$
    
    
  • 으로 정리할 수 있고, 마지막으로 변형된 NAV처럼 $m_{t-1}$ 대신 $m_t$를 사용해주자
    
    $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}(\beta_1\hat{m}_{t} + \frac{(1-\beta_1)g_t}{1-\beta_1^t})$
    
    

NAdam 참고문헌

[0] Optimizer overview 논문 : An overview of gradient descent optimization algorithms

결론

SGD부터 NAdam까지 모든 알고리즘을 살펴보았다. 각 알고리즘들은 이전 알고리즘들의 한계점을 보완해가며 발전해갔다.

• 먼저 SGD는 업데이트 한 번에 데이터 하나를 사용하여 Batch GD의 시간 문제를 해결했고,
• Momentum은 SGD의 작은 gradient 때문에 작은 언덕이나 saddle point를 빠져나가지 못하는 것을 momentum을 도입하여 해결했다.
• NAG는 다음 step의 gradient를 먼저 살펴보고 Momentum을 조절하여 minimum에 안정적으로 들어갈 수 있게 했으며,
• Adagrad는 업데이트 빈도가 다른 파라미터에 대해서도 같은 비율로 업데이트하는 것을 이전 gradient들의 합을 기억함으로써 문제를 해결하였다.
• RMSProp과 Adadelta는 Adagrad의 learning rate가 점점 소실되는 것을 gradient의 2차 모먼트를 통해 보완했고,
• Adam은 RMSProp에 1차 모먼트를 도입하여 RMSProp과 Momentum을 합친 효과를 볼 수 있었다.
• AdaMax는 Adam의 2차 모먼트에 있는 gradient의 norm을 max norm으로 바꿔주었고
• 마지막으로 NAdam은 ADAM에 NAG를 더해주어서 momentum을 보완해주었다.