빠른 텐서 연산을 위한 자료구조
오늘은 Deep learning with Pytorch이란 책을 읽으면서 좋았던 내용을 공유하는 포스팅을 작성하고자 한다. 다른 딥러닝 책들과는 다르게 텐서에 대해서 너무 얕지도 않게 너무 깊지도 않게 설명해주고 있어서 좋았다. 이 포스팅에서는 텐서 연산을 빠르게 수행하기 위하여 PyTorch에서는 텐서를 어떻게 메모리에 저장하는지에 이야기할 것이다.
들어가기 전에
- 참고한 책 Deep learning with Pytorch는 아직 출판되지 않았지만 첨부한 링크에서 책의 6장까지 무료로 읽어볼 수 있다. (성공하면 꼭 사서 읽어봐야지)
- 아직 읽어보지 않았지만 PyTorch의 핵심인
autograd를 설명하는 챕터도 따로 있다. - 일부 그림들은 책에 있는 그림들을 참고하여 내가 PPT로 만든 것이다.
- 저작권 문제가 있는건 아니겠지 …
이 포스트에서 다룰 내용들
텐서(Tensor)란 무엇인가?
우리는 $\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix}$ 을 벡터라고 부른다. 그리고 벡터들을 나란히 모아놓은 $\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1d} \\ a_{21} & a_{22} & \cdots & a_{2d} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nd} \end{bmatrix}$ 을 행렬이라고 부른다. 그리고 이들 행렬을 쌓아올린 직육면체 형태의 자료구조도 생각해볼 수 있다. 그리고 상상은 할 수 없겠지만 직육면체들을 쌓아올린 4차원 형태의 자료구조도 분명히 있을 것이다. 텐서는 이러한 자료구조들을 일반적으로 가리키는 단어이다. 벡터는 1차원 텐서, 행렬은 2차원 텐서, 직육면체 형태의 자료구조는 3차원 텐서이다. 텐서를 numpy스럽게 말하면 다차원 배열(multidimensional array)이라고 부를 수 있다. 아래 그림처럼 $N$차원 텐서에 저장되어 있는 값에 접근하기 위해서는 $N$개의 인덱스가 필요하다.

우리는 Python에서 list를 사용해서 텐서를 쉽게 만들 수 있다. list에 값을 순서대로 넣으면 1차원 텐서를 만들 수 있고, list에 또 다른 list들을 차례대로 넣으면 2차원 텐서(list of list)를 만들 수 있다, 마찬가지로 list에 list of list들을 순서대로 넣으면 3차원 텐서를 만들 수 있을 것이다. 하지만 우리는 텐서를 다룰 때 파이썬 list of list를 사용하지 않고 NumPy, PyTorch, TensorFlow 등과 같은 라이브러리들을 사용한다. 이들 라이브러리들과 파이썬 list는 텐서를 다룰 때 어떠한 차이가 있는 것이 분명하다. 다음 장에서는 python list이 왜 텐서를 다루는데 비효율적인지 알아보자
파이썬 list가 텐서를 다루는데 비효율적인 이유
나는 컴퓨터 과학에 대해서는 아는 것이 없기 때문에, 파이썬 list가 텐서를 다루는데 비효율적인 이유를 책에서 설명하고 있는 정도만 나열하고자 한다.
1. Numbers in Python are full-fledged objects.
마땅히 의역할 수 있는 적절한 문장이 없어서 그대로 가져왔다. C언어에서 int나 float 자료형에 4바이트를 할당하는 것과 다르게 파이썬에서는 최소 8바이트를 할당한다. 최소인 이유는 파이썬에서는 숫자의 길이에 따라 8바이트보다 더 많은 메모리를 할당하기 때문이다. 예를 들어, C언어에서는 123와 같은 작은 숫자를 담는 변수를 선언할 때, 평범하게 int를 사용해서 4바이트를 할당하거나 또는 short를 사용해서 2바이트만 할당할 수 있다. 하지만 파이썬에서는 8바이트를 할당하는 double을 사용하는 셈이다. 요새 언어로 파이썬은 “메모리를 Flex해버렸지 뭐야”라고 할 수 있다. 데이터의 개수가 적다면 숫자들 각각에 8바이트를 할당하는 것이 별로 큰 문제가 되지 않겠지만, 몇 백 만개의 데이터를 분석해야 하는 상황에서는 8바이트를 할당하는 것은 굉장히 비효율적일 것이다.
밑의 코드는 위의 내용에 대한 내가 진행한 팩트 체크이다. sys의 getsizeof는 할당된 메모리의 바이트를 반환해주는 함수이다.
a = 1.0
print("Size of a in bytes: ", getsizeof(a))
Size of a in bytes: 24
위에서 8바이트라고 했는데 getsizeof의 출력값은 24바이트이다. 파이썬은 C와는 다르게 object를 메모리에 저장할 때 추가 정보 overhead를 저장한다. 24바이트 중 8바이트에는 reference counter가 저장되고, 8바이트는 float class를 가리키는데 사용되고 나머지 8바이트가 숫자를 나타내는데 사용된다. reference counter는 메모리를 효율적으로 관리하는 방법이라고 한다. [2]
2. 파이썬 list는 object들의 순차적으로 모아둔 것 뿐이다.
- 파이썬 리스트는 그저 원소들을 가리키는 포인터들을 모아놓은 집합이기 때문에 원소들을 메모리 상에 최적화하여 저장하는 방법이 따로 없다.
- 파이썬은 리스트와 리스트의 덧셈이나 내적 등의 리스트 사이의 연산을 지원하지 않는다.
- list는 결국 1차원이다. list of list를 사용할 수 있으나 이는 비효율적이다.
3. Python 느리다.
어우 컴파일 이야기까지 나와서 생략. 아무튼 파이썬은 느리기 때문에 대규모 수학연산을 빠르게 수행하기 위해서는 C언어와 같은 low level 언어를 사용해서 효율적인 코딩을 해야한다.
이러한 이유로 텐서를 다루는데 파이썬은 적합하지 않다. 다행히도 NumPy나 PyTorch같은 라이브러리들은 메모리상에서 텐서를 효율적으로 다룰 수 있는 자료구조를 사용한다. 뿐만 아니라 low-level implementation으로 효율적인 텐서 연산을 제공한다. 다음 장에서는 NumPy나 PyTorch이 어떤 자료구조를 사용해서 텐서를 다루는지 알아볼 것이다.
효율적으로 텐서를 다루는 방법 - 메모리
PyTorch의 텐서나 NumPy의 다차원 배열은 파이썬 list와 다른 방법으로 메모리를 할당한다. 파이썬의 list에 있는 원소들은 메모리의 이곳저곳에 따로따로 저장되어 있다. 반면, PyTorch의 텐서나 NumPy의 다차원 배열의 원소들은 C언어의 자료형을 갖으며 메모리 상에서 인접한 곳에 블럭 형태로 저장된다. 아래 그림을 보면 조금 이해가 편할 것이다.
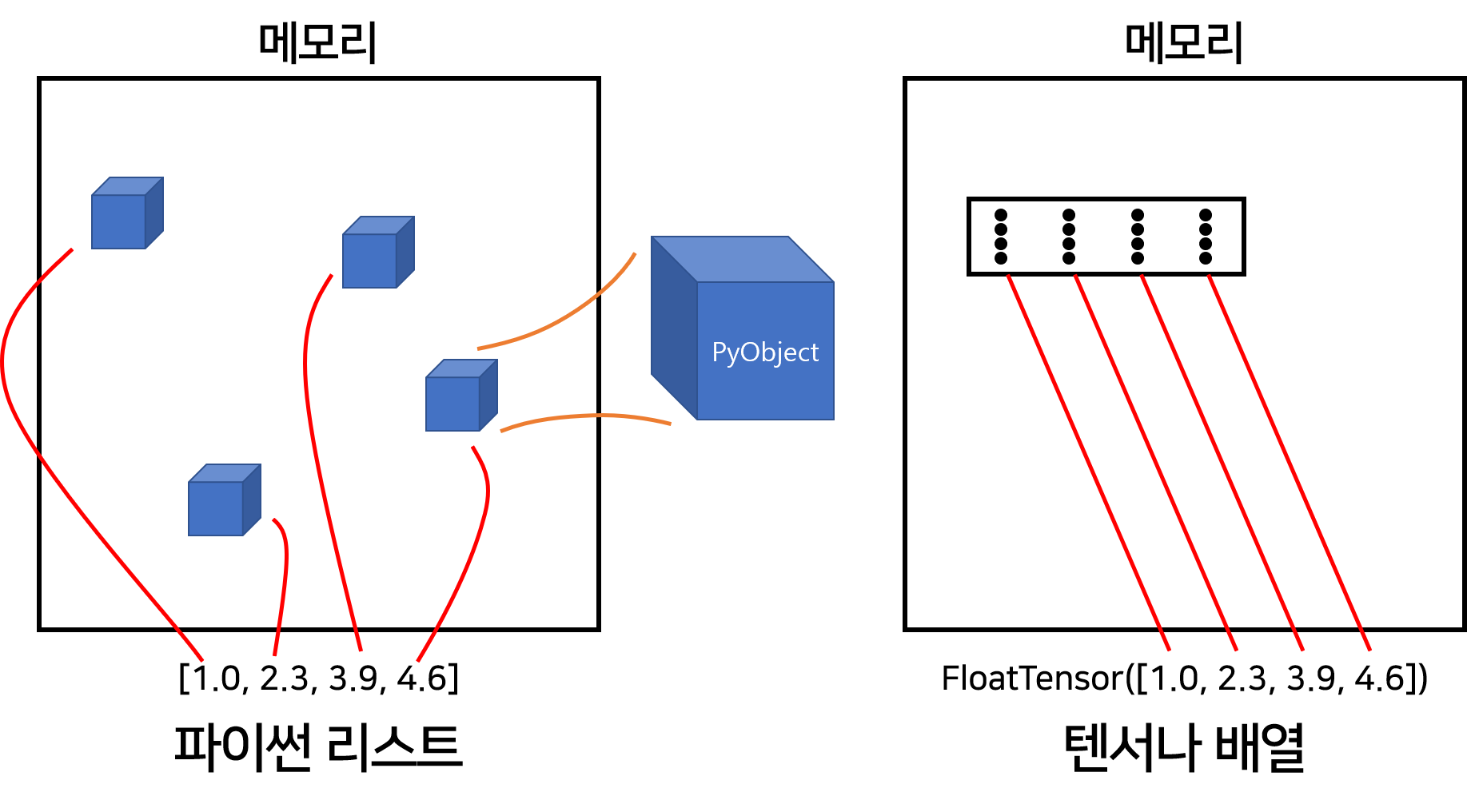
위 그림이 결코 뇌피셜이 아니라는 것을 다음 코드를 통해 팩트 체크할 수 있다. id는 파이썬 기본 내장함수로서 메모리 주소값을 반환해준다. 우선 세 개의 값 1.0, 2.0, 3.0을 각각 변수 a0, a1, a2에 넣고 주소를 출력해보자.
a0 = 1.0
a1 = 2.0
a2 = 3.0
print(id(a0) , id(a1), id(a2))
1447428604072 1447428603952 1447428604264
a0, a1, a2를 원소로 갖는 파이썬 list a를 정의하고 a의 각 원소의 주소를 출력해보자.
a = [a0, a1, a2]
print(id(a[0]) , id(a[1]), id(a[2]))
1447428604072 1447428603952 1447428604264
a의 원소들의 주소는 각각 a0, a1, a2의 주소와 같은 것을 확인할 수 있다. 마찬가지로 a0, a1, a2를 원소로 갖는 PyTorch 텐서 b를 만들고 각 원소들의 주소를 출력해보자
b = torch.tensor([a0, a1, a2])
print(id(b[0]), id(b[1]), id(b[2]))
1447428866624 1447428866624 1447428866624
a0, a1, a2의 주소가 아니며 게다가 같은 주소를 가리키고 있는 것을 확인할 수 있다.
뿐만 아니라 파이썬이 숫자에 full-fledged 하게 메모리를 할당하는 것과 다르게 PyTorch에서는 다양한 숫자 자료형을 제공함으로써 효율적으로 메모리를 관리할 수 있는 기회를 준다. PyTorch에서 제공하는 자료형은 다음과 같다.
- torch.float32 (torch.float): 32비트 floating-point
- torch.float64 (torch.double): 64비트 floating-point
- torch.float16 (torch.half): 16비트 floating-point
- torch.int8: 부포를 포함하는 8비트 정수
- torch.uint8: 부호를 포함하지 않는 8비트 정수
- torch.int16 (torch.short): 부호를 포함하는 16비트 정수
- torch.int32 (torch.int): 부호를 포함하는 32비트 정수
- torch.int64 (torch.long): 부호를 포함하는 64비트 정수
메모리 관련하여 한 가지의 코드 예시를 더 살펴보자
data = [[1.0, 2.0],
[3.0, 4.0],
[5.0, 6.0]]
a = torch.tensor(data)
print(a)
tensor([[1., 2.],
[3., 4.],
[5., 6.]])
b = a[1,:]
print(b)
tensor([3., 4.])
텐서 a의 두 번째 행만 인덱싱한 텐서 b는 새로운 메모리에 복사되어 저장될까? 그렇지 않다. 인덱싱할 때마다 새로운 메모리를 할당하는 것은 굉장히 비효율적이다. 예를 들어, 텐서 a에 수 천 만개의 데이터 저장되어 있고 이것의 일부를 인덱싱한 텐서 b는 수 백 만개의 데이터를 포함하고 있다면 b에 새로운 메모리를 할당하는 것은 굉장히 비효율적일 것이기 때문이다. b에 새로운 메모리를 할당하는 대신 텐서 a를 다르게 바라보는 관점을 반환받게 된다. 이 사실은 b의 원소를 바꾸면 a의 원소도 바뀌는 것을 통해 확인할 수 있다.
b[0] = -999
print(b)
print(a)
tensor([-999., 4.])
tensor([[ 1., 2.],
[-999., 4.],
[ 5., 6.]])
효율적으로 텐서를 다루는 방법 - 자료구조
우리의 생각과는 다르게 1차원 텐서이든, 2차원 텐서이든 혹은 $d$차원 텐서이든 메모리 안에는 1차원 배열의 형태로 저장된다. 텐서를 효율적으로 다룰 수 있도록 만들어주는 이 1차원 배열은 storage라고 부른다. storage는 offset 과 stride 라는 개념을 사용하여 사용자가 인덱싱한 텐서의 값에 접근한다. offset 과 stride 는 잠시 후에 자세히 알아보자
다차원 텐서를 1차원 storage를 다루기 때문에 서로 다른 두 텐서가 같은 모습을 storage를 만들 수 있다. 하지만 두 storage의 offset과 stride가 서로 다를 것이다. 다음 그림을 통해 이해해보자.
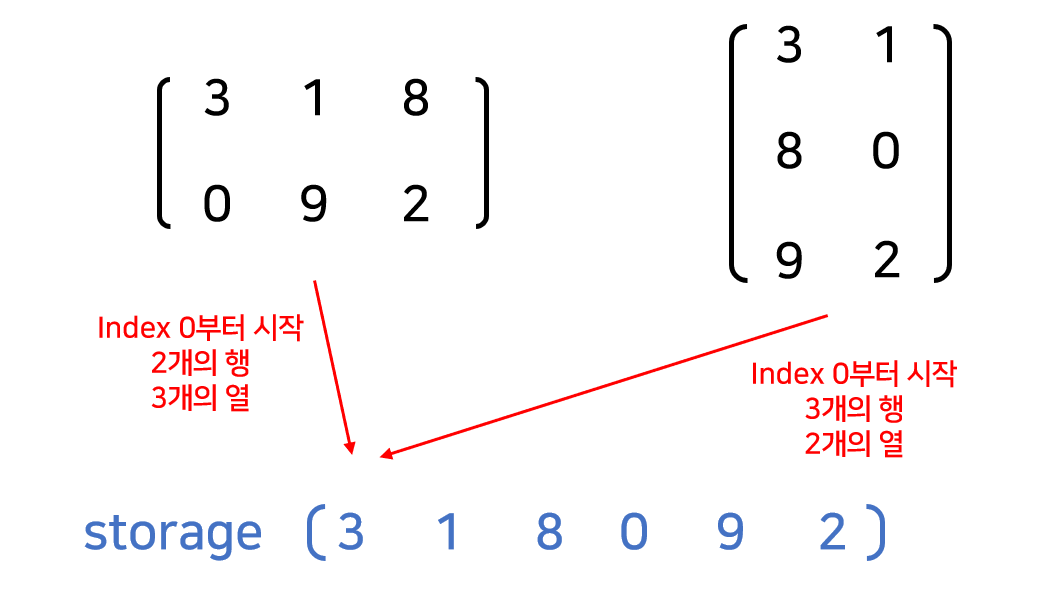
그림의 두 텐서는 분명히 다르지만 이들의 storage는 서로 같다. 그럼 storage만 보고는 이 둘을 구분지을 수 없을 것이다. 빨간색으로 나타낸 정보가 두 텐서를 구분지을 수 있을 것이다.
offset 은 텐서의 첫 번째 원소가 storage에 저장되어 있는 인덱스이다. 그림의 양쪽 텐서의 첫 번째 원소 3은 storage의 0번 째 인덱스에 저장되어 있다. 따라서 양쪽 텐서의 storage의 offset은 0이 된다.
stride 는 텐서 안의 어떤 한 값에서 다음 원소를 얻기 위하여 storage에서 뛰어넘어야할 인덱스의 개수이다. 이 때 어떤 원소의 다음 원소는 행방향과 열방향으로 있을 수 있다. 따라서 storage의 stride는 텐서의 차원만큼 정의할 수 있다.
예를 들어, 그림의 왼쪽 텐서에서 3의 다음 원소는 행방향으로는 0, 열방향으로는 1이다. storage에서 0을 얻기 위해서는 3에서 3칸을 뛰어넘어야하고, 1을 얻기 위해서는 1을 뛰어넘어야한다. 따라서 왼쪽 텐서의 storage의 stride는 (3,1)이다.
반대로, 오른쪽 텐서에서 8의 다음 원소는 행방향으로는 0, 열방향으로는 1이다. storage에서 8을 얻기 위해서는 3에서 2칸을 뛰어넘어야하고, 1을 얻기 위해서는 1을 뛰어넘어야한다. 따라서 왼쪽 텐서의 storage의 stride는 (2,1)이다.
지금까지 알아본 내용을 코드를 통해 확인해보자
a = torch.tensor([[3,1,8],
[0,9,2]])
print("============storage==========")
print(a.storage())
print("=============================")
print("Offset: ", a.storage_offset())
print("Strides: ", a.stride())
============storage==========
3
1
8
0
9
2
[torch.LongStorage of size 6]
=============================
Offset: 0
Strides: (3, 1)
b = torch.tensor([[3,1],
[8,0],
[9,2]])
print("============storage==========")
print(b.storage())
print("=============================")
print("Offset: ", b.storage_offset())
print("Strides: ", b.stride())
============storage==========
3
1
8
0
9
2
[torch.LongStorage of size 6]
=============================
Offset: 0
Strides: (2, 1)
다음과 같은 한 가지 예시를 더 살펴보자.
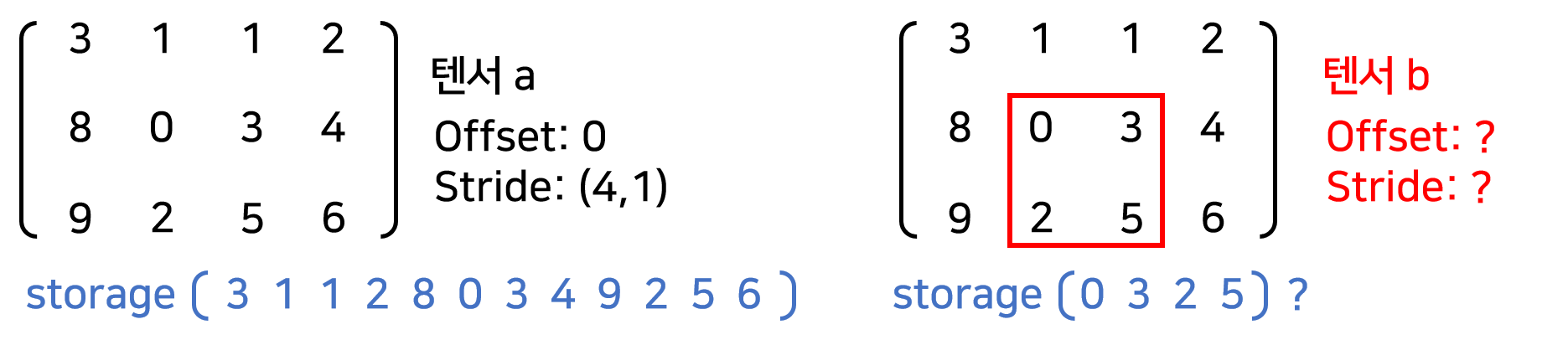
a = torch.tensor([[3,1,1,2],
[8,0,3,4],
[9,2,5,6]])
print("============storage==========")
print(a.storage())
print("=============================")
print("Offset: ", a.storage_offset())
print("Strides: ", a.stride())
============storage==========
3
1
1
2
8
0
3
4
9
2
5
6
[torch.LongStorage of size 12]
=============================
Offset: 0
Strides: (4, 1)
b = a[1:3,1:3]
print("============storage==========")
print(b.storage())
print("=============================")
print("Offset: ", b.storage_offset())
print("Strides: ", b.stride())
============storage==========
3
1
1
2
8
0
3
4
9
2
5
6
[torch.LongStorage of size 12]
=============================
Offset: 5
Strides: (4, 1)
b는 a를 인덱싱하여 얻은 $2\times2$ 텐서이다. 그런데 우리의 기대와는 다르게 storage가 [0,3,2,4]가 아니고 텐서 a의 storage와 같다. 그리고 offset은 5이다. b의 첫 번째 원소 0이 storage의 인덱스 5에 저장되어 있기 때문이다. strides는 마찬가지로 (4,1)이다. 곰곰이 생각해보면 여기에 텐서 b의 size 정보까지 합쳐서 a와 b를 구분지을 수 있다는 것을 알 수 있다. 이것이 메모리편에서 말했던 텐서 b 대신 “텐서 a를 다르게 바라보는 관점을 반환받게 된다.”라는 것을 보여준다. 실제로 a와 b의 storage는 같은 주소를 갖는다.
print(id(a.storage()), id(b.storage()))
1447428900552 1447428900552
몇 차원의 텐서가 주어지든 1차원 배열 storage와 offset 그리고 strides 정보만 알면 텐서 안의 모든 값에 효율적으로 접근할 수 있다. 예를 들어, 2차원 텐서의 (i, j) 원소는 storage에서 $\text{storage_offset + stirde[0] * i + stirde[1] * j}$ 인덱스에 위치해있다.
1차원 배열 storage을 이용하면 텐서 연산도 빠르게 수행할 수 있다. 가장 쉬운 예시로 행렬의 전치(transpose)를 생각해보자. 만약 행렬이 2차원 배열처럼 저장되어 있다면 전치 연산은 다음과 같이 수행될 것이다.
- a의 사이즈가 $m\times n$ 이라고할 때, $n\times m$ 크기의 영행렬 생성
- 이중 for 루프를 돌려 $(i,j)$ 원소들을 조회
- 영행렬의 $(j,i)$에 저장
하지만 storage만 사용하면 strides만 뒤짚어주면 전치 연산이 끝나게 된다. 그것이 전치의 정의이기 때문이다. 그림을 참고하자.
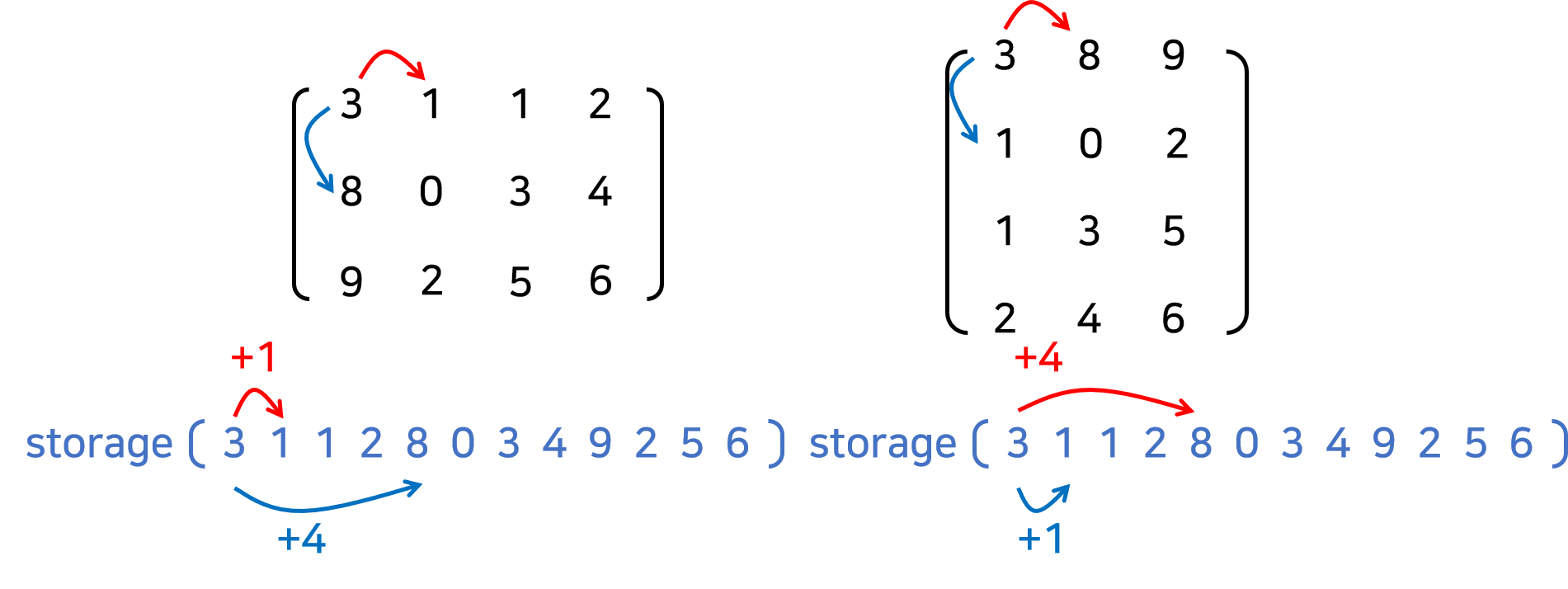
코드로도 확인해보자
a = torch.tensor([[3,1,1,2],
[8,0,3,4],
[9,2,5,6]])
print("============storage==========")
print(a.storage())
print("=============================")
print("Offset: ", a.storage_offset())
print("Strides: ", a.stride())
============storage==========
3
1
1
2
8
0
3
4
9
2
5
6
[torch.LongStorage of size 12]
=============================
Offset: 0
Strides: (4, 1)
b = a.t()
print("============storage==========")
print(b.storage())
print("=============================")
print("Offset: ", b.storage_offset())
print("Strides: ", b.stride())
============storage==========
3
1
1
2
8
0
3
4
9
2
5
6
[torch.LongStorage of size 12]
=============================
Offset: 0
Strides: (1, 4)
전치의 예시를 통해 1차원 배열 storage를 사용하여 효율적인 텐서 연산을 할 수 있다는 것을 알 수 있었다. 다른 연산에 대해서도 다차원 텐서를 사용하는 것보다 storage를 사용하면 더 효율적으로 연산을 수행할 수 있을 것이다. 책에는 전치 연산만 소개하고 있기 때문에 다른 연산은 어떻게 수행되는지에 대해서는 다루지 않도록 하겠다.
결론
이번 포스팅에서는 텐서가 무엇인지 알아보고 텐서를 효율적으로 다루는 방법을 메모리와 자료구조 관점에서 바라보았다. 내 결론은 이거다. 이 책 너무 좋다 ~!
참고한 자료들
[1] Deep learning with Pytorch
[2] StackOverFlow - Python memory consumption in 64 bit system for int and float

