AdamW에 대해 알아보자!
"Decoupled weight decay regularization 논문 리뷰 (1)"

얼마 전에 종료한 Kaggle 대회 “Understanding Clouds from Satellite Images” 에서 우리나라 분(pudae님)께서 자랑스럽게 1등을 하셨다. 정말 친절하게 1등 솔루션을 공유해주셨는데 optimizer로 AdamW를 사용하셨다고 한다. 물론 optimizer의 선택이 우승의 결정적인 요인이라고 할 수는 없겠지만, 다른 상위권 솔루션들이 최근 optimizer 중에서 잘 나가는 RAdam을 사용했기 때문에 AdamW가 무엇인지 궁금해졌다. 그럼 AdamW은 Adam의 어떤 문제점을 해결하며 등장했을까?

Adam은 “optimizer는 묻지도 따지지도 말고 Adam을 사용해라” 라는 격언이 있을 정도로 만능 optimizer처럼 느껴진다. 하지만 만능인 것 치고는 일부 task, 특히 컴퓨터 비젼 task에서는 momentum을 포함한 SGD에 비해 일반화(generalization)가 많이 뒤쳐진다는 결과들이 있었다. AdamW를 소개한 논문 “Decoupled weight decay regularization”에서는 L2 regularization과 weight decay 관점에서 Adam이 SGD이 비해 일반화 능력이 떨어지는 이유를 설명하고 있다.

[서로 다른 initial decay rate와 learning rate에 따른 test error]

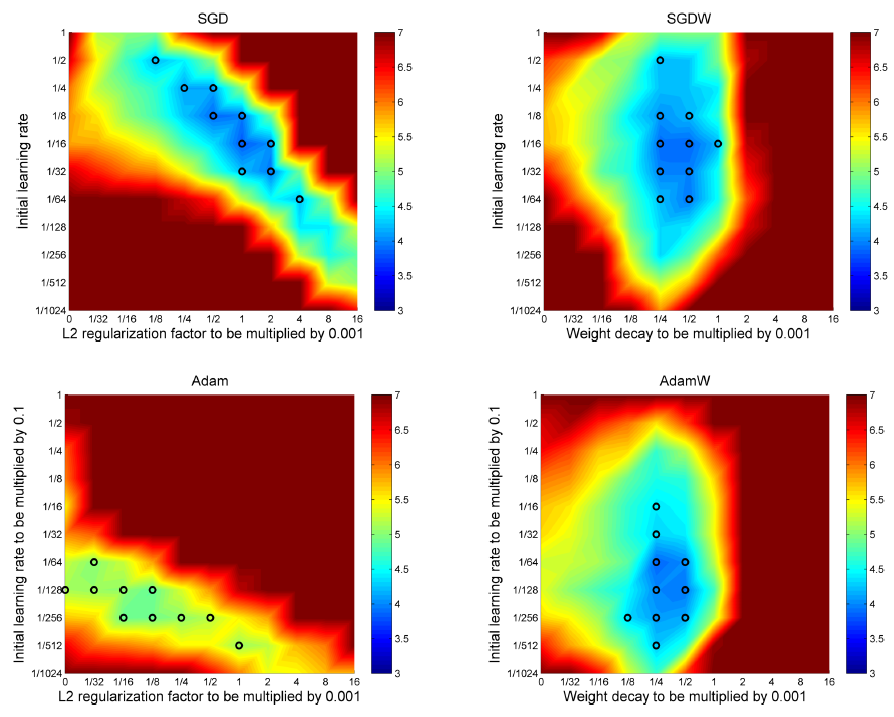
위 그림은 내 마음대로 선정한 이 논문의 메인 figure이다. 그림이 무엇을 나타내는지는 아래에서 자세히 설명하도록 하겠다. 지금은 그림의 색상이 테스트 에러를 나타낸다는 것까지만 알고 있자. 일반적인 SGD와 Adam을 사용했을 때보다 이 논문에서 제안하는 SGDW와 AdamW를 사용했을 때 테스트 에러가 낮은 것을 볼 수 있다. 본격적으로 논문 리뷰에 앞서 이 논문의 핵심 화두인 L2 regularization과 weight decay을 다루고 가자.

들어가기 전에

• 이 post에서 언급하는 SGD는 momentum을 포함한 SGD 이다.
• 이 post는 2부로 나누어서 포스팅할 예정이다.
  • 1부: AdamW에 대해 알아보자! “Decoupled weight decay regularization 논문 리뷰 (1)”
  • 2부: AdamWR에 대해 알아보자! “Decoupled weight decay regularization 논문 리뷰 (2)”

---

L2 regularization

많은 분들이 이미 알고 계시겠지만 L2 regularization은 손실함수에 weight에 대한 제곱텀을 추가해줘서 오버피팅을 방지해주는 방법이다. $t$번 째 미니배치에서의 손실함수를 $f_t$, weight를 $\mathbf{\theta}$라고 하면 L2 regularization을 포함한 손실함수 $f_t^{reg}$는 다음과 같이 나타낼 수 있다.

$$f_t^{reg}(\mathbf{\theta}) = f_t(\mathbf{\theta}) + \frac{\lambda'}{2}\sum_i\theta_i^2$$

$\lambda’$는 regularization 상수로 사용자가 설정하는 하이퍼파라미터이다. 벡터폼에 익숙하신 분들이라면 위 식을 다음과 같이 나타낼 수 있다는 것을 알 수 있을 것이다.

$$f_t^{reg}(\mathbf{\theta}) = f_t(\mathbf{\theta}) + \frac{\lambda'}{2}\mathbf{\theta}^T\mathbf{\theta}$$

L2 regularization이 어떻게 오버피팅을 방지를 해줄 수 있는지를 많이 찾아보았지만 수학적인 답변은 찾을 수가 없었다. 따라서 하나의 예시를 들어 직관적으로 이해를 해보자.

위 사진은 PRML 에서 발췌한 사진이다. 사인 그래프에서 노이즈를 추가하여 샘플링한 데이터를 polynomial regression을 사용해 피팅한 그림이다. $M$은 다항식의 최대차수를 의미한다. 사인 그래프를 9차 다항식으로 피팅했을 때 다항식의 각 계수는 오른쪽 표의 가장 오른쪽 열에 나타나있다. 그 값이 굉장히 큰 것을 알 수 있다. 굳이 weight를 증가시켜가면서까지 local noise에 반응한 것으로 생각할 수 있다. 한편, weight가 굉장히 클 경우 데이터가 아주 조금만 달라져도 예측 값이 굉장히 민감하게 바뀌게 된다. 오버피팅된 모델에 훈련 데이터와 다른 테스트 데이터가 들어갔을 때 에러가 큰 이유이다.

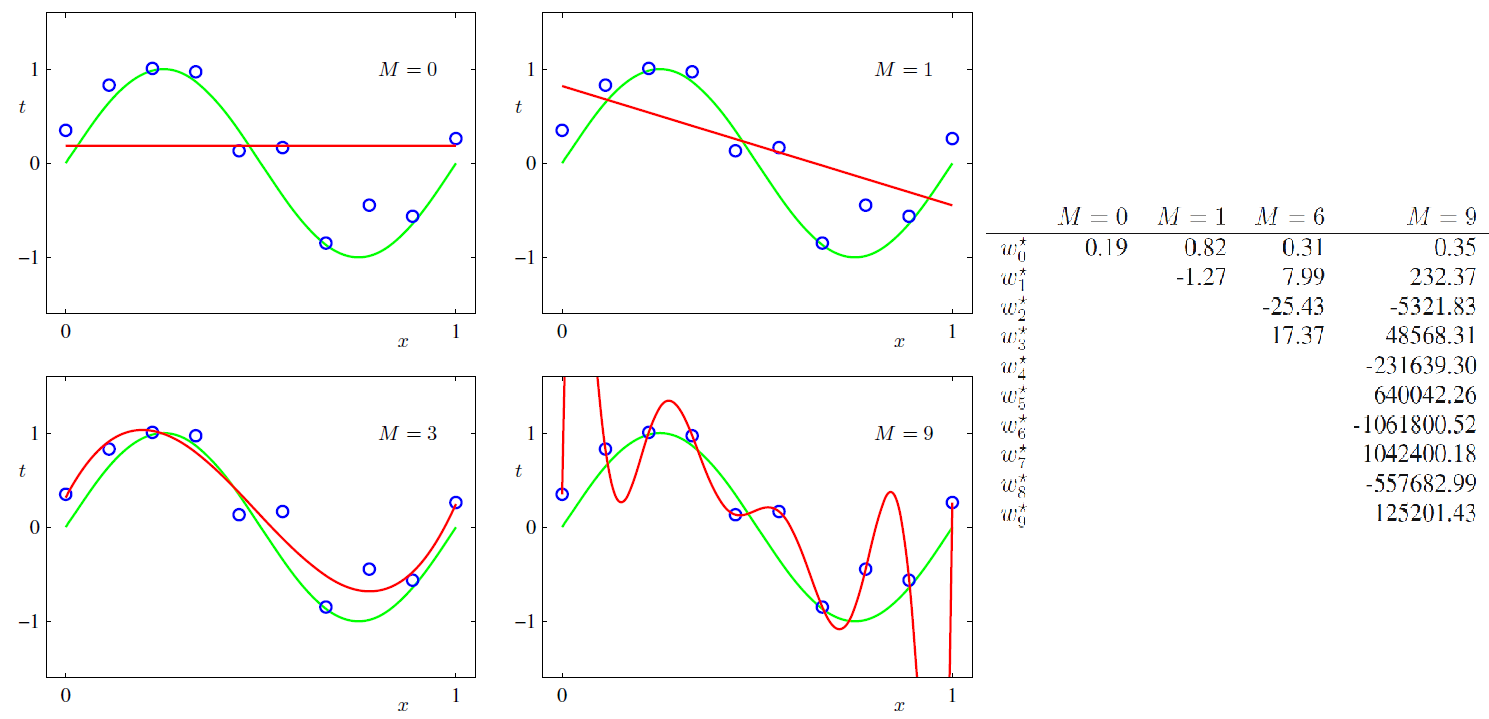
손실함수에 L2 regularization을 추가해줌으로써 weight가 비상식적으로 커지는 것을 방지할 수 있다. 손실함수를 최소로 만들어주는 것이 목표인데 weight 값이 커지게 되면 $\mathbf{\theta}^T\mathbf{\theta}$ 값이 커져서 손실함수가 커지게 되기 때문이다. 따라서 weight가 너무 커지지 않는 선에서 원래의 손실함수를 최소로 만들어주는 weight를 찾게 되는 것이다.

---

Weight Decay

weight decay는 gradient descent에서 weight 업데이트를 할 때, 이전 weight의 크기를 일정 비율 감소시켜줌으로써 오버피팅을 방지한다. 원래 gradient descent 업데이트 식은 다음과 같다.

$$\mathbf{\theta}_{t+1} = \mathbf{\theta}_{t} - \alpha \nabla f_t(\mathbf{\theta}_{t})$$

$\alpha$는 learning rate이다. 한편, weight decay를 포함하면 다음과 같은 업데이트 식을 사용한다.

$$\mathbf{\theta}_{t+1} = (1-\lambda)\mathbf{\theta}_{t} - \alpha \nabla f_t(\mathbf{\theta}_{t})$$

$\lambda$는 decay rate라고 부르며 사용자가 0과 1사이 값으로 설정하는 하이퍼파라미터이다. weight를 업데이트할 때 이전 weight의 크기를 일정 비율만큼 감소시키기 때문에 weight가 비약적으로 커지는 것을 방지할 수 있다.

---

L2 Regularization = Weight decay?

많은 책과 자료에서 L2 regularization 과 weight decay는 서로 같은 것이라고 말한다. 그럼 과연 L2 regularization과 weight decay는 정말 같은 것일까? 정답은 일부는 맞고 일부는 틀리다. SGD에 대해서는 맞지만 Adam에 대해서는 틀리다. Adam을 포함한 adaptive learning rate를 사용하는 optimizer들은 SGD와 다른 weight 업데이트 식을 사용하기 때문이다. L2 regularization이 포함된 손실함수를 Adam을 사용하여 최적화할 경우 일반화 효과를 덜 보게 된다.

Case 1. SGD

먼저, L2 regularization이 포함된 손실함수에 SGD를 적용한 weight 업데이트 식은 다음과 같다.

$$\mathbf{\theta}_{t+1} = \mathbf{\theta}_{t} - \alpha \nabla f_t^{reg}(\mathbf{\theta}_{t})$$

이 때, L2 regularization이 포함된 손실함수 $f_t^{reg}(\mathbf{\theta})$를 편미분하면 다음과 같다.

$$\nabla f_t^{reg}(\mathbf{\theta}) = \nabla f_t(\mathbf{\theta}) + \lambda' \mathbf{\theta} $$

이를 weight 업데이트 식에 대입하면 다음과 같다.

$$ \begin{matrix} \mathbf{\theta}_{t+1} & = & \mathbf{\theta}_{t} - \alpha \nabla f_t^{reg}(\mathbf{\theta}_{t}) \\\ & = & \mathbf{\theta}_{t} - \alpha (\nabla f_t(\mathbf{\theta}_t) + \lambda' \mathbf{\theta}) \\\ & = & (1-\alpha\lambda')\mathbf{\theta}_{t} - \alpha \nabla f_t(\mathbf{\theta}) \end{matrix} $$

만약, $\lambda’ = \frac{\lambda}{\alpha}$ 라면 L2 regularization은 정확히 weight decay와 같은 역할을 한다. 여기서 주목해야할 또 다른 포인트는 $\lambda’ = \frac{\lambda}{\alpha}$에서 regularization 상수 $\lambda’$이 learning rate $\alpha$에 dependent하다는 것이다. 만약 사용자가 일반화 능력이 가장 좋은 regularization 상수 $\lambda’$을 찾았다고 하자. 그런데 이 때 learning rate $\alpha$를 바꾸면 더 이상 $\lambda’$가 최적의 하이퍼파라미터가 아닐 수도 있다는 것을 의미한다.

---

Case 2. Adam

Adam을 빠르게 짚고 넘어가보자. Adam은 gradient의 1차 모먼트 $m_t$와 2차 모먼트 $v_t$를 사용하여 모멘텀 효과와 weight마다 다른 learning rate를 적용하는 adaptive learning rate 효과를 동시에 보는 최적화 알고리즘이다.

$$ \begin{matrix} m_t & = & \beta_1 m_{t-1} + (1-\beta_1)\nabla f_t(\mathbf{\theta}_t) \\\ v_t & = & \beta_2 v_{t-1} + (1-\beta_2)\nabla f_t(\mathbf{\theta}_t)^2 \\\ \hat{m_t} & = & \frac{m_t}{1-\beta_1^t} \;\;\; \text{(Bias correction)}\\\ \hat{v_t} & = & \frac{v_t}{1-\beta_2^t} \;\;\; \text{(Bias correction)}\\\ \mathbf{\theta}_{t+1} & = & \mathbf{\theta}_{t} - \frac{\alpha}{\sqrt{\hat{v_t}} + \epsilon}\hat{m_t} \end{matrix} $$

Adam은 위와 같이 weight 업데이트를 해준다. Adam에서는 L2 regularization과 weight decay가 다르다는 것을 보이기 위해 weight 업데이트 식을 다음과 같이 간략하게 표현해보자.

$$\mathbf{\theta}_{t+1} = \mathbf{\theta}_{t} - \alpha M_t \nabla f_t^{reg}(\mathbf{\theta}_t)$$

SGD에서 구한 $\nabla f_t^{reg}(\mathbf{\theta})$을 대입해보자. $$ \begin{matrix} \mathbf{\theta}_{t+1} & = & \mathbf{\theta}_{t} - \alpha M_t \nabla f_t^{reg}(\mathbf{\theta}_{t}) \\\ & = & \mathbf{\theta}_{t} - \alpha M_t (\nabla f_t(\mathbf{\theta}_t) + \lambda' \mathbf{\theta}) \\\ & = & \mathbf{\theta}_{t} - \alpha \lambda' M_t \mathbf{\theta} - \alpha M_t \nabla f_t(\mathbf{\theta}_t) \end{matrix} $$

반면, weight decay만 적용한 weight 업데이트 식은 다음과 같다.

$$\mathbf{\theta}_{t+1} = (1-\lambda)\mathbf{\theta}_{t} - \alpha M_t \nabla f_t(\mathbf{\theta})$$

이 둘은 $M_t = kI$가 아닌 이상은 같지 않을 것이다. $\lambda’$ 앞에 $M_t$가 붙기 때문에 SGD 경우보다 $\lambda’$가 더 작은 decay rate로 weight decay 역할을 하게 된다. 따라서 일반화 능력이 SGD보다 작게 된다고 저자는 주장하고 있다.

---

SGDW 와 AdamW

위에서 L2 regularization를 사용하면 weight decay 효과를 볼 수 있다는 것을 확인했다. 그리고 Adam의 경우 그 효과를 덜 받게 되는 것도 확인해보았다. 저자는 L2 regularzation에 의한 weight decay 효과 뿐만 아니라 weight 업데이트 식에 직접적으로 weight decay 텀을 추가하여 이 문제를 해결한다. L2 regularization과 분리된 weight decay라고 하여 decoupled weight decay라고 말하는 것이다.

SGDW와 AdamW의 알고리즘이다. 지금까지 설명하지 않았던 $\eta$가 있는데 이는 매 weight 업데이트마다 learning rate를 일정 비율 감소시켜주는 learning rate schedule 상수를 의미한다. 초록색으로 표시된 부분이 없다면 L2 regularization을 포함한 손실함수에 SGD와 Adam을 적용한 것과 똑같다. 하지만 초록색 부분을 직접적으로 weight 업데이트 식에 추가시켜줌으로써 weight decay 효과를 볼 수 있게 만들었다.

---

실험 결과들

저자는 Shake-Shake regularization에서 수행한 실험을 벤치마킹하여 자신의 가설들을 검증하였다. 자세한 실험 환경을 알기 위해서는 위 논문을 읽어야하기 때문에 저자가 언급한 정도로만 실험 환경을 소개하겠다.

사용한 데이터들

• CIFAR-10
• ImageNet의 다운샘플 버전(32 x 32 이미지 120만 장)

모델 구조: Shake-Shake regularization 모델 (feature map을 augmentation 해주는 residual branch라는 구조를 갖고 있음)

• 26 2x64d ResNet
  • 깊이 26
  • 2개의 residual branch
  • 첫 번째 residual branch의 filter 수 64개,
  • 총 파라미터 11.6M
• 26 2x96d ResNet
  • 깊이 26
  • 2개의 residual branch
  • 첫 번째 residual branch의 filter 수 96개,
  • 총 파라미터 25.6M

기타

• batch size = 128
• regular data augmentation

---

Experiment 1. 서로 다른 learning rate schedule 에서의 Adam과 AdamW 성능 비교

이 실험은 L2 regularization에 Adam을 적용했을 때와 weight decay까지 추가한 AdamW의 성능을 비교하는 실험이다. 이 논문에서 일반적인 learning rate schedule 에서 작동하는 알고리즘을 제안했기 때문에 다음과 같이 서로 다른 세 가지 lr schedule 에 대해서도 실험을 진행하였다. (Learning rate schedule는 2부에서 다루고 있습니다.)

• fixed learning rate
• step-drop learning rate
• cosine annealing

[다양한 learning rate와 L2 regularization 상수(AdamW일 경우 weight decay) 조건에서
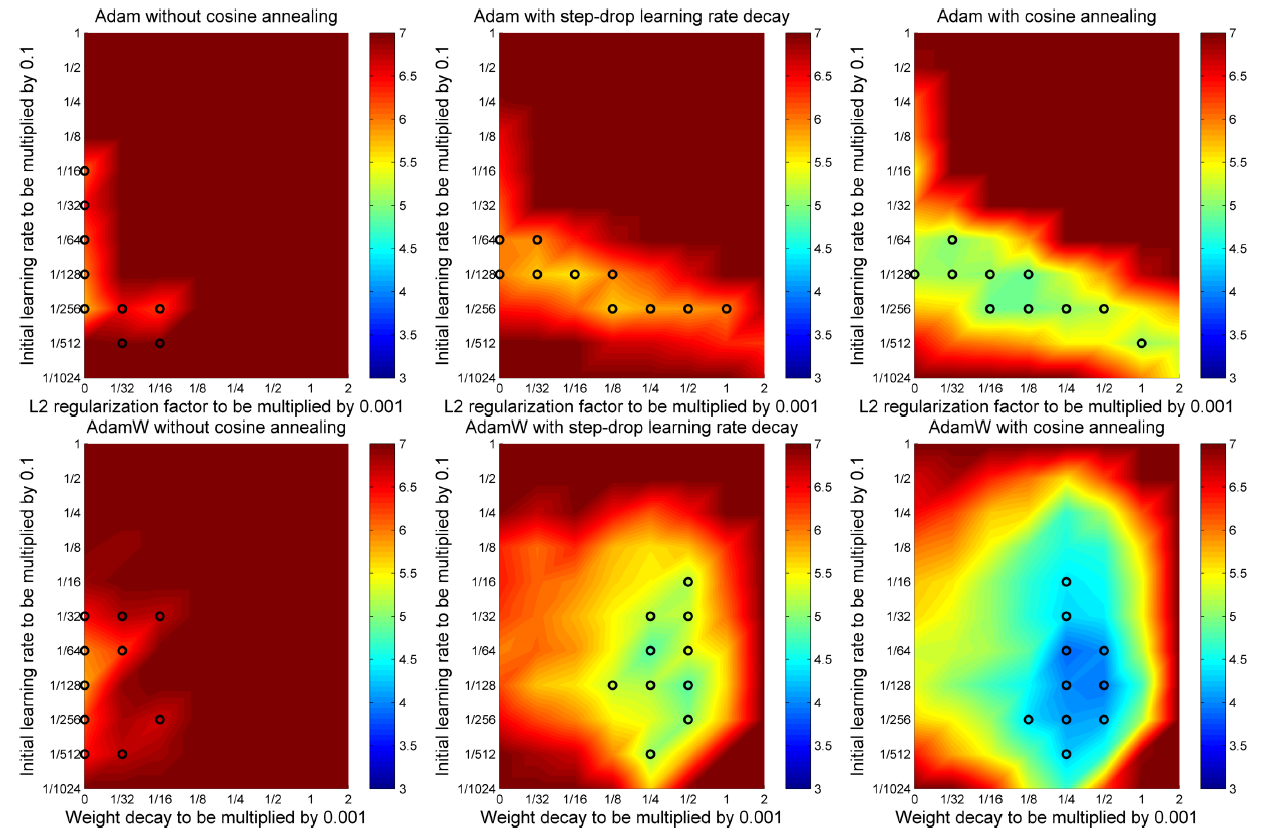
CIFAR-10 데이터를 26 2x64d ResNet으로 100 epochs 학습했을 때 test error를 나타내는 그림.
1행: Adam, 2행: AdamW, 1열: fixed lr, 2열: step-drop learning rate, 3열: cosine annealing
x축: L2 regularization 상수(AdamW일 경우 weight decay), y축: learning rate 초기값,
성능이 가장 좋았던 상위 10개의 실험을 검은색 원으로로 표시하였다.]

실험 환경: CIFAR-10, 26 2x64d ResNet, 100 epohcs

결과 해석

• Adaptive learning rate를 사용하는 Adam은 weight마다 다른 lr을 적용하기 때문에 lr schedule의 중요성이 떨어지는 것처럼 보이지만 적절한 lr schedule을 사용하면 더 좋은 성능을 얻을 수 있다.
  • 특히, cosine annealing이 가장 좋은 성능을 보인다.
• AdamW가 Adam보다 모든 lr schedule에 대해 좋은 성능을 얻었다.
• AdamW의 하이퍼파라미터 공간이 더 잘 구분된다.
• 이후 실험은 모두 cosine annealing을 적용한다.

---

Experiment 2. SGD vs SGDW , Adam vs AdamW

Experiment 2는 내 마음대로 선정했었던 main figure에 대한 실험이다. 기본적으로 Experiment 1과 같은 실험 환경에서 SGD와 SGDW가 추가된 실험이다.

[다양한 learning rate와 L2 regularization 상수(혹은 weight decay) 조건에서
CIFAR-10 데이터를 26 2x64d ResNet으로 100 epochs 학습했을 때 test error를 나타내는 그림.]

결과 해석

• Decoupled weight decay를 적용하지 않고 오직 L2 regularization만 사용할 경우 (1열), 성능 상위 10개의 하이퍼파라미터 (검은색 원)가 대각선으로 분포하는 것을 볼 수 있다. 이는 L2 regularization만 사용했을 때 얻을 수 있는 weight decay 효과가 learning rate에 종속되어 있기 때문이다.($\lambda’=\frac{\lambda}{\alpha}$)
  • 따라서, 최적의 하이퍼파라미터를 찾기 위해서는 $\alpha$와 $\lambda$를 동시에 바꿔줘야 한다.
  • 1행 1열의 가장 왼쪽 위의 검은 원($\alpha = 1/2, \lambda = 1/8*0.0001$)에서 HP 튜닝을 할 때, $\alpha$나 $\lambda$ 중 하나만 바꿔가면 성능이 더 안 좋아질 것이다. 더 좋은 성능을 얻기 위해서는 $\alpha$와 $\lambda$를 동시에 바꿔주어야 한다.
  • SGD가 하이퍼파리미터에 민감하다는 평판이 있는데 이러한 이유 때문이다.
• 반대로 decoupled weight decay를 사용할 경우 learning rate와 weight decay가 서로 독립적이다. 이 말은 어느 한 하이퍼파라미터를 고정하고 다른 하나만을 바꿔가도 더 좋은 성능을 얻을 수 있다는 뜻이다.
• 둘 다 L2 regularization을 사용했는데도 Adam의 결과는 확실하게 SGD보다 안 좋다.
  • Adam은 $\lambda = 0$일 때나 $\lambda \ne 0$ 일 때나 검은 원이 있는 성능이 비슷하다. 즉, Adam은 L2 regularization의 효과를 덜 받는다.
• AdamW는 SGD와 SGDW와 필적할 만한 성능을 보였다.

---

Experminet 3. AdamW와 Adam의 일반화(Generalization) 능력 비교

Experiment 3에서는 AdamW와 Adam의 일반화 능력을 비교하는 실험이다.

[1행: Epochs에 따른 Adam과 AdamW의 훈련 손실(1열) / 테스트 에러(2열)
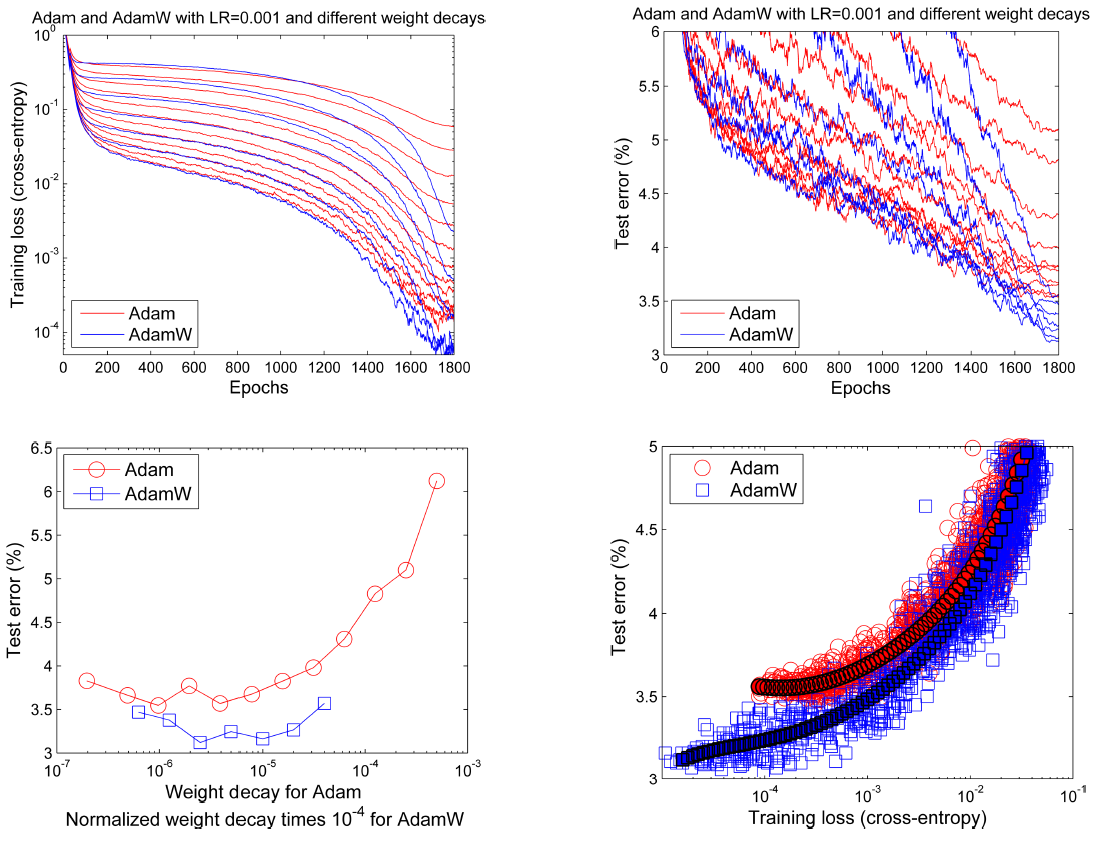
2행 1열: $\lambda$값에 따른 Adam과 AdamW의 테스트 에러
2행 2열: 훈련 손실과 테스트 에러]

실험 환경: CIFAR-10, 26 2x96d ResNet, Epochs 1800, learning rate = 0.001, normalized weight deacy 사용 (Normalied weight decay는 2부에서 다루고 있습니다.)

결과 해석

• 학습 초기에는 Adam과 AdamW과 비슷한 loss를 보이지만 학습이 진행될 수록 AdamW의 훈련 손실과 test 에러가 더 낮아진다.
• 2행 2열의 그래프에서 같은 훈련 손실에 대해서 AdamW의 테스트 에러가 더 낮은 것을 볼 수 있다.
  • 즉, AdamW의 좋은 성능이 단순히 학습 동안 더 좋은 수렴 지점을 찾았기 때문이 아니라, 더 좋은 일반화 능력이 있기 때문이다.

---

2부 소개

2부에서는 이 논문의 저자가 2016년에 발표했던 논문 “SGDR: Stochastic Gradient Descent with Warm Restarts” 에서 다루고 있는 cosine annealing과 warm start에 대해 알아보고 이를 AdamW에 적용한 AdamWR에 대해서 알아보도록 하겠습니다. (솔직히 언제 돌아올지는 모르겠습니다. ㅎㅎ