위상수학을 이용한 데이터 시각화 Mapper

Mapper는 고차원 데이터를 2차원으로 시각화할 수 있는 시각화 기법이다. 고차원 데이터를 시각화하기 위해서는 PCA나 t-SNE 등의 차원축소 기법들이 많이 사용되지만, 이들과 다르게 Mapper는 주어진 데이터를 그래프 자료구조로 변환하여 시각화한다. 데이터를 그래프 자료구조로 변환하는 아이디어 뒤에 위상수학적 배경이 있기 때문에 Mapper는 위상수학적 데이터 분석 (Topological data analysis; TDA) 분야로 구분된다.

TDA는 주어진 데이터가 어떠한 위상공간에서 샘플링되었다는 가정으로부터 시작된다. 우리의 목표는 주어진 데이터로부터 해당 위상공간의 모양과 성질을 분석하는 것이다. 통계학에서 표본 (데이터)으로부터 모집단 (위상공간)을 추정하는 것을 비유로 들 수 있다. 하지만 데이터는 이산적 (discrete)이고 위상공간은 연속적 (continuous)인데 어떻게 데이터로부터 위상공간의 특징을 알아낼 수 있을까?

주어진 데이터로 위상공간을 근사하기 위해서 우리는 먼저 데이터로부터 Simplicial complex (단체 복합체)라는 것을 만들어준다. Simplicial complex는 simplex (단체)들을 모아놓은 것으로 0-simplex는 점, 1-simplex는 선, 2-simplex는 삼각형, 3-simplex는 정사면체, n-simplex는 꼭지점이 $n+1$개인 $n$차원 다면체이다. (그림1) 은 가장 왼쪽부터 순서대로 0-simplex부터 3-simplex를 나타내며 가장 오른쪽 그림은 Simplicial complex의 예시이다.

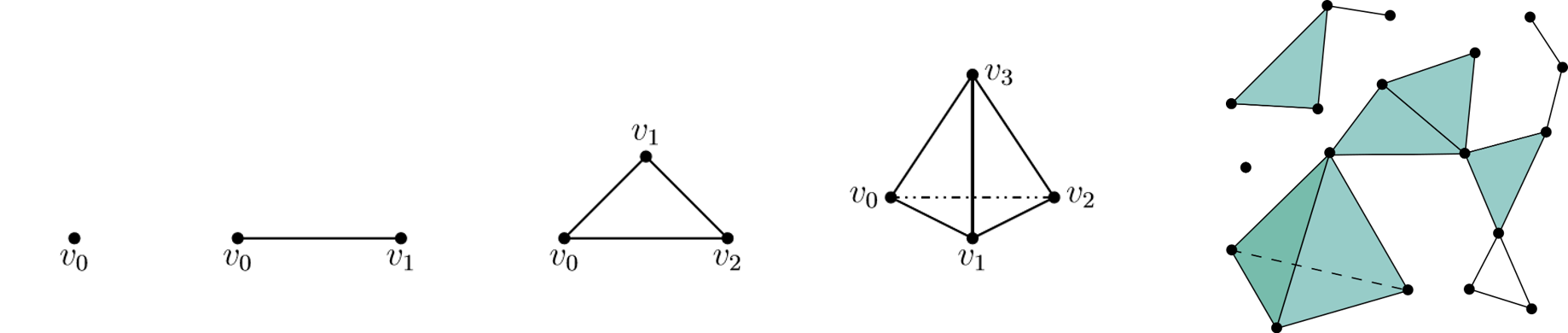
데이터로부터 적절한 simplicial complex를 만들게 되면, 우리는 그것의 형태나 성질을 분석하여 데이터가 추출된 공간을 추정하게 된다. 예를 들어, (그림1) 에 있는 simplicial complex는 다섯시 방향에 구멍 (hole)이 하나 있다. 세 개의 1-simplex (선)이 만나 구멍이 있는 삼각형을 만든 것이다. 이를 통해 데이터가 추출된 위상공간에는 구멍이 하나 있을 것이라고 예상하는 것이다.

따라서 TDA에서는 Simplicial complex를 어떻게 만들 것인지가 가장 중요한 요소이다. 보통 Simplicial complex는 특정 거리 $r$을 설정하고 두 데이터 사이의 거리가 $r$ 미만이면 연결하는 방식으로 만드는 것이 일반적이다. Mapper에서는 이후 설명할 방법과 같이 그래프를 만들게 되는데, 만들어진 그래프를 데이터의 Simplicial complex으로 생각하는 것이다.

Mapper가 그래프를 그리는 방법

데이터와 각 데이터에 대한 filter 함수의 값이 주어졌다고 가정하자.

• Let $X=\{\mathbf{x}_i\}_{i=1}^N$ and $\{f(\mathbf{x}_i)\}_{i=1}^N$ be given.
• filter 함수는 사용자가 정의하기 나름이며 모든 데이터에 값이 부여되기만 하면 된다. 주로 데이터의 좌표를 filter 함수로 사용한다.

filter 함수값의 범위를 구한다.

• Let $m:=\underset{i=1,\cdots,N}{\min} f(\mathbf{x}_i)$, $M:=\underset{i=1,\cdots,N}{\max} f(\mathbf{x}_i)$. Then, $m \le f(\mathbf{x}_i)\le M$ for $i=1,\cdots,N$

filter 함수값의 범위를 적당한 길이를 갖는 중복된 구간들로 나눠준다.

• Divide the range $I$ into a set of smaller intervals $S=\{I_j\}_j$
• Example) $I=[0,2]$을 길이($l$)가 1이고, 중복률($p$)이 $2 \over 3$인 구간들로 나누면 $S=\{[0,1],[0.33,1.33],[0.66, 1.66],[1,2]\}$이 된다.

각 구간의 inverse image를 구한다.

• For each interval $I_j$, find the inverse image $X_j = \{ \mathbf{x} \vert f(\mathbf{x}) \in I_j\}$

각 inverse image를 다시 연결된 (path-connected) 구간으로 분할한다.

• For each smaller set $X_j$, decomopose $X_j$ into path-connected sets $X_{j,k}$
• 이 단계는 군집화 기법을 사용하여 수행된다.

각 구간을 노드로 선택하고, 각 구간에 동일한 데이터가 속해있을 경우 엣지를 연결한다.

• Treat each $X_{j,k}$ as a vertex and draw edge between vertices whenever $X_{j,k} \cap X_{l,m} \ne \emptyset$

Example 1)

데이터와 filter 함수

• 데이터: 평균이 0이고, 표준편차가 1인 정규분포에서 샘플링한 100개의 1차원 데이터
• filter 함수: $f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$,

filter 함수값의 범위

• $0 \le f(x) \le \frac{1}{\sqrt{2\pi}}\approx 0.4$

filter 함수값의 범위를 중복된 4개 구간으로 나눠준다.

• $S=\{[0, 0.1], [0.05, 0.2], [0.15, 0.3], [0.25, 0.4]\}$

4개 구간에 대해 inverse image를 구한다.

• 각 구간에 해당하는 inverse image는 (그림2_1)과 같다.

각 inverse image를 다시 연결된 구간으로 분할

• $[0.25, 0.4]$의 inverse image는 하나의 connected set이고, 이 외 구간의 inverse image는 2개의 connected set 을 갖는다.

각 구간을 노드로 선택 및 동일한 데이터가 속한 구간 연결

• 중복된 데이터를 갖는 구간을 서로 연결해주어 엣지를 만든다.
• 최종적인 그래프는 (그림2_2)와 같다.
  • 이 때, 색상은 filter 함수의 함수값, 크기는 포함된 데이터의 개수를 의미한다.

Example 2)

데이터와 filter 함수

• 데이터: $\mathcal{N}_2(\mathbf{0}, I)$에서 샘플링한 100개 2차원 데이터
• filter 함수: $f(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}$

filter 함수값의 범위

• $0 \le f(x,y) \le \frac{1}{2\pi} \approx 0.16$

filter 함수값의 범위를 중복된 4개 구간으로 나눠준다.

• $S=\{[0, 0.04], [0.03, 0.08], [0.07, 0.12], [0.11, 0.16]\}$

4개 구간에 대해 inverse image를 구한다.

• 각 구간에 해당하는 inverse image는 (그림1)과 같다.

각 inverse image를 다시 연결된 구간으로 분할

• 각 구간의 inverse image는 모두 하나의 connected set이기 때문에 4개의 노드가 만들어진다.

각 구간을 노드로 선택 및 동일한 데이터가 속한 구간 연결

• 중복된 데이터를 갖는 구간을 서로 연결해주어 엣지를 만든다.
• 최종적인 그래프는 (그림2)와 같다.

Giotto-tda를 사용한 Mapper

Mapper를 사용할 수 있는 파이썬 패키지는 KeplerMapper와 Giotto-tda가 있다.

• KeplerMapper는 굉장히 완성도가 있는 Mapper 패키지이다. 특히, 시각화 결과를 *.d3 형식으로도 제공하기 때문에 매우 근사한 interactive한 시각화가 가능하다. Mapper만 사용할 경우 KeplerMapper 사용을 추천한다.
• Giotto-tda의 결과물은 상대적으로 근사하지는 않지만, Giotto-tda에서 제공하는 persistent homology 기법들과 Mapper를 결합할 수 있다는 장점이 있다.

두 패키지 문법은 서로 유사하기 때문에 둘 다 사용해보고 자신에게 맞는 패키지를 선택하는 것을 권장한다. 이번 포스트에서는 giotto-tda를 사용하였다.

필요라이브러리 불러오기

import numpy as np
import matplotlib.pyplot as plt

# giotto-tda
import gtda.mapper

from sklearn.datasets import make_circles
from sklearn.cluster import DBSCAN

데이터 불러오기 및 시각화

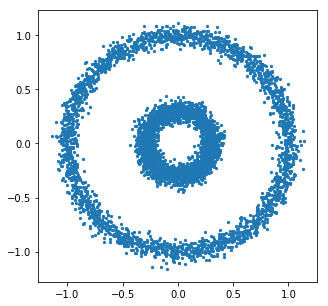
• sklearn.datasets의 make_circles를 사용

X, _ = make_circles(n_samples=5000, noise=0.05, factor=0.3, random_state=42)


plt.figure(figsize = (5,5))
plt.scatter(X[:,0], X[:,1], s=5)
plt.show()

Mapper

1. filter 함수는 가장 단순한 2개를 사용하였으며 각각 데이터의 x좌표와 y좌표를 나타내는 함수이다.
   • 즉, $f_1(x,y)=x, f_2(x,y)=y$
   • gtda.mapper.Projection
2. filter 함수값의 범위를 중복된 구간으로 나누는 것을 cover라고 하며 가장 단순한 방법이 CubicalCover이다. CubicalCover는 1차원 직선은 구간으로, 2차원 평면은 사각형으로, 3차원 공간은 정육면체로 나누는 방법이다.
   • gtda.mapper.CubicalCover
3. 군집화 알고리즘은 DBSCAN을 사용하였으며, fit_transform 메서드가 있는 scikit-learn 군집화 알고리즘이면 모두 가능하다.
   • 하지만, DBSCAN처럼 군집 개수를 지정해주지 않는 알고리즘 사용을 권장한다.
   • 논문에서 언급한 추후 필요 연구 중 하나

# 1. Filter function
filter_func = gtda.mapper.Projection(columns=[0, 1])

# 2. Cover
cover = gtda.mapper.CubicalCover(n_intervals=10, overlap_frac=0.3)

# 3. Clustering
clusterer = DBSCAN()

pipe = gtda.mapper.make_mapper_pipeline(filter_func=filter_func,
                                        cover=cover,
                                        clusterer=clusterer,
                                        verbose=False)

fig = gtda.mapper.plot_static_mapper_graph(pipe, X)
fig.show()

결과 그림은 원래 데이터셋이 큰 원과 작은 원을 갖고 있는 것을 포착할 수 있다. 하지만 mapper는 결국 graph를 시각화하는 것이기 때문에 그림의 노드들은 위치 정보가 없다. 따라서 큰 원과 작은 원의 위치 관계는 포착할 수 없다는 한계점이 있다.

출처

• figure1_1: https://themodularperspective.com/2019/03/11/a-crash-course-in-homology-part-i-delta-complexes/
• figure1_2: https://en.wikipedia.org/wiki/Simplicial_complex
• figure2_2: https://research.math.osu.edu/tgda/mapperPBG.pdf
• 예제: https://giotto-ai.github.io/gtda-docs/latest/notebooks/mapper_quickstart.html