
강화학습 공부를 하신 분들이라면 TRPO 논문을 읽어보진 않았어도 TRPO 논문이 극악의 난이도를 자랑한다는 것을 알고 있을 것이다. 내용이 어렵다고 논문을 읽지 않기에는 너무나도 많은 논문에서 TRPO를 인용하고 비교 알고리즘으로 사용한다. “피할 수 없으면 즐겨라”라는 말이 있다. 그래 이제 즐길 때가 왔다. 그런데 논문을 펼치니 즐겁지 않다. 논문을 덮을까…?
- 제목: Trust Region Policy Optimization
- 저자: Schulman, John, Sergey Levine, Pieter Abbeel, Michael Jordan, Philipp Moritz, Berkeley
- 연도: 2015
- 링크: https://proceedings.mlr.press/v37/schulman15.html
다음 링크에서 본 포스팅의 PDF 파일 버전을 다운 받아서 볼 수 있습니다.
- https://github.com/HiddenBeginner/hiddenbeginner.github.io/tree/master/static/pdf/2022-9-18-trpo.pdf
이 논문은 policy monotonic improvement를 위한 대여정
나는 TRPO 논문을 위의 한 문장으로 요약하고 싶다. 모두 잘 알다시피 general policy iteration은 두 단계로 구성되어 있다.
- 주어진 정책의 가치함수를 계산하는 policy evaluation 단계
- 가치함수를 바탕으로 정책을 개선하는 policy improvement 단계
TRPO 논문은 policy improvement 단계에서 어떻게 하면 정책을 monotonically improve할 수 있을까에 대한 논문이다. 우리는 policy improvement 단계를 다음과 같이 기억하고 있을 것이다.
유한 상태 공간 $\mathcal{S}$, 유한 행동 공간 $\mathcal{A}$일 경우 모든 $(s, a)$ 순서쌍에 대한 정책의 행동가치함수 $Q_{\pi}(s, a)$를 계산하고 이를 policy improvement에 사용한다. \[\pi_{\text{new}}(s)=\operatorname*{argmax}_{a \in \mathcal{A}} Q_{\pi_{\text{old}}} (s, a), \;\forall s \in \mathcal{S}. \quad \quad (1)\]
식 $(1)$의 방식으로 정책을 개선하면, 매 업데이트마다 정책의 성능이 동일하거나 더 좋아지는 monotonic improvement가 보장되고, 업데이트를 반복하면 결국 최적의 정책에 수렴한다는 것을 잘 알고 있다.
하지만 상태 공간과 행동 공간이 large scale이거나 continuous하다면, 우리는 모든 순서쌍 $(s, a)$를 고려하기 어려울 뿐만 아니라 $\operatorname{argmax}$를 구할 수 없어서 식 $(1)$을 사용할 수 없다. 이 경우 우리는 function approximation을 사용하며 행동가치함수를 추정하거나 정책을 모델링하게 된다. 하지만 이러한 approximation은 결국 추정에 대한 오차를 발생시키기 때문에 monotonic improvement를 더 이상 보장할 수 없다.
이 논문에서는 large scale MDP에서도 정책을 monotonically improve할 수 있는 방법을 제안한다. 그 과정은 다음과 같다.
- 사전연구에서 증명한 개선된 정책 $\pi_{\text{new}}$의 성능의 lower bound 소개 및 한계점 제시
- 한계점을 해결하기 위한 방법 제시
- 복잡한 이론을 근사하는 구현적 방법론 소개
사실 1번 잘 이해해도 2번, 3번은 술술 이해할 수 있는 것 같다. 이번 포스팅도 1번을 설명하는데 많은 분량을 차지할 것 같다.
사전연구: Conservative policy iteration (CPI)
사용할 표기들
우선 사전 연구를 설명하기 위해 여러가지 표기에 익숙해지자.
우리가 풀고 싶은 순차적 의사 결정 문제는 $MDP( \mathcal{S}, \mathcal{A}, P, r, \rho_0, \gamma)$로 정의될 수 있다. $\mathcal{S}$는 상태 공간, $\mathcal{A}$ 는 행동 공간, $P:\mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow [0,1]$는 전이확률분포, $r: \mathcal{S} \rightarrow \mathbb{R}$ 은 보상함수 $\rho_0: \mathcal{S} \rightarrow [0,1]$ 은 초기 상태의 확률분포, $\gamma$는 할인률이다.
정책 $\pi: \mathcal{S} \times \mathcal{A} \rightarrow [0,1]$ 은 상태 $s$에서 행동 $a$를 취할 확률을 나타낸다. 우리는 누적할인보상의 기댓값을 최대로 만들어주는 정책을 찾고 싶다. 주어진 정책 $\pi$ 의 누적할인보상의 기댓값을 다음과 같이 적어줄 수 있다. \[\begin{matrix} \eta(\pi)=\mathbb{E}_{s_0,a_0,s_1,a_1, \cdots}\left[ \sum\limits_{t=0}^{\infty} \gamma^t r(s_t)\right], \text{where} \\ s_0 \sim \rho_0, \; a_t \sim \pi(a_t|s_t), \; s_{t+1} \sim P(s_{t+1}|s_t, a_t). \end{matrix}\]
위 수식이 누적할인보상의 기댓값을 컴팩트하게 잘 나타낸 것 같다. 정책 $\pi$ 의 초기 상태의 상태가치함수의 기댓값이기도 하다.
한편, 주어진 정책 $\pi$의 상태가치함수 $V_{\pi}:\mathcal{S}\rightarrow\mathbb{R}$, 행동가치함수 $Q_{\pi}:\mathcal{S}\times \mathcal{A} \rightarrow\mathbb{R}$, 그리고 advantage 함수 $A_{\pi}: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$는 다음과 같이 정의된다. \[\begin{matrix} V_{\pi}(s_t) = \mathbb{E}_{a_t, s_{t+1}, a_{t+1}, \cdots} \left[ \sum\limits_{l=0}^{\infty} \gamma^{l} r(s_{t+1})\right], \\ Q_{\pi}({s_t, a_t}) = \mathbb{E}_{s_{t+1}, a_{t+1}, \cdots} \left[ \sum\limits_{l=0}^{\infty} \gamma^{l} r(s_{t+1})\right], \\ A_{\pi}(s_t, a_t) = Q_{\pi}(s_t, a_t) - V_{\pi}(s_t), \text{ where } \\ a_t \sim \pi(a_t | s_t), \; s_{t+1} \sim P(s_{t+1}|s_{t}, a_{t}) \text{ for } t\ge0. \end{matrix}\]
두 정책의 성능 사이의 관계식
지금까지는 모두 익숙한 개념일 것이다. 앞으로 나올 개념은 다소 생소할 수 있다. 우리의 목표는 monotonic improvement이다. 정책의 성능이 향상되었는지 알기 위해서는 $\eta({\pi_{\text{new}}})$ 와 $\eta(\pi_{\text{old}})$ 를 각각 구해서 비교하면 될 것이다. 하지만 우리는 둘 다 구하는 대신 $\eta({\pi_{\text{new}}})$와 $\eta(\pi_{\text{old}})$의 관계식을 구할 것이다. 결론부터 말하자면 아무 두 정책 $\pi$와 $\tilde{\pi}$이 주어졌을 때, 정책 $\tilde{\pi}$의 성능지표를 $\pi$의 성능지표에 대한 관계식으로 적어줄 수 있다. \[\eta(\tilde{\pi})=\eta(\pi) + \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t} A_{\pi}(s_t, a_t) \right], \quad \quad (1)\]
여기서 $\tau \sim \tilde{\pi}$는 $\tau = (s_0, a_0, s_1, a_1, \cdots)$인데 $s_0 \sim \rho_0$ 이며 $a_t \sim \tilde{\pi}(a_t | s_t)$이다. $\eta(\tilde{\pi})$는 $\eta({\pi})$ 더하기 $\tilde{\pi}$로 trajectory를 만들 때 만들어지는 정책 $\pi$의 advantage 함수값의 기댓값이다. 내 언어로 정리하자면,
- 현재 주어진 정책 $\pi$ 에 대해서 우리는 $\eta({\pi})$와 $A_{\pi}$를 알고 있는 상황이다.
- 우리는 다른 정책 $\tilde{\pi}$ 의 $\eta(\tilde{\pi})$를 직접 계산하지 않고 $\eta({\pi})$와 $A_{\pi}$를 사용하여 계산할 것이다.
- $\eta(\tilde{\pi})$은 $\eta({\pi})$에서 $\pi$ 대신 $\tilde{\pi}$로 trajectory를 뽑았을 때 얻게 되는 이익의 기댓값을 더해준 값이다.
- 참고로 $\pi$로 행동을 뽑았을 때 $\mathbb{E}_{a_t \sim \pi(a_t | s_t)} \left[ A_{\pi}(s_t, a_t) \right]=0$ 인 것을 생각하면 , $\mathbb{E}_{a_t \sim \tilde{\pi}(a_t | s_t)} \left[ A_{\pi}(s_t, a_t) \right]$가 $\tilde{\pi}$ 를 사용했을 때 얻게 되는 추가 이득인 것을 받아들이기 쉽다.
여전히 받아들이기 어려운 포인트가 있을 수 있다. 때로는 직관적인 설명보다 식으로 직접 증명하는게 이해에 도움을 줄 수 있다. \[\begin{matrix} \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t} A_{\pi}(s_t, a_t) \right] & = & \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t} \left(Q_{\pi}(s_t, a_t) - V_{\pi}(s_t)\right) \right] & \quad (a) \\ & = & \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t} \left(r(s_t) + \gamma V_{\pi}(s_{t+1}) - V_{\pi}(s_t)\right) \right] & \quad (b) \\ & = & \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t}r(s_t) \right] - \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ V_{\pi}(s_0) \right] & \quad (c) \\ & = & \eta(\tilde{\pi}) - \eta(\pi) & \quad (d) \end{matrix}\]
우선 $(a)$ 는 advantange 함수의 정의 $A_{\pi}(s_t, a_t) = Q_{\pi}(s_t, a_t) - V_{\pi}(s_t)$를 대입한 것이다. 다음으로 $(b)$ 는 행동가치함수에 대한 다음 벨만방정식을 대입한 것이다. \[Q_{\pi}(s_t, a_t) = r(s_t) + \gamma\mathbb{E}_{s_{t+1}\sim P(s_{t+1}|s_t, a_t)}\left[ V_{\pi}(s_{t+1})\right]\]
위를 대입하면 기댓값 안에서 기댓값이 등장하는데, Law of total expectation에 의해 기댓값 안의 값은 지워질 수 있다. Law of total expectation는 기댓값 안의 기댓값은 더 이상 확률 변수가 아니기 때문에 가능한 일이다. 내부 기댓값을 계산하는데 확률 변수가 소진되어 버린다랄까?
식 $(c)$ 는 시그마를 전개한 것이다. $r(s_t)$ 들을 다 모아놓아서 $\mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t}r(s_t) \right]$ 가 되고, 나머지는 $V_{\pi}(s_0)$만 제외하고 다 소거된다. 마지막으로 식 $(d)$ 의 첫 번째 텀은 $\eta$ 함수의 정의에 의한 것이다. 식 $(c)$ 의 두 번째 기댓값 안에서 확률 변수는 $s_0$ 밖에 없다. 따라서 $\tau \sim \tilde{\pi}$ 에서 나머지 확률변수는 사용되지 않고 $s_0$ 만 기댓값 계산에 관여할 수 있다. $s_0$는 정책과 상관 없이 $\rho_0$ 에만 결정된다. 즉, 정책 $\pi$의 초기 상태의 상태가치함수의 기댓값 즉, $\eta(\pi)$이다. 식 $(d)$ 를 정리하면 식 $(1)$이 나오게 된다 $\Box$.
식 $(1)$에 대한 근사
여전히 풀리지 않는 미스테리. 정책 $\tilde{\pi}$ 의 $\eta(\tilde{\pi})$를 직접 계산하지 않고 $\eta({\pi})$와 $A_{\pi}$를 사용하여 계산하고 싶은데, 저 기댓값의 $\tau \sim \tilde{\pi}$ 이걸 하기 위해서는 일단 정책이 좋든 나쁘든 trajectory를 만들어봐야 한다. 굉장히 비효율적이다. 우리는 $\tilde{\pi}$를 직접 시행해보지 않고도 $\eta(\tilde{\pi})$를 계산하고 싶다.
Conservative policy improvement (CPI) 논문에서는 식 $(1)$을 직접 구하는 것을 포기했다. 대신에 식 $(1)$을 근사할 수 있는 방법과 근사했을 때 발생하는 에러의 lower bound를 제시하였다. 들어가기에 앞서 한 가지 표기를 더 정의하고 가자. 정책 $\pi$를 따랐을 때 상태 $s$에 있을 확률 분포의 discounted 버전으로 생각하면 된다. 책에서는 unnormalized discounted visitations frequencies 라고 명명하였다. Rho sub pi (뤄 서브 파이) $\rho_{\pi}: \mathcal{S} \rightarrow \mathbb{R}$는 다음과 같이 정의된다. \[\rho_{\pi}(s) = P(s_0=s) + \gamma P(s_1=s) + \gamma^{2} P(s_2=s) +\cdots, \quad \quad (*)\]
이때 $s_0 \sim \rho_0$이고, 나머지는 정책 $\pi$를 따랐을 때 상태 $s$에 도착할 확률이다. 해석하자면, 각 시점에서 상태 $s$에 있을 확률에 할인률을 적용해준 것이다. $\gamma$가 1이라면 stationary distribution 느낌이 나기도 한다. 엄밀히 말하면 모든 $s$에 대해서 $\rho_\pi(s)$를 더했을 때 1이 넘을 수 있기 때문에 확률분포가 될 수 없다. 그래서 “unnormalized”, “visitation frequency”라고 부르는 것이다. 참고로 우변에 $\frac{1}{1-\gamma}$를 곱해주면 확률분포가 될 수 있다. Stationary distribution도 아닌 식 $(*)$를 사용하는 이유는 그냥 나중에 사용되기 때문이다. 비중은 낮으니 혼란스러우면 받아들이고 넘어가자!
다음으로 문제가 되는 식 $(1)$을 기댓값의 정의를 사용하여 다시 적어보자. 표기의 편의성을 위해 이산 상태/행동 공간을 가정하여 시그마 표기를 사용하였지만, 연속 공간의 경우 인테그랄 표기를 사용해도 똑같은 결과를 얻게된다. \[\begin{matrix} \eta(\tilde{\pi}) & = & \eta(\pi) + \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum\limits_{t=0}^{\infty} \gamma^{t} A_{\pi}(s_t, a_t) \right] & \quad (a) \\ & = & \eta(\pi) + \sum\limits_{t}^{\infty}\sum\limits_{s}P(s_t=s | \tilde{\pi})\sum\limits_{a}\tilde{\pi}(a | s)\gamma^{t} A_{\pi}(s, a) & \quad (b) \\ & = & \eta(\pi) + \sum\limits_{s}\sum\limits_{t=0}^{\infty}\gamma^t P(s_t=s | \tilde{\pi})\sum\limits_{a}\tilde{\pi}(a|s) A_{\pi}(s, a) & \quad (c) \\ & = & \eta(\pi) + \sum\limits_{s}\rho_{\tilde{\pi}}(s)\sum\limits_{a}\tilde{\pi}(a|s) A_{\pi}(s, a). & \quad(d) \end{matrix}, \quad \quad (2)\]
식 $(a)$는 식 $(1)$을 그대로 가져온 것이다. 식 $(b)$은 기댓값의 정의를 사용한 것이다. 굳이 디테일하게 설명하자면 먼저 기댓값의 선형성을 이용하여 $\sum\limits_{t=0}^{\infty}$를 기댓값 바깥으로 빼준 것이고, 각 시점 $t$에서 상태 $s$일 확률과 행동 $a$일 확률을 고려해서 $\gamma^{t} A_{\pi}(s, a)$의 기댓값을 계산하는 것이다. 식 $(c)$는 시그마의 순서와 $\gamma^{t}$의 순서를 바꿔준 것이다. 식 $(d)$는 식 $(*)$를 대입해준 것이다.
우리의 걱정은 정책이 좋든 나쁘든 $\tau \sim \tilde{\pi}$를 해야 한다는 것이었다. 하지만 식 $(2)$을 보니 어떤 부분이 문제인지 조금 더 잘 보인다. 정책 $\tilde{\pi}$을 포함하고 있는 부분은 $\rho(\tilde{\pi})$와 $\tilde{\pi}(a|s)$이다. 사실 $\tilde{\pi}(a|s)$는 큰 문제가 되지 않는다. 정책을 매개변수화된 함수로 모델링하면 $\tilde{\pi}(a|s)$는 쉽게 계산할 수 있기 때문이다. 하지만 $\rho(\tilde{\pi})$를 계산하는 것을 불가능에 가깝다. 따라서 CPI 논문에서는 $\rho(\tilde{\pi})$ 대신 $\rho(\pi)$를 사용하여 식 $(1)$을 근사하게 된다. 즉, \[\eta(\tilde{\pi})\approx L_{\pi}(\tilde{\pi}) :=\eta(\pi) + \sum\limits_{s}\rho_{\pi}(s)\sum\limits_{a}\tilde{\pi}(a|s) A_{\pi}(s, a). \quad \quad (3)\]
참고로 $L_{\pi}(\pi)$는 advantage function의 기댓값인 0이 되기 때문에 $\eta(\pi)$이다. 본인의 성능을 본인의 성능으로 표현해야 하니 당연이 같을 수 밖에 없긴 하다. 비록 식 $(1)$에 대한 approximation 이지만 최소한의 성질은 만족한다는 것이다. 만약 우리가 매개변수화된 정책 $\pi_\theta$를 사용한다면 매개변수가 $\theta_0$일 때 다음이 성립한다는 것이다. \[\begin{matrix} L_{\pi_{\theta_0}}(\pi_{\theta _0}) & = & \eta(\pi_{\theta_0}), \; \text{ so that} & \\ \nabla_{\theta}L_{\pi_{\theta_0}}(\pi_{\theta})|_{\theta=\theta_0} & = & \nabla_{\theta}\eta(\pi_\theta)|_{\theta=\theta_0} . & \quad (4) \end{matrix}\]
너무나도 당연한 이야기이다. 식 $(4)$에서 생각해볼 수 있는 것은 $\pi_{\theta_0}$에서 업데이트를 아주 조금만 해서 $\tilde{\pi}$를 만들어냈을 때, approximation인 $L_{\pi_{\theta}}$를 개선하면 곧 실제 $\eta$가 개선될 수 있다는 것이다. 하지만 정책 업데이트를 얼마나 조금 해야 하는지에 대한 기준이 없다.
정책이 아주 조금 변할 때, $\eta$와 $L$의 차이의 lower bound
CPI 논문에서는 정책이 아주 조금 바뀌도록 상황에서 $\eta(\tilde{\pi})$와 $L_{\pi}(\tilde{\pi})$의 차이의 lower bound를 찾아냈다. “정책이 아주 조금 바뀌는 상황”을 위해 CPI 논문에서는 다음 mixture policy를 고려하게 된다. \[\pi_{\text{new}}(a|s) = (1-\alpha)\pi_{\text{old}}(a|s) + \alpha\pi'(a|s), \quad \quad (5)\]
이때, $0\le \alpha \le 1$ 이고 $\pi’ = \operatorname{argmax}_{\pi’}L_{\pi_{\text{old}}}(\pi’)$이다. 어떻게 구하는지는 모르지만 구했다고 생각하고 설명을 계속하도록 하겠다. 기본적으로 우리의 믿음은 $L_{\pi_{\text{old}}}(\pi’)$이 큰 $\eta(\pi’)$도 클 것이라는 것이고, 사실 이 믿음은 에서 업데이트 크기가 작을수록 더 신뢰도가 올라가기 때문에 $\pi_{\text{old}}$와 $\pi’$를 섞어서 $\pi_{\text{new}}$를 만드는 것이다.
이런 $\pi_{\text{new}}$에 대해서 실제 $\eta(\pi_{\text{new}})$와 근사치 $L_{\pi_{\text{old}}}(\pi_{\text{new}})$의 관계는 다음과 같다. \[\begin{matrix} \eta(\pi_{\text{new}}) \ge L_{\pi_{\text{old}}}(\pi_{\text{new}}) - \frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2, \; \text{where} \\ \epsilon = \max\limits_{s}\left|\mathbb{E}_{a \sim \pi'(a|s)} \left[ A_{\pi_{\text{new}}}(s,a)\right] \right|. \quad\quad(6) \end{matrix}\]
부등식의 우변에서 $\frac{2\gamma}{(1-\gamma)^2}\alpha^2$은 상수이기 때문에 $\epsilon$만 살펴보자. Advantage 함수의 기댓값은 0이라는 것을 염두하면, $\pi’$가 $\pi_{\text{new}}$와 다르면 다를수록 $\epsilon$이 커지게 된다. 따라서 $\pi’$와 $\pi_{\text{new}}$가 비슷하면 $\frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2$이 0에 가까워지고, $\pi’ = \pi_{\text{new}}$이면 식 $(4)$에서 봤던 것처럼 등호가 성립하게 된다. 식 $(6)$ 부등식 증명이 생각보다 어렵지 않다. 다만, 분량을 고려해서 이 글에서 증명은 생략하거나, 나의 힘이 남아있다면 글의 마지막 부분에 남겨놓도록 하겠다.
식 $(6)$에서 얻어가야할 가장 큰 인사이트는 다음과 같다.
- 현재 정책 $\pi_{\text{old}}$에 대해서 정책 업데이트가 없는 경우 부등식 $(6)$의 등호가 성립한다. 즉,
- $\pi_{\text{new}} = \pi_{\text{old}}$일 때보다 더 높은 $L_{\pi_{\text{old}}}(\pi_{\text{new}}) - \frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2$를 갖는 $\pi_{\text{new}}$를 찾아낸다는 것의 의미는
- $\eta(\pi_{\text{new}})$가 $\eta(\pi_{\text{old}})$보다 더 높은 lower bound를 갖기 때문에 더 성능이 좋다는 것이다.
따라서 lower bound인 $L_{\pi_{\text{old}}}(\pi_{\text{new}}) - \frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2$를 커지는 방향으로 정책을 업데이트할 경우 monotonic improvement가 된다는 것이다.
여기까지가 논문의 사전지식 (preliminaries)에 해당하는 부분이다. 정리하자면,
- 한 정책의 성능을 다른 정책으로 표현하기 → 식 $(1)$
- 식 $(1)$을 근사하는 방법과 근사 오차의 lower bound → 식 $(3), (6)$
- 현재 정책보다 더 높은 lower bound를 갖는 정책을 찾으면 실제 성능지표 $\eta$도 증가하기 때문에 monotonic improvement가 보장된다.
TRPO 논문을 이해하기 위해서는 위의 과정을 이해하는 것이 가장 핵심적인 것 같다. 위 과정만 이해하고 있다면, TRPO가 CPI의 어떤 부분을 어떻게 개선을 하는지가 잘 보이게 된다.
보다 일반적인 정책으로의 확장
이제부터 TRPO 논문의 contribution에 해당하는 부분이다. 하지만 아직 TRPO 내용은 아니다. CPI를 먼저 일반적인 정책 업데이트에 사용할 수 있도록 이론적인 개선을 하고, 그 개선체의 구현 버전이 바로 TRPO이다.
CPI의 가장 큰 문제점은 식 $(5)$와 같은 mixture policy에 대해서 이론이 기술되었다는 점이다. 하지만 많은 곳에서 mixture policy를 거의 사용하지 않는다. TRPO 논문에서는 식 $(6)$의 결론을 일반적인 stochastic policy에 대해서 확장하였다.
우리는 식 $(6)$의 lower bound를 증가시키지만, 그렇다고 이전 정책과는 너무 달라지지 않게 하기 위하여 mixture policy를 사용하였다. 여기서 어떤 점을 개선할 수 있을까? Lower bound는 증가시키는 것은 동일하되, 이전 정책과 가까운 정책을 어떻게 정의할 것인지를 바꿔볼 수 있을 것이다. 따라서 TRPO 논문에서는 정책과 정책 사이의 거리를 측정하기 위하여 the total variation divergence (TV)를 사용하였다. 두 확률분포 $p$와 $q$의 TV는 다음과 같이 정의된다. \[D_{\text{TV}}(p \Vert q) = \frac{1}{2}\sum_i |p_i - q_i|.\]
위는 임의의 확률분포 $p$와 $q$의 TV 거리이다. TRPO에서는 두 정책 사이의 TV 거리를 다음과 같이 정의했다. \[D_{\text{TV}}^{\text{max}}(\pi, \tilde{\pi})=\max\limits_{s}D_{\text{TV}}(\pi(\cdot | s) \Vert \tilde{\pi}(\cdot | s)). \quad \quad (7)\]
각 상태 $s$에서 계산한 두 정책의 TV 거리 중에서 가장 큰 값을 두 정책의 TV 거리라고 정의한 것이다. TRPO 논문에서는 $\alpha = D_{\text{TV}}^{\text{max}}(\pi, \tilde{\pi})$로 설정할 경우 다음과 같은 부등식이 성립함을 보였다. \[\eta(\pi_{\text{new}}) \ge L_{\pi_{\text{old}}}(\pi_{\text{new}}) - \frac{4\epsilon\gamma}{(1-\gamma)^2}\alpha^2, \; {\text{ where }} \;\epsilon = \max\limits_{s, a} |A_{\pi}(s, a)|. \quad \quad (8)\]
현재 정책 $\pi_{\text{old}}$와 TV 거리 $\alpha$만큼 떨어진 정책들에 대해서 식 $(8)$의 부등식이 성립한다는 것이다. 그렇다면 CPI와 같은 논리를 적용해보자. 현재 정책보다 lower bound가 높으면서, 현재 정책과 TV 거리가 $\alpha$만큼 떨어진 정책을 찾으면 그 정책은 monotonically improved된 정책이 된다는 것이다. 따라서, parameterized policy를 사용할 경우, lower bound의 gradient를 계산한 후, 그 방향으로 line search하면서 TV 거리가 $\alpha$인 정책을 찾으면 되는 것이다.
하지만 우리는 TV 거리보다 KL 거리가 더 익숙하다. 따라서 TRPO 논문에서는 다음의 TV 거리와 KL 거리의 관계식을 사용하였다. \[D_{\text{TV}}(p \Vert q)^2 \le D_{\text{KL}}(p \Vert q)\]
TV 거리와 마찬가지로 두 정책 사이의 KL 거리를 다음과 같이 정의하자. \[D_{\text{KL}}^{\text{max}}(\pi, \tilde{\pi})=\max\limits_{s}D_{\text{KL}}(\pi(\cdot | s) \Vert \tilde{\pi}(\cdot | s)).\]
TV 거리의 제곱보다 KL 거리의 값이 더 크기 때문에 식 $(8)$의 $\alpha^2$을 KL 거리로 바꿔줘도 부등식이 성립한다. 즉, \[\eta(\tilde{\pi}) \ge L_{\pi}(\tilde{\pi}) - C D_{\text{KL}}^{\text{max}}(\pi, \tilde{\pi}), \; {\text{ where }} C=\frac{4\epsilon\gamma}{(1-\gamma)^2}. \quad \quad (9)\]
이 식 $(9)$가 TRPO 논문의 핵심 이론이라고 할 수 있다. 이 부등식을 이용하여 정책을 업데이트하는 알고리즘은 다음 그림과 같다.

Lower bound를 최대화하면서 정책을 찾는 알고리즘이다. Lower bound를 Minorization라고 부르기도 하는 것 같다. 그래서 위 알고리즘을 Minorization-Maximization (MM) 알고리즘이라고 부른다. MM 알고리즘 분야에서 실제 성능지표 $\eta$ 대신으로 최적화되는 대상을 surrogate function이라고 부른다. 따라서 lower bound를 surrogate function이라고 부른다.
Trust Region Policy Optimization
지금까지는 이론적인 설명이었다. 하지만 이론과 구현 사이에는 괴리가 있는 법이다. 먼저 지금까지 이론 전개에서 우리는 정책의 advantage function을 정확히 안다고 가정했다. 그리고 surrogate function을 최적화 할 수 있다고 가정했다. Surrogate function 안에는 KL 거리가 있다. KL 거리가 $\alpha$인 정책을 어떻게 찾을 수 있을까? 지금까지 이론을 바탕으로 이론을 근사하면서 구현한 버전이 TRPO라고 생각하면 좋을 것 같다.
실제 구현에서는 대부분 function approximation을 사용하기 때문에 매개변수화된 정책을 찾는 상황을 생각하자. 그리고 앞으로 다음과 같이 표기를 단순히 할 것이다.
- $\eta(\theta) := \eta(\pi_{\theta})$
- $L_{\theta}(\tilde{\theta}):=L_{\pi_{\theta}}(\pi_{\tilde{\theta}})$
- $D_{\text{KL}}(\theta \Vert \tilde{\theta}) = D_{\text{KL}}(\pi_\theta \Vert \pi_{\tilde{\theta}})$
식 $(9)$의 lower bound를 최대화하기 위해서는, 첫 번째 텀 $L_{\pi}(\tilde{\pi})$은 최대한 크게, 두 번째 텀 $C D_{\text{KL}}^{\text{max}}(\pi, \tilde{\pi})$은 최대한 작게 만들어주면 된다 (두 번째 텀은 항상 양수이기 때문이다). 한편, 두 번째 텀은 $\epsilon$과 KL 거리를 포함하고 있다. $\epsilon$과 KL 거리가 작으면 작을수록 두 번째 텀이 최소가 된다. $\epsilon$과 KL 거리를 최소화시키는 것은 쉽지 않을 것이다. 하지만 현재 정책과 KL 거리가 작은 정책을 찾는 것은 비교적 쉬울 것이다. 따라서 TRPO에서는 다음과 같이 최적화 문제를 변형해서 사용한다. \[\begin{matrix} \operatorname*{maximize}\limits_{\theta}L_{\theta_{\text{old}}}(\theta) \\ \text{subject to } \; D_{\text{KL}}^{\text{max}}(\theta_{\text{old}}, \theta)\le \delta. \end{matrix} \quad \quad (11)\]
$D_{\text{KL}}^{\text{max}}(\theta_{\text{old}}, \theta)\le \delta$인 $\theta$ 들중에 $L_{\theta_{\text{old}}}(\theta)$를 가장 크게 만들어주는 $\theta$를 찾는 constrained optimization을 푸는 것이다. 하지만 $D_{\text{KL}}^{\text{max}}$은 계산하기 나쁘다. 모든 상태 $s$에 대해서 KL 거리를 계산해야 되기 때문이다. 따라서 한 번 더 단순화하여 평균 KL 거리를 사용하게 된다. \[\overline{D}^{\rho}_{\text{KL}}(\theta_1, \theta_2)=\mathbb{E}_{s \sim \rho} \left[ D_{\text{KL}}(\pi_{\theta_1}(\cdot | s) \Vert \pi_{\theta_2}(\cdot | s))\right].\]
Max 대신 기댓값을 사용하면 좋은 점은 실제 기댓값을 계산하는 대신 경험 데이터로부터 표본평균 구해서 근사할 수 있다는 점이다. 따라서 새로운 최적화 식은 다음과 같다. \[\begin{matrix} \operatorname*{maximize}\limits_{\theta}L_{\theta_{\text{old}}}(\theta) \\ \text{subject to } \; \overline{D}^{\rho}_{\text{KL}}(\theta_{\text{old}}, \theta)\le \delta. \end{matrix} \quad \quad (12)\]
Sample-based Estimation of the Objective and Constraint
열심히 달려왔지만, 식 $(12)$를 여전히 구현하기 어려울 것 같다. 이번 섹션에서는 TRPO가 실제 구현을 위해 식 $(12)$를 어떻게 바꾸는지에 대해 이야기해볼 것이다. 먼저 식 $(3)$을 가져와서 식 $(12)$에 대입해보자 \[\begin{matrix} \operatorname*{maximize}\limits_{\theta}\sum\limits_{s}\rho_{\theta_{\text{old}}}(s)\sum\limits_{a}\pi_{\theta}(a|s) A_{\theta_{\text{old}}}(s, a). \\ \text{subject to } \; \overline{D}^{\rho}_{\text{KL}}(\theta_{\text{old}}, \theta)\le \delta. \end{matrix} \quad \quad (13)\]
실제 구현에서는 최적화 대상을 직접 계산 어렵기 때문에 데이터로부터 추정을 하는 방식을 많이 택한다. $\sum\limits_{s}\rho_{\theta_{\text{old}}}(s)$는 실제 구현에서는 $\pi_{\theta_{\text{old}}}$ 따라서 에피소드를 진행하여 $s$를 얻는 방식으로 진행된다. 즉, $\mathbb{E}_{s \sim \rho_{\theta_{old}}}[\cdots]$이 된다.
다음으로 $\sum\limits_{a}\pi_{\theta}(a|s) A_{\theta_{\text{old}}}(s, a)$ 부분이다. 먼저 $A_{\theta_{\text{old}}}$ 대신 $Q_{\theta_{\text{old}}}$를 사용했다고 한다. 이유는 따로 나와있지 않지만, on-policy 알고리즘들에서 $Q$ 함수를 추정하는 다양한 방식들이 있기 때문이다. 예를 들면 REINFORCE에서는 return $G_t$를 $Q$ 함수의 추정값으로 사용한다. 반면, advantage function을 사용하기 위해서는 상태가치함수를 모델링해줘야 하기 때문에 행동가치함수로 바꿔준 것 같다.
다음으로 $\sum\limits_{a}\pi_{\theta}(a|s)$을 위해서는 importance sampling을 해줬다고 한다. 행동공간이 굉장히 크거나 연속적이면 모든 $a$에 대해서 summation을 해주기 어려울 것이다. 따라서, 우리가 갖고 있는 데이터로부터 계산을 해줘야할텐데, 우리가 갖고 있는 데이터는 $\pi_{\theta_{\text{old}}}$ 또는 이전 정책들로부터 만들어진 것이다. 이런 데이터 편향을 고려해줄 수 있는 방법이 importance sampling이다.
위 세 문단을 반영하여 TRPO의 최적화식을 적어보면 다음과 같다. \[\begin{matrix} \operatorname*{maximize}\limits_{\theta}\mathbb{E}_{s\sim\rho_{\theta_{\text{old}}}, a \sim q} \left[ \frac{\pi_{\theta}(a|s)}{q(a|s)} Q_{\theta_{\text{old}}}(s, a) \right]. \\ \text{subject to } \; \mathbb{E}_{s\sim\rho_{\theta_{\text{old}}}}\left[D_{\text{KL}}\left( \pi_{\theta_{\text{old}}}(\cdot|s) \Vert \pi_{\theta}(\cdot|s) \right) \right] \le \delta. \end{matrix} \quad \quad (14)\]
이때, $q$는 importance sampling을 할 때, 데이터를 뽑는 정책이며 현재 정책이라고 생각하면 된다. 여전히 기댓값으로 나와 있어서 어려워보인다. 하지만 기댓값은 현재 정책으로 환경과 상호작용하여 경험 데이터를 얻고, 이를 대입하여 표본평균을 계산하여 추정하게 된다.
식 $(14)$가 TRPO의 최종 최적화식이다. 논문의 본문과 부록에서 sampling 방법론과 최적화 알고리즘을 푸는 방법에 대해서 소개하고 있다. 하지만 구현을 진짜 해보고 싶은 것이 아니라면 굳이 알 필요는 없는 것 같다.
나도 이걸 어떻게 구현해야 할까 생각이 들어서 TRPO 구현체들을 찾아보았는데 정말 깜짝 놀랄 일이 있었다. 생각보다 TRPO 구현체가 없는 것이었다. 노승은님의 minimal RL와 같이 공부를 위한 레포지토리에도 없을 뿐만 아니라, Stable baseline3이나 카카오 엔터프라이즈의 JORLDY와 같이 큰 레포지토리에도 TRPO 구현을 찾아볼 수 없었다. 정말 구현이 어려운 논문이구나라는 것을 직감하고 나는 논문의 내용을 이해하는 것에 만족했다.
Experiments
Cart Pole, Swimmer, Walker, Hopper에 대한 실험 결과 그래프이다. 여기서 Vine (파란색 실선)과 Single Path (초록색 실선)이 TRPO 알고리즘을 나타낸다. 참고로 vine과 single path는 논문에서 제안하는 샘플링 기법이다. Single path가 흔히 아는 우리가 사용하는 방법으로서, 환경과 하나의 에피소드 동안 상호작용하는 것을 의미한다.
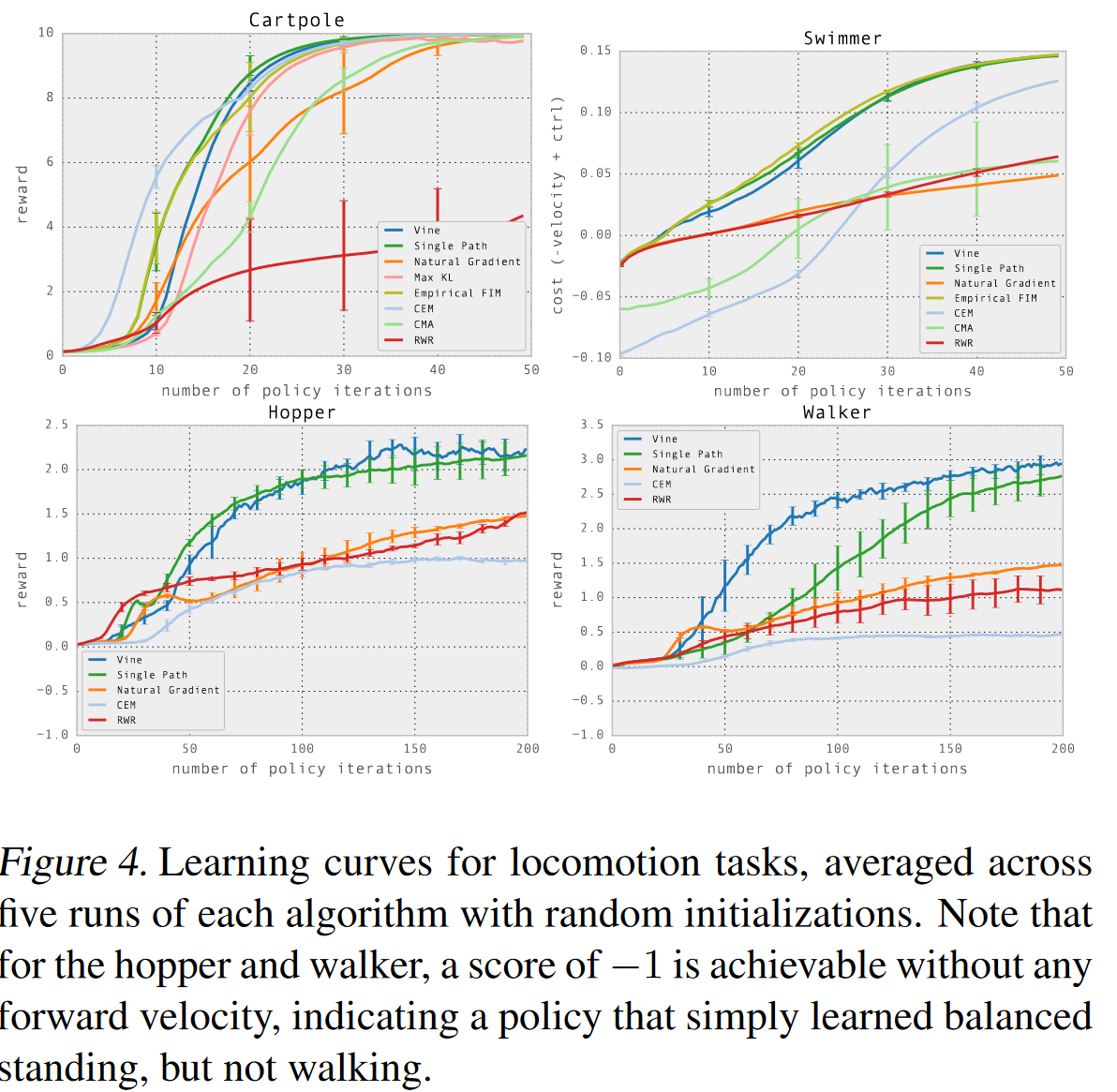
Atari에 대한 실험 결과는 다음과 같다.
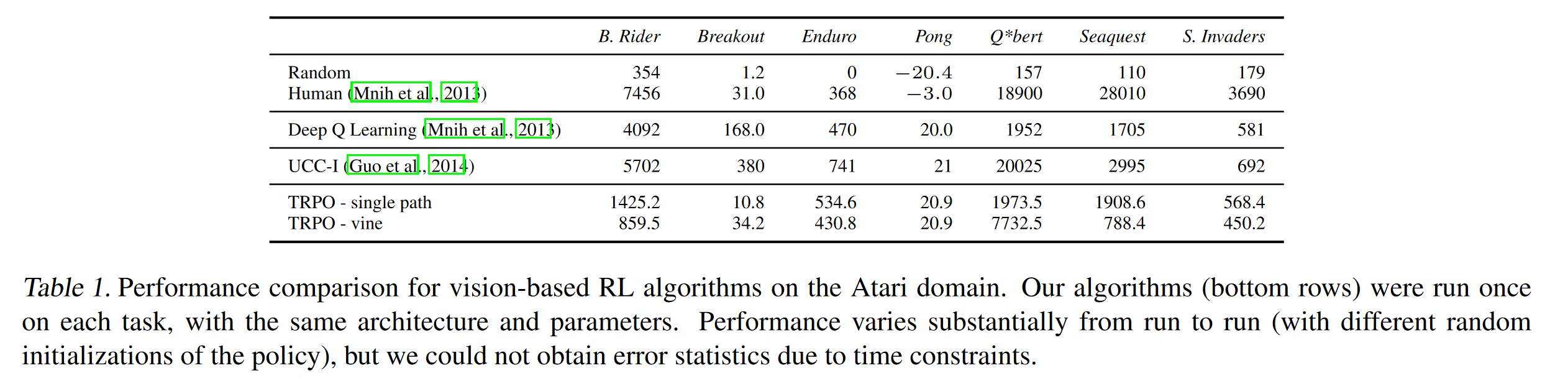
마무리 멘트
읽어야지 읽어야지만 생각하고 절대 안 읽은 논문을 이제야 읽었다. 다 읽고 나니 묵은 때가 싸악 내려가는 것 같다. 그리고 내가 이 난이도 높은 논문을 읽은게 믿겨지지 않으며 많이 성장했다는 것을 느낀다. 앞으로 몇 주 동안은 논문보다는 강화학습 코딩을 하는데 시간을 할애해야 겠다.
참고문헌
[1] Schulman, John, Sergey Levine, Pieter Abbeel, Michael Jordan, and Philipp Moritz. “Trust Region Policy Optimization.” In Proceedings of the 32nd International Conference on Machine Learning, edited by Francis Bach and David Blei, 37:1889–97. Proceedings of Machine Learning Research. Lille, France: PMLR, 2015. https://proceedings.mlr.press/v37/schulman15.html.

