3차원 원 적합(3d-circle fitting)

    3차원 좌표공간에 원 모양의 데이터들이 주어졌을 때, 이 데이터에 가장 잘 맞는 원의 방정식은 어떻게 구할 수 있을까요?
    만약 주어진 데이터들이 정확하게 한 원 위에 있다는 것을 안다면 단순하게 연립방정식을 푸는 것에 지나지 않을 것입니다.
    하지만 현실 세계의 데이터는 관측 오차 등의 노이즈를 포함하고 있기 때문에 주어진 데이터들이 모두 한 원 위에 있기는 쉽지 않습니다.
    그렇다면 우리는 현실과 타협하여 주어진 데이터들을 가장 잘 대표할 수 있는 원의 구하는 것으로 목표를 바꿔야할 것입니다.
    이번 포스트에서는 3차원 좌표공간에 주어진 데이터들에 가장 적합한 원의 방정식을 찾는 것을 다뤄보도록 하겠습니다.

    들어가기에 앞서 이 포스트는 참고문헌 1 을 참고하여 재구성한 포스트임을 미리 말씀드립니다.
    (This post is a reproducing of the reference 1 in Korean. Some contents was added as needed )

포스트 소개

    이번 포스트에서는 3차원 좌표 공간에 주어진 데이터들로부터 가장 적합한 원을 찾는 방법을 다룰 예정입니다. 다양한 방법이 있지만 우리는 다음 과정을 통해 가장 적합한 원을 찾아보도록 하겟습니다.

1. 특이값분해(Singular value decomposition, SVD)를 통해 주어진 데이터에 가장 적합한 평면을 찾는다.
2. 찾은 평면과 $xy$ 평면 사이의 각 $\theta$ 를 구해서 모든 데이터들을 $\theta$ 만큼 회전시켜주고 $xy$ 평면에 투영시킨다.
3. 지난 포스트에서 다룬 2차원 원 적합을 적용하여 원의 중심과 반지름을 구해준다.
4. 구한 원의 중심을 원래의 축 체계로 변환시킨다.

3차원 좌표공간에 있는 원의 방정식

    2차원 좌표평면에 있는 원의 방정식을 $<rcos\theta,rsin\theta> + <x_0,y_0>$와 같이 매개변수 방정식으로 나타낼 수 있는 것처럼, 3차원 좌표공간에 있는 원의 방정식 또한 다음과 같이 나타낼 수 있습니다.

$\mathbf{P}_{\textbf{circle}}(\theta) = rcos\theta\mathbf{u} + rsin\theta(\mathbf{n}\times\mathbf{u})+\mathbf{C},\;0\le t \le 2\pi$

    이 때, 원의 반지름은 $r$, 원의 중심은 $\mathbf{C}=(x_0,y_0,z_0)$, 단위법선벡터는 $\mathbf{n}$이며, $\mathbf{u}$는 $\mathbf{n}$과 수직한 아무 벡터일 수 있습니다.

    위 매개변수 방정식은 2차원 좌표평면에 있는 원의 방정식과 비교하여 생각해보면 쉽게 이해할 수 있습니다. 먼저 2차원 좌표평면에 있는 원의 방정식을 다시 적어보면 다음과 같습니다.

$rcos\theta<1, 0> + rsin\theta <0, 1> + <x_0, y_0>$

    이 때, $<1, 0>$는 $x$축을 나타내는 단위방향벡터이며 $<0, 1>$는 $y$축을 나타내는 단위방향벡터입니다. 이를 확장하여 $xy$ 평면 위에 있는 원을 3차원 좌표 공간에 나타내보겠습니다.

$rcos\theta<1, 0, 0> + rsin\theta <0, 1, 0> + <x_0, y_0, 0>$

    3차원 좌표공간에서 $xy$ 평면의 법선벡터($\mathbf{n}$)는 $<0,0,1>$ 입니다. $x$축을 나타내는 방향벡터 $<1, 0, 0>$는 $\mathbf{n}$과 수직한 벡터입니다($\mathbf{u}$). 마지막으로 $y$축을 나타내는 방향벡터 $<0, 1, 0>$ 는 $\mathbf{n}$과 $\mathbf{u}$에 동시에 수직하는 벡터입니다 ($\mathbf{n}\times\mathbf{u}$).

    이를 유념하면서 다시 3차원 원의 방정식을 보면 단순히 원이 이루는 평면의 법선벡터를 이용해서 새로운 축 $\mathbf{u}$과 $(\mathbf{n}\times\mathbf{u})$를 만들어서 표현한 것에 지나지 않는다는 것을 알 수 있습니다.

    지금까지 3차원 좌표공간에 있는 원의 방정식을 표현하는 방법을 알아보았습니다. 우리는 나중에 이 방정식을 통해 데이터 포인트를 샘플링을 할 것입니다.

특이값분해를 이용한 평면 적합

    우리에게 $n$개의 데이터가 주어졌다고 가정해봅시다. : $\mathbf{P}_1,\; \mathbf{P}_2,\; \cdots,\; \mathbf{P}_n\;\; \text{where}\;\; \mathbf{P}_i = (x_i, y_i, z_i)^T$. 우리는 이 데이터에 가장 적합한 평면을 찾는 것이 목표입니다. 가장 적합한 평면을 찾기 위해서 우리는 각각의 데이터와 평면 사이의 수직 거리를 구하고 이를 제곱하여 합하는 최소제곱법을 사용할 것입니다.

    먼저 데이터 포인트들을 하나의 $n\times3$ 행렬 $A$로 나타낼 수 있습니다.

$A = (\mathbf{P}_0-\mathbf{c}, \mathbf{P}_1-\mathbf{c}, \cdots, \mathbf{P}_n-\mathbf{c})^T$

    이 때, 편의를 위해서 각 데이터에서 데이터의 중심 ($\mathbf{c} = \frac{1}{n}\sum_i{\mathbf{P}_i}$) 을 빼주었습니다.(이렇게 평행이동한 데이터들의 중심은 원점이 됩니다.)

    평행이동된 점($\mathbf{P}_i - \mathbf{c}$) 과 평면사이의 거리는 법선벡터와 내적의 정의를 사용하면 $(\mathbf{P}_i - \mathbf{c})^T\mathbf{n}$ 인 것을 알 수 있습니다(데이터를 평면에 수직한 법선벡터 $\mathbf{n}$ 에 투영한 것이 내적이므로). 그렇다면 $A\mathbf{n}$은 각 포인트에서 평면까지의 거리들을 나타내는 벡터가 되는 것이고. 각 포인트와 평면사이 거리의 제곱의 합은 벡터 $A\mathbf{n}$의 유클리디안 크기인 $\lVert A\mathbf{n} \rVert^2$이 될 것입니다. 우리는 $\lVert A\mathbf{n} \rVert^2$ 을 최소로 만들어주는 평면을 찾고 싶은 것이므로, 우리는 다음을 만족하는 $\mathbf{n}$을 찾아주어야 합니다.

$\mathbf{n} = \arg!\min_{\mathbf{n}\in \mathbb{R}^3 \atop |\mathbf{n}|=1} | \mathbf{A} \mathbf{n} |^2$

    이를 만족하는 $\mathbf{n}$은 특이값분해(이하 SVD)를 통해 쉽게 구할 수 있습니다. SVD에 의해서 행렬 $A$는 다음과 같이 분해될 수 있습니다.

$A = U\Sigma V^T$

    이 때, $U$는 $n \times n$ orthonormal 행렬, $V$는 $3 \times 3$ orthonormal 행렬이고 각각은 $A$의 columns space와 row space의 orthogonal basis 입니다. 그리고 $\Sigma$는 특이값 $\sigma_1 \ge \sigma_2 \ge \sigma_3 \ge 0$ 을 원소로 갖는 대각행렬입니다. SVD에 대한 더 자세한 설명은 새로운 포스트에서 다뤄보도록 하겠습니다. 참고로 SVD는 $A$와 같은 직사각행렬에 대해서도 존재합니다.

    SVD를 이용하여 $| \mathbf{A} \mathbf{n} |^2$를 다음과 같이 다시 적어볼 수 있습니다.

$\begin{matrix} | A \mathbf{n} |^2 & = & A\mathbf{n} \cdot A\mathbf{n} \\ & = & (A\mathbf{n})^TA\mathbf{n} \\ & = & (U\Sigma V^T \mathbf{n})^TU\Sigma V^T\mathbf{n} \\ & = & \mathbf{n}^T V \Sigma U^T U\Sigma V^T\mathbf{n} \\ & = & \mathbf{n}^T V \Sigma \Sigma V^T\mathbf{n} \\ & = & (\Sigma V^T \mathbf{n})^T \Sigma V^T\mathbf{n} \\ & = & \Sigma V^T \mathbf{n} \cdots \Sigma V^T\mathbf{n} \\ & = & |\Sigma V^T \mathbf{n}|^2 \\ & = & (\sigma_1 b_1)^2 + (\sigma_2 b_2)^2 + (\sigma_3 b_3)^2 \\ \end{matrix}$

    이 때, $\mathbf{b} = V^T\mathbf{n}$ 입니다. 그리고 $\sigma_3$가 가장 작기 때문에 우리는 $\mathbf{b} = (0,0,1)^T$ 를 선택해줌으로써 $| A \mathbf{n} |^2$를 최소로 만들어 줄 수 있습니다.(Lagrange 승수법과 singular value와 선형변환된 벡터 사이의 부등식을 통해 유도할 수 있습니다.)

    따라서 우리는 $|A \mathbf{n} |^2$를 최소로 만들어주는 $\mathbf{n}$을 다음과 같이 구할 수 있습니다.

$\begin{matrix} V^T \mathbf{n} & = & \mathbf{b} \\ V V^T \mathbf{n} & = & V \mathbf{b} \\ \mathbf{n} & = & V \mathbf{b} \\ & = & V \left( \begin{smallmatrix} 0\\0\\1 \end{smallmatrix} \right) \\ & = & V(:,3) \end{matrix}$

즉, 법선벡터 $\mathbf{n}$을 $V$의 세 번 째 열 벡터로 선택함으로써 우리가 찾는 평면을 찾을 수 있습니다.

지금까지 주어진 데이터로부터 가장 적합한 평면을 SVD 를 통해 찾아보았습니다. 다음 단계는 찾은 평면의 법선벡터와 $xy$ 평면 사이의 각도를 구하고 데이터들을 모두 회전시켜주고 $xy$ 평면에 투영시켜주는 단계입니다.

벡터들의 축 회전 : Rodrigues rotation

    위 단계에서 우리는 SVD를 사용하여 주어진 데이터들에 가장 적합한 평면을 찾아보았습니다. 다음으로 우리는 주어진 데이터는 잠시 잊고 평면 위에 있는 벡터를 $xy$ 평면으로 회전시키는 방법에 대해서 알아보겠습니다.이를 위해서 우리는 Rodrigues' rotation formula 를 사용할 것입니다.

    Rodrigues' rotation formula 는 주어진 벡터 $P$ 를 특정한 축을 기준으로 $\theta$만큼 축 회전한 벡터 $P_{rot}$ 를 구하는 공식입니다. 이 때 축을 나타내는 단위벡터를 $k$ 라고 하면 Rodrigues' rotation formula 는 다음과 같습니다.

$P_{rot} = P cos\theta + (\mathbf{k} \times P) sin\theta + \mathbf{k} \; (\mathbf{k} \cdot P) (1 - cos\theta)$

    Rodrigues' rotation formula 에 대해서는 다음 포스트에서 다루는 것으로 하고 일단은 받아들이고 진행하겠습니다. (유도는 어렵지 않기 때문에 궁금하신 분들께서는 참고문헌 3 을 참조시면 좋을 것 같습니다.) 우리의 경우 회전할 각 $\theta$는 구한 평면의 법선벡터 $\mathbf{n}$와 $xy$ 평면의 법선벡터 $(0,0,1)^T$ 의 각을 구하면 되고 회전 축은 그 둘의 외적을 사용하면 됩니다. $\mathbf{k} = \mathbf{n} \times (0,0,1)^T$

    주어진 데이터들을 위에서 구한 $\theta$와 $\mathbf{k}$로 Rodrigues' rotation을 해준 다음 $z$ 좌표를 0으로 만들어주면 데이터들을 $xy$ 평면으로 프로젝션 시킨 것과 같습니다. 이 때, 회전 변환은 거리 정보는 유지해준채 회전하는 것이기 때문에 원이 그대로 유지될 수 있습니다.

    지금까지 우리는 주어진 데이터들을 거리 정보는 유지한채 $xy$ 평면으로 프로젝션 시키는 방법을 알아보았습니다. 즉, 3차원 공간의 데이터들을 2차원 좌표평면에 프로젝션 시켰습니다. 우리는 이제 이전 포스트에서 알아본 2차원 원 적합 방법을 통해 원의 방정식을 구할 수 있습니다. 이렇게 구한 원의 방정식에서 원의 중심을 다시 Rodrigues' rotation formula 을 이용하여 3차원 좌표 공간으로 돌려놓으면 3차원 원 적합 문제는 해결될 수 있습니다.

    마지막으로 지금까지의 과정을 파이썬 코드를 통해 어떻게 구현될 수 있는지 알아보도록 하겠습니다.

파이썬 코드 구현

    먼저 3차원 좌표 공간에 원을 만들어보도록 하겠습니다. 3차원 좌표공간에 있는 원의 방정식 에서 알아본 원의 방정식을 이용하도록 하겠습니다. 원의 중심은 $(1,1,1)$, 반지름 $r$ 은 2이고 법선벡터( $\mathbf{n}$ )는 $(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$ 으로 설정하고 $\mathbf{n}$ 과 수직인 벡터 $\mathbf{u}$ 는 $(\frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}}, \frac{1}{\sqrt{6}})$ 로 설정하겠습니다. 쉽게 생각하면 정육면체의 모서리에 접해 있는 원이라고 생각하시면 됩니다.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 코드를 다시 실행해도 같은 노이즈를 선택하기 위해 시드를 설정합니다.
np.random.seed(1)

#----------------------------------------------------------
# 원 위의 점을 생성하는 함수
# P_circle(t) = r*cos(t)*u + r*sin(t)*(n x u) + C
#----------------------------------------------------------
def generate_circle_by_vectors(t, C, r, n, u):
    n = n / np.linalg.norm(n)
    u = u / np.linalg.norm(u)
    
    P_circle = (r * np.cos(t)[:,np.newaxis] * u) + (r * np.sin(t)[:,np.newaxis] * np.cross(n,u)) + C
    return P_circle

#----------------------------------------------------------
# 원 만들기
r = 2                     # 반지름
C = np.array([1,1,1])     # 원의 중심
n = C / np.linalg.norm(C) # 법선 벡터
u = np.array([1, -2, 1])  # 법선벡터와 수직인 벡터
u = u / np.linalg.norm(u) #

t = np.linspace(0, 2*np.pi, 100)
P_gen = generate_circle_by_vectors(t, C, r, n, u)
#----------------------------------------------------------

#----------------------------------------------------------
# 원에서 데이터 샘플링하기
#----------------------------------------------------------
t = np.linspace(-np.pi, -0.25*np.pi, 100)
P = generate_circle_by_vectors(t, C, r, n, u)

# 샘플링한 데이터에 노이즈 추가하기
P += np.random.normal(size = P.shape) * 0.1

# 원과 샘플링된 데이터를 각 평면에 투영시킨 모습을 plot
f, ax = plt.subplots(1, 3, figsize = (12,4))
alpha_pts = 0.5
i = 0
ax[i].plot(P_gen[:, 0], P_gen[:, 1], 'y-', lw = 3, label = 'Generating circle')
ax[i].scatter(P[:, 0], P[:, 1], alpha = alpha_pts, label = 'Cluster points P')
ax[i].set_title("View X-Y")
ax[i].set_xlabel('x')
ax[i].set_ylabel('y')
ax[i].set_aspect('equal', 'datalim')
ax[i].margins(.1, .1)
ax[i].grid()

i = 1
ax[i].plot(P_gen[:, 0], P_gen[:, 2], 'y-', lw = 3, label = 'Generating circle')
ax[i].scatter(P[:, 0], P[:, 2], alpha = alpha_pts, label = 'Cluster points P')
ax[i].set_title("View X-Z")
ax[i].set_xlabel('x')
ax[i].set_ylabel('z')
ax[i].set_aspect('equal', 'datalim')
ax[i].margins(.1, .1)
ax[i].grid()

i = 2
ax[i].plot(P_gen[:, 1], P_gen[:, 2], 'y-', lw = 3, label = 'Generating circle')
ax[i].scatter(P[:, 1], P[:, 2], alpha = alpha_pts, label = 'Cluster points P')
ax[i].set_title("View Y-Z")
ax[i].set_xlabel('y')
ax[i].set_ylabel('z')
ax[i].set_aspect('equal', 'datalim')
ax[i].margins(.1, .1)
ax[i].grid()

f.tight_layout()

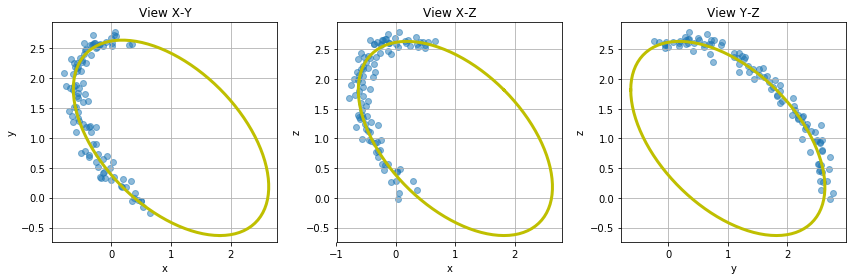
    데이터는 만들었으니 이제 원 적합을 단계별로 진행해보도록 하겠습니다. 첫 단계는 SVD를 이용한 가장 적합한 평면 찾기 단계입니다.
    우리는 먼저 1. 데이터 행렬 $P$를 만들고 2. A에서 데이터의 중심을 빼준 다음 3. $P$를 SVD를 하여 4. $V$ 행렬의 3번 째 컬럼을 적합된 평면의 법선벡터로 선택할 것입니다. 레츠고

# 1. 행렬 A 만들기, 이전 쉘에서 만든 P와 같습니다.
# 2. 데이터의 중심 구해서 빼기
P_mean = P.mean(axis = 0)
P_centered = P - P_mean

# 3. A를 SVD 하기
U, s, V = np.linalg.svd(P_centered)

# 4. 세 번 째 열을 법선벡터로 선택하기
normal = V[2, :] # np.linalg.svd 는 V 의 transpose를 반환해줍니다. 따라서 3번 째 행을 법선벡터로 선택해줍니다.
d = -np.dot(P_mean, normal)

print("The normal vector of fitted plane : ", n)
print("The groud truth normal vector : ", normal)

The normal vector of fitted plane :  [0.57735027 0.57735027 0.57735027]
The groud truth normal vector :  [-0.593907   -0.57179417 -0.56597341]

    주어진 데이터에 가장 적합한 평면의 법선벡터를 찾았습니다. 원을 만들 때 정의한 법선벡터(n_gen)과 상당히 비슷한 것을 알 수 있습니다.
    다음으로 법선벡터 $\mathbf{n}$과 $(0,0,1)^T$ 사이의 각도 $\theta$를 구하고 각 데이터들을 Rodrigues' rotation formula 사용해서 $xy$평면과 평행하게 회전하도록 하겠습니다. 각도는 “서로 다른 두 단위벡터 사이의 내적 값은 두 각이 이루는 각의 코사인 값과 같다.”를 생각하면 쉽게 구할 수 있습니다.

def rodrigues_rot(P, n0, n1):
    
    # 만약 P가 1d 행렬이라면(점들의 집합), 메트릭스로 바꿔줍니다.
    if P.ndim == 1:
        P = P[np.newaxis, :]
        
    # 회전축 벡터 k와 각도 theta 구하기
    n0 = n0 / np.linalg.norm(n0)
    n1 = n1 / np.linalg.norm(n1)
    k = np.cross(n0, n1)
    k = k / np.linalg.norm(k)
    theta = np.arccos(np.dot(n0, n1))

    # 회전된 데이터의 행렬 만들기
    P_rot = np.zeros((len(P), 3))
    for i in range(len(P)):
        P_rot[i] = (P[i]*np.cos(theta)) + (np.cross(k, P[i])*np.sin(theta)) + (k*(1-np.cos(theta))*np.dot(k, P[i]))
        
    return P_rot

P_xy = rodrigues_rot(P_centered, n, [0,0,1])

    회전한 P_xy 데이터의 $x$축, $y$축 만을 사용하여 2차원 원적합을 하도록 하겠습니다.

def circle_fitting_2d(x, y):
    A = np.array([np.ones(len(x)), x, y]).T
    b = A[:, 1] ** 2 + A[:, 2] ** 2
    c = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(b)
    
    xc = c[1] / 2
    yc = c[2] / 2
    r = np.sqrt(c[0] + xc ** 2 + yc ** 2) 
    
    return xc, yc, r

xc, yc, r = circle_fitting_2d(P_xy[:,0], P_xy[:,1])

# Fitting 된 원의 그리기
t = np.linspace(0, 2*np.pi, 100)
xx = xc + r * np.cos(t)
yy = yc + r * np.sin(t)

plt.figure(figsize = (6,6))
plt.plot(xx, yy, 'k--', lw = 2, label = 'Fitting circle')
plt.plot(xc, yc, 'k+', ms = 10)
plt.scatter(P_xy[:,0], P_xy[:,1], alpha = alpha_pts, label = 'Projected_points')
plt.legend(loc = 1)
plt.show()

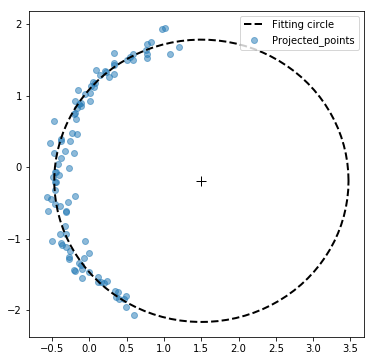
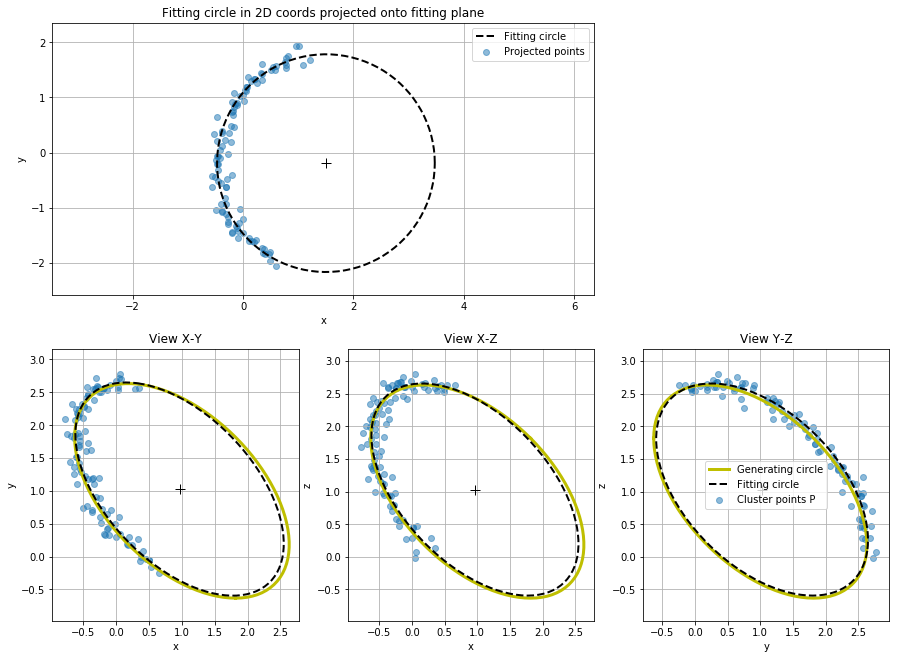
    2차원에서 적합한 원의 중심과 반지름 알았으니 다시 원래의 평면으로 보내줍시다 !

# 피팅된 원의 센터를 다시 원래 평면으로 보내기
C = rodrigues_rot(np.array([xc, yc, 0]), [0,0,1], n) + P_mean
C = C.flatten()

#-------------------------------------------------------------------------------
# Init figures
#-------------------------------------------------------------------------------
fig = plt.figure(figsize=(15,11))
alpha_pts = 0.5
figshape = (2,3)
ax = [None]*4
ax[0] = plt.subplot2grid(figshape, loc=(0,0), colspan=2)
ax[1] = plt.subplot2grid(figshape, loc=(1,0))
ax[2] = plt.subplot2grid(figshape, loc=(1,1))
ax[3] = plt.subplot2grid(figshape, loc=(1,2))
i = 0
ax[i].set_title('Fitting circle in 2D coords projected onto fitting plane')
ax[i].set_xlabel('x'); ax[i].set_ylabel('y');
ax[i].set_aspect('equal', 'datalim'); ax[i].margins(.1, .1); ax[i].grid()
i = 1
ax[i].plot(P_gen[:,0], P_gen[:,1], 'y-', lw=3, label='Generating circle')
ax[i].scatter(P[:,0], P[:,1], alpha=alpha_pts, label='Cluster points P')
ax[i].set_title('View X-Y')
ax[i].set_xlabel('x'); ax[i].set_ylabel('y');
ax[i].set_aspect('equal', 'datalim'); ax[i].margins(.1, .1); ax[i].grid()
i = 2
ax[i].plot(P_gen[:,0], P_gen[:,2], 'y-', lw=3, label='Generating circle')
ax[i].scatter(P[:,0], P[:,2], alpha=alpha_pts, label='Cluster points P')
ax[i].set_title('View X-Z')
ax[i].set_xlabel('x'); ax[i].set_ylabel('z'); 
ax[i].set_aspect('equal', 'datalim'); ax[i].margins(.1, .1); ax[i].grid()
i = 3
ax[i].plot(P_gen[:,1], P_gen[:,2], 'y-', lw=3, label='Generating circle')
ax[i].scatter(P[:,1], P[:,2], alpha=alpha_pts, label='Cluster points P')
ax[i].set_title('View Y-Z')
ax[i].set_xlabel('y'); ax[i].set_ylabel('z'); 
ax[i].set_aspect('equal', 'datalim'); ax[i].margins(.1, .1); ax[i].grid()

ax[0].scatter(P_xy[:,0], P_xy[:,1], alpha=alpha_pts, label='Projected points')
ax[0].plot(xx, yy, 'k--', lw=2, label='Fitting circle')
ax[0].plot(xc, yc, 'k+', ms=10)
ax[0].legend()

t = np.linspace(0, 2*np.pi, 100)
u = P[0] - C
P_fitcircle = generate_circle_by_vectors(t, C, r, normal, u)

ax[1].plot(P_fitcircle[:,0], P_fitcircle[:,1], 'k--', lw=2, label='Fitting circle')
ax[2].plot(P_fitcircle[:,0], P_fitcircle[:,2], 'k--', lw=2, label='Fitting circle')
ax[3].plot(P_fitcircle[:,1], P_fitcircle[:,2], 'k--', lw=2, label='Fitting circle')
ax[3].legend()


ax[1].plot(C[0], C[1], 'k+', ms=10)
ax[2].plot(C[0], C[2], 'k+', ms=10)
ax[3].plot(C[1], C[2], 'k+', ms=10)
ax[3].legend()

<matplotlib.legend.Legend at 0x28fb12e7f98>

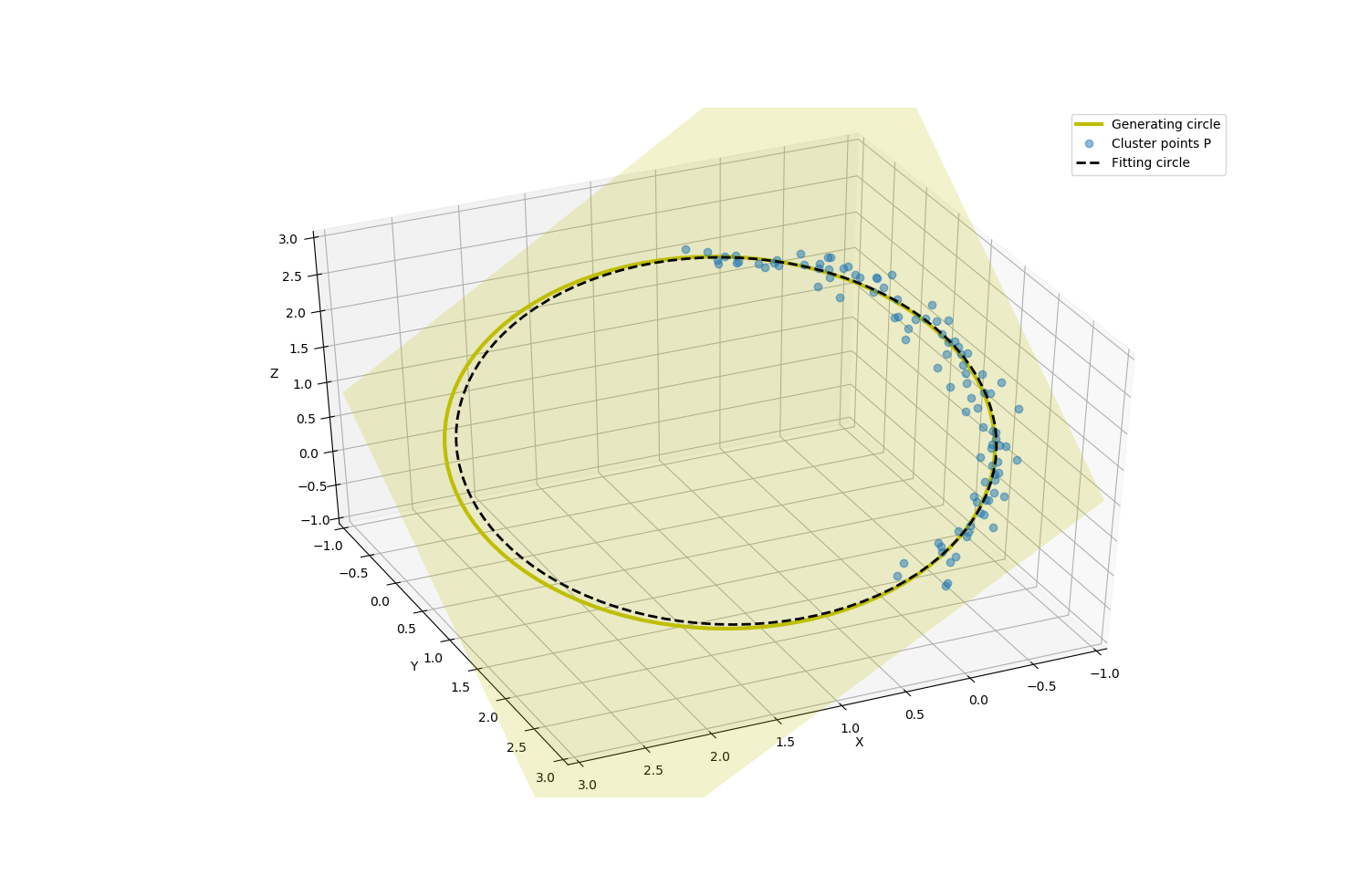
마지막으로 3차원으로 결과를 확인해보도록 하겠습니다.

%matplotlib qt

fig = plt.figure(figsize=(15,15))
ax = fig.add_subplot(1,1,1,projection='3d')
ax.plot(*P_gen.T, color='y', lw=3, label='Generating circle')
ax.plot(*P.T, ls='', marker='o', alpha=0.5, label='Cluster points P')

#--- Plot fitting plane
xx, yy = np.meshgrid(np.linspace(-1,3,11), np.linspace(-1,3,11))
zz = (-normal[0]*xx - normal[1]*yy - d) / normal[2]
ax.plot_surface(xx, yy, zz, rstride=2, cstride=2, color='y' ,alpha=0.2, shade=False)

#--- Plot fitting circle
ax.plot(*P_fitcircle.T, color='k', ls='--', lw=2, label='Fitting circle')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim(-1,3)
ax.set_ylim(-1,3)
ax.set_zlim(-1,3)
ax.legend()

# ax.set_aspect('equal', 'datalim')
# fig.set_axes_equal_3d(ax)
plt.show()

참고 문헌

[1] : FITTING A CIRCLE TO CLUSTER OF 3D POINTS
[2] : Singular Value Decomposition
[3] : Rodrigues’ rotation formula