포스트 소개
이번 포스트에서는 좌표공간에 주어진 삼각형에 외접하는 원의 중심을 구하는 방법에 대해서 알아보도록 하겠습니다. 우리는 먼저 2차원 좌표평면에서 외접원의 중심을 구해보고 이를 3차원 좌표공간으로 확장하여 외접원의 중심을 구해보도록 하겠습니다.
제가 최근에 올린 포스트의 대부분은 원의 중심과 반지름을 구하는 방법에 관한 것이었는데요. 제가 특별히 원에 집착하거나 해서 그런 것은 아니고(원을 잘 그리면 변태라는 소문이 있죠.ㅎ) 다음과 같은 이유 때문입니다.
- 먼저 원은 우리에게 친숙한 개념입니다. 또 시각화를 통해서 우리가 얻은 결과를 바로 확인할 수도 있죠.
- 다음으로, 원의 방정식은 반지름, 중심으로 매개변수화된 벡터로 나타날 수 있기 때문에 선형대수를 통해 원의 방정식을 구해볼 수 있습니다.
- 이를 통해 주어진 수학 문제를 선형대수와 연결하는 연습을 할 수 있고
- 마지막으로 우리가 유도한 선형대수 문제를 코딩을 하며 수학적 프로그래밍 사고를 기를 수 있습니다.
그럼 이제 본격적으로 주어진 삼각형에 외접하는 원의 중심을 구하는 방법을 알아볼까요?
좌표평면에 주어진 삼각형에 외접하는 원의 중심 구하기
삼각형에 외접한 원의 중심을 간단하게 외심이라고 부릅니다. 외심은 각 변의 수직이등분선이 만나는 지점에 형성됩니다. 다음 그림$^\left[1\right]$과 같이 어떤 원이 삼각형에 외접하면, 각 꼭지점과 원의 중심을 잇는 선분들은 반지름으로 같아집니다. 따라서 이 반지름들로 만들어진 삼각형들은 각각 이등변삼각형이 되고, 이등변삼각형의 성질에 의해 중심에서 대응하는 변에 내린 선분은 수직이등분선이 됩니다. 따라서 각 변의 수직이등분선이 만나는 지점이 외심이 되는거지요.

그렇다면 우리는 3개 중 2개의 수직이등분선을 직선의 방정식을 표현하고 두 직선의 교점을 구함으로써 외접원의 중심을 구할 수 있습니다. 이를 위해 2차원 좌표평면에 주어진 삼각형의 각 꼭지점을 $A(x_1, y_1),\; B(x_2, y_2),\; C(x_3, y_3)$라고 가정합시다.
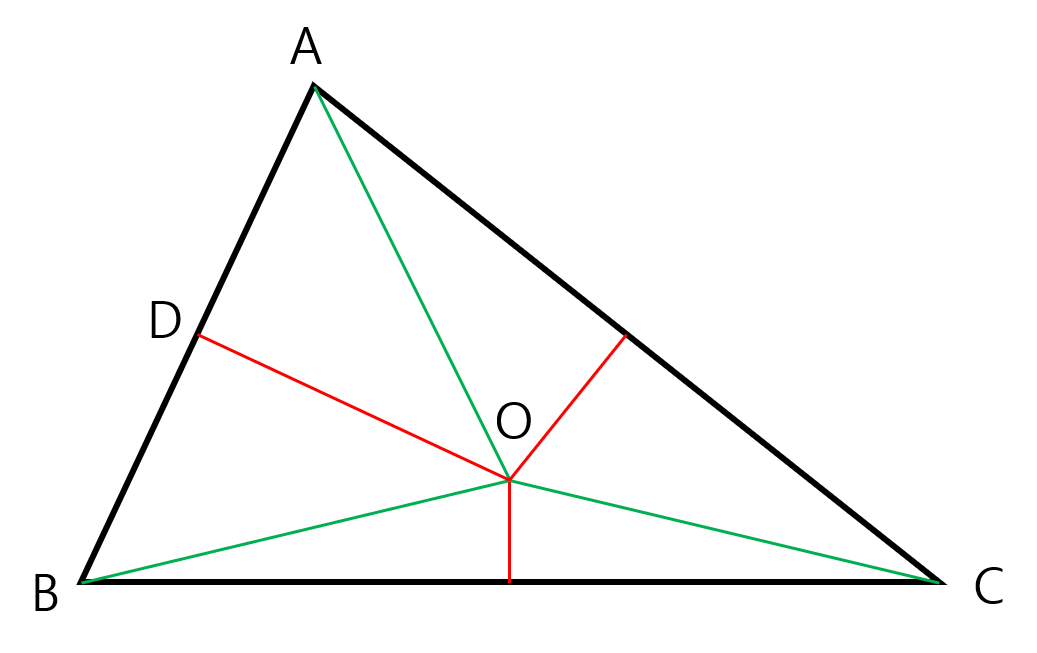
선분 $\overline{AB}$ 의 수직이등분선을 표현하는 직선의 방정식은 $\overline{DO}$ 와 $\overline{AB}$ 가 수직하다는 성질을 이용하면 쉽게 구할 수 있습니다. 외심 $O = (x, y)$라고 했을 때 $\overline{OD} = (x - \frac{x_1+x_2}{2}, y - \frac{y_1+y_2}{2})$이고 $\overline{AB} = (x_2-x_1,y_2-y_1)$ 입니다. $\overline{AB}$ 와 $\overline{DO}$ 은 서로 수직하기 때문에 두 벡터의 내적 값은 0입니다. 따라서 다음 식을 유도할 수 있습니다.
$(x_2-x_1)(x - \frac{x_1+x_2}{2}) + (y_2-y_1)(y - \frac{y_1+y_2}{2}) = 0$
선분 $\overline{BC}$에 대해서도 똑같이 식을 유도하면 다음과 같은 식이 나타납니다.
$(x_3-x_2)(x - \frac{x_2+x_3}{2}) + (y_3-y_2)(y - \frac{y_2+y_3}{2}) = 0$
두 개의 연립방정식의 해 $(x, y)$가 외심이 되는 것입니다. 연립방정식은 다음과 같이 선형대수를 이용하면 쉽게 풀 수 있습니다.
$\begin{bmatrix} x_2 - x_1 & y_2 - y_1 \\ x_3 - x_2 & y_3 - y_2 \end{bmatrix} \begin{bmatrix}x \\ y \end{bmatrix} = \frac{1}{2}\begin{bmatrix} x_2^2 - x_1^2 + y_2^2 - y_1^2 \\ x_3^2 - x_2^2 + y_3^2 - y_2^2 \end{bmatrix}$
좌표평면에서 외심을 구하는 코드는 따로 남기지 않겠습니다.
좌표공간에 주어진 삼각형에 외접하는 원의 중심 구하기
문제가 3차원 좌표공간으로 확장된다고 해서 크게 달라지는 것은 없습니다. 우리는 여전히 선분 $\overline{AB}$ 와 선분 $\overline{BC}$를 나타내는 직선의 방정식을 구할 것이고, 두 직선의 방정식이 만나는 교점을 찾아 외심으로 선택할 것입니다. 다만 두 개의 직선의 방정식을 어떻게 세우냐에 대한 전략이 조금 달라질 것입니다.
일반적으로 3차원 좌표공간에 있는 직선의 방정식은 직선이 지나는 한 점 $X_0(x_0, y_0, z_0)$ 과 방향벡터 $\mathbf{k}$ 를 알면 다음과 같이 나타낼 수 있습니다.
$\text{직선위의 점} \;\; \begin{bmatrix}x \\ y \\ z \end{bmatrix} = X_0 + \mathbf{k}\;t = \begin{bmatrix}x_0 + k_1t \\ y_0 + k_2t \\ z_0 + k_3t \end{bmatrix} \;\; \text{t는 실수}$
단순하게 $X_0$ 에서 시작해서 $\mathbf{k}$ 방향으로 $t$ 만큼 갔다고 이해할 수 있습니다. 이를 유념하면서 다시 좌표공간 위의 삼각형으로 돌아가보겠습니다.
3차원 좌표공간에 주어진 삼각형의 각 꼭지점을 $A(x_1, y_1, z_1),\; B(x_2, y_2, z_2),\; C(x_3, y_3, z_3)$라고 가정합시다. 그렇다면 선분 $\overline{AB}$의 수직이등분선은 $\overline{AB}$의 중점 $D$를 지나고 세 점을 지나는 평면의 법선벡터와 선분 $\overline{AB}$ 에 동시에 수직한 방향벡터를 갖습니다. 세 점을 지나는 평면의 법선벡터는 평면의 방정식이 $ax+by+cz = d$ 인 것을 생각하면 역시 선형대수를 이용하여 쉽게 구할 수 있습니다. $ax+by+cz = d$ 는 다시 $\frac{a}{d}x + \frac{b}{d}y + \frac{c}{d}z = 1$ 로 나타낼 수 있고 이 평면의 법선벡터는 $\mathbf{n} = (\frac{a}{d},\frac{b}{d},\frac{c}{d})$ 입니다. 사실 분모의 $d$ 는 법선벡터의 크기만 변화시킬 뿐 방향에는 영향을 미치지 않습니다. 따라서 세 점 $A, B, C$ 를 지나는 평면의 법선벡터는 다음 선형 시스템을 푸는 문제가 됩니다.
$\begin{bmatrix}x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{bmatrix} \begin{bmatrix}a \\ b \\ c \end{bmatrix} = \begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix}$
이렇게 구한 법선벡터를 $\mathbf{n}$라고 합시다. 선분 $\overline{AB}$의 수직이등분선의 방향벡터는 $\mathbf{n}$ 과 $\overline{AB}$ 와 동시에 수직합니다. 즉, 방향벡터($\mathbf{u}$)는 $\mathbf{n} \times \overline{AB}$(외적) 입니다. 수직이등분선은 $D$를 지나기 때문에 최종적으로 다음과 같이 나타낼 수 있습니다.
$\text{수직이등분선 위의 점} \;\; \begin{bmatrix}x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \frac{x_1 + x_2}{2} + u_1t \\ \frac{y_1 + y_2}{2} + u_2t \\ \frac{z_1 + z_2}{2} + u_3t \end{bmatrix}$
이 때, 실수 $t$ 값에 따라 직선 위의 점이 결정되는 것입니다. 무수히 많은 $t$ 중에 외심을 만족하는 $t^{\ast}$도 있을 것입니다. 마찬가지로 선분 $\overline{BC}$의 수직이등분선을 나타내는 직선의 방정식은 다음과 같습니다.
$\text{수직이등분선 위의 점} \;\; \begin{bmatrix}x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \frac{x_2 + x_3}{2} + v_1s \\ \frac{y_2 + y_3}{2} + v_2s \\ \frac{z_2 + z_3}{2} + v_3s \end{bmatrix}$
이 때, $\mathbf{v} = n \times \overline{BC} $ 입니다. $s$ 역시 실수에서 움직이며 직선 위의 점을 만드는 역할을 합니다. 그 중에 $s^{\ast}$ 를 외심을 만족하는 놈이라고 하면 우리의 목적은 $t^{\ast}$와 $s^{\ast}$를 찾는 것입니다. 그리고 그 때의 $\begin{bmatrix}x \\ y \\ z \end{bmatrix}$ 이 서로 같으므로 다음을 만족하는 $t$ 와 $s$ 를 푸는 문제가 됩니다.
$\begin{bmatrix} \frac{x_1 + x_2}{2} + u_1t \\ \frac{y_1 + y_2}{2} + u_2t \\ \frac{z_1 + z_2}{2} + u_3t \end{bmatrix} = \begin{bmatrix} \frac{x_2 + x_3}{2} + v_1s \\ \frac{y_2 + y_3}{2} + v_2s \\ \frac{z_2 + z_3}{2} + v_3s \end{bmatrix} $
여기서 미지수는 $t$와 $s$ 밖에 없기 때문에 다음 선형 시스템을 풀어주는 것으로 축소시킬 수 있습니다.
$\begin{bmatrix} u_1 & - v_1 \\ u_2 & - v_2 \end{bmatrix}\begin{bmatrix}t \\ s \end{bmatrix} = \begin{bmatrix} \frac{x_3 - x_1}{2} \\ \frac{y_3 - y_1}{2} \end{bmatrix}$
이 때, 왼쪽의 행렬에 singular 이슈가 있을 수 있습니다. 그 때는 당황하지 마시고 $\overline{AC}$의 방정식을 사용하면 됩니다. 이렇게 구한 $t$와 $s$ 를 두 직선의 방정식 어디에 넣든 같은 점이 나온다는 것을 확인할 수 있습니다. 그 점이 바로 원의 중심이 되는 것입니다.
파이썬 코드로 확인하기
지금까지 아주 길게 외접원의 중심을 구하는 방법을 알아보았습니다. 마지막으로 파이썬 코드를 통해 위 결과를 확인해보도록 하겠습니다. 코드가 어렵지 않고 충분한 주석을 달았기 때문에 자세한 설명은 생략하도록 하겠습니다.
import numpy as np
def get_center(a, b, c):
# ----------------------------------------
# Find the normal vector from three points a, b, c
# ----------------------------------------
X = np.array([a, b, c])
y = [1, 1, 1]
n = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
n = n/np.linalg.norm(n)
# ----------------------------------------
# Find u (v) perpendicular to vector ab (bc) and to the normal vector at the same time
# This can be obtained by cross-product between ab and n (bc and n)
# ----------------------------------------
u = np.cross(b-a, n)
v = np.cross(c-b, n)
# ----------------------------------------
# Find the parameter t (s) of the linear eqauation of the vertical bisector line of ab (bc) satisfying the center
# ----------------------------------------
X = np.array([[u[0], -v[0]], [u[1], -v[1]]])
y = np.array([(c[0] - a[0])/2, (c[1] - a[1])/2])
t = np.linalg.inv(X).dot(y)
# ----------------------------------------
# return the center of the circle
# ----------------------------------------
return (a+b)/2 + u*t[0]
원 만드는 함수, [2]를 참고하였습니다.
def generate_circle_by_angles(t, C, r, theta, phi):
# Orthonormal vectors n, u, <n,u>=0
n = np.array([np.cos(phi)*np.sin(theta), np.sin(phi)*np.sin(theta), np.cos(theta)])
u = np.array([-np.sin(phi), np.cos(phi), 0])
# P(t) = r*cos(t)*u + r*sin(t)*(n x u) + C
P_circle = r*np.cos(t)[:,np.newaxis]*u + r*np.sin(t)[:,np.newaxis]*np.cross(n,u) + C
return P_circle
np.random.seed(1) # 커널을 다시 시작해도 같은 샘플링을 할 수 있게함
r = 2.5 # 반지름
C = np.array([3,3,4]) # 중심
theta = 45/180*np.pi # Azimuth
phi = -30/180*np.pi # Zenith
# 원의 방정식에서 등간격으로 점 24개를 뽑기
t = np.linspace(0, 2*np.pi, 24, endpoint=False)
P_gen = generate_circle_by_angles(t, C, r, theta, phi)
# 만든 점 중에 3개 뽑기, 중복(replace) 불허
points = np.random.choice(range(24) , 3, replace = False)
X = P_gen[points]
get_center(X[0], X[1], X[2])
array([3., 3., 4.])
참고문헌
[1] : 외접원 이미지
[2] : FITTING A CIRCLE TO CLUSTER OF 3D POINTS

