2차원 좌표평면에 $n$개의 점이 주어졌다고 가정하자 : ${(x_1, y_1), (x_2, y_2), \cdots ,(x_n, y_n) }$
이 때 이 데이터에 가장 잘 맞는 원을 어떻게 구할 수 있을까? 최소제곱법(method of least squares) 관점에서 문제를 해결해보자.
데이터를 생각하기 전에 먼저 원의 방정식을 생각해보자. 다들 잘 알고 있는 것처럼 중심이 $(x_c, y_c)$이고 반지름이 $r$ 인 원의 방정식은 다음과 같다.
$(x-x_c)^2 + (y - y_c)^2 = r^2$
이를 조금만 더 정리해서 선형대수스럽게 만들어보자.
$(x-x_c)^2 + (y - y_c)^2 = r^2$
$x^2 + y^2 -2(xx_c + yy_c) + x_c^2 + y_c^2 = r^2$
$2(xx_c + yy_c) + (r^2 - x_c^2 - y_c^2) = x^2 + y^2$
$2x_cx + 2y_cy + (r^2 - x_c^2 - y_c^2) = x^2 + y^2$
이 때, $\mathbf{c} = (c_0, c_1, c_2)$라고 하면 다음과 같이 쉽게 정리할 수 있다.
$c_0 + c_1x + c_2y = x^2 + y^2$
where $c_0 = r^2 - x_c^2 - y_c^2$, $c_1 = 2x_c$, $c_2 = 2y_c$
여기서 $x$와 $y$가 데이터로 주어졌다면, 즉, $x$, $y$, $x^2 + y^2$ 이 어떤 숫자로 정해져있다면 위 방정식을 미지수가 $c_0$, $c_1$, $c_2$인 연립방정식으로 볼 수 있다. 즉, 데이터로부터 원의 방정식을 찾는다는 것은 위 연립방정식들을 풀어서 $\mathbf{c}$를 찾는 것이다.
이를 유념하면서 $n$개의 데이터 ${(x_1, y_1), (x_2, y_2), \cdots ,(x_n, y_n) }$ 가 원 위에 있다고 생각해보자. 이는 $n$개의 연립방정식이 있다는 것이며 이를 다음과 같이 선형계로 표현할 수 있을 것이다.
$A\mathbf{c} = \mathbf{b}$
이 때 $A = \begin{bmatrix} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & y_n \\ \end{bmatrix}, \mathbf{b} = \begin{bmatrix} x_1^2 + y_1^2 \\ x_2^2 + y_2^2 \\ \vdots \\ x_n^2 + y_n^2 \\ \end{bmatrix} $ 이다.
물론 실제로는 모든 데이터가 한 원 위에 있지 않을 것이기 때문에 등호는 성립하지 않을 것이고 우리는 가능한 모든 $\mathbf{c}$ 중에 오차를 가장 작게 만들어주는 $\hat{\mathbf{c}}$를 찾는 것이다. 즉,
$\hat{\mathbf{c}} = \operatorname{argmin}_\mathbf{c}\lVert \mathbf{b}-A\mathbf{c} \rVert^2$
를 풀어야 하는 것이다. 선형회귀를 공부하신 분들은 위 식의 해 $\hat{\mathbf{c}}$가 다음과 같이 결정된다는 것을 알고 있을 것이다.
$\hat{\mathbf{c}} = (A^TA)^{-1}A^T\mathbf{b}$
이렇게 구한 $\hat{\mathbf{c}}$와 위에서 언급한 $x_c, y_c$의 관계를 통해 원의 방정식을 구하면 된다.
지금까지 이야기한 것들을 파이썬을 통해 눈으로 직접 한 번 확인해보자.
먼저 원을 한 번 그려보자. 원 위의 모든 점은 반지름 $r$과 점과 $x$축이 이루는 각 $\theta$로 나타낼 수 있다. 예를 들어 중심이 원점이고 반지름 길이가 $r$인 원 위의 모든 점 $(x, y)$는 $(rcos\theta , rsin\theta )$처럼 나타낼 수 있다. ($0\le \theta \le 2\pi$) 이 점을 유념하면 원 그리는 것을 어렵지 않다.
import numpy as np
import matplotlib.pyplot as plt
def make_circle(c, r):
theta = np.linspace(0, 2 * np.pi, 256)
x = r * np.cos(theta)
y = r * np.sin(theta)
return np.vstack((x, y)).T + c
c = np.array([2, 3])
r = 1.5
circle = make_circle(c, r)
plt.figure(figsize = (4,4))
plt.plot(circle[:,0], circle[:, 1], 'b-')
plt.grid()
plt.xlim(0,5)
plt.ylim(0,5)
plt.show()
자 이제 원의 방정식에서 추출됐을 것으로 가정되는 데이터를 만들어보자. 우리는 circle 변수에 임의로 점을 추출해 노이즈를 추가하는 방식으로 데이터셋을 만들 것이다.
# circle 변수에서 20개 추출
idx = np.random.choice(len(circle), 15)
A = circle[idx]
# 가우시안 노이즈 추가
A = A + 0.09 * np.random.randn(A.shape[0], A.shape[1])
plt.figure(figsize = (4,4))
plt.plot(circle[:,0], circle[:, 1], 'b-')
plt.scatter(x = A[:,0], y = A[:, 1], color = 'r')
plt.grid()
plt.xlim(0,5)
plt.ylim(0,5)
plt.show()
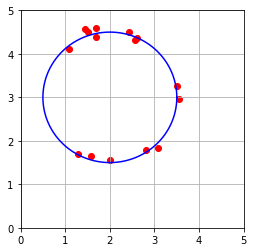
$A = \begin{bmatrix} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & y_n \\ \end{bmatrix}, \mathbf{b} = \begin{bmatrix} x_1^2 + y_1^2 \\ x_2^2 + y_2^2 \\ \vdots \\ x_n^2 + y_n^2 \\ \end{bmatrix} $ 를 만들어보자
ones = np.ones((A.shape[0], 1))
A = np.concatenate((ones, A), axis = 1)
b = A[:,1] ** 2 + A[:,2] ** 2
# 상위 5개만 출력
A[:5, :]
array([[1. , 3.54583387, 2.96857292],
[1. , 1.70072577, 4.58310647],
[1. , 1.68745782, 4.39352026],
[1. , 1.50438585, 4.50694513],
[1. , 1.43481828, 4.57897573]])
# 상위 5개만 출력
b[:5]
array([21.38536301, 23.89733305, 22.15053421, 22.57573124, 23.02572228])
$\hat{\mathbf{c}} = (A^TA)^{-1}A^T\mathbf{b}$ 을 통해 $\hat{\mathbf{c}}$ 을 구할 수 있다.
c = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(b)
# or you can do this just by using
# np.linalg.lstsq(A, b, rcond=None)[0]
자 거의 다 왔다. 마지막으로 $c_0 = r^2 - x_c^2 - y_c^2$, $c_1 = 2x_c$, $c_2 = 2y_c$ 을 통해 원의 중심 $(x_c, y_c)$와 반지름 $r$을 구해주면 된다.
def return_circle(c):
x_c = c[1] / 2
y_c = c[2] / 2
r = c[0] + x_c ** 2 + y_c ** 2
return x_c, y_c, np.sqrt(r)
x_c, y_c, r_c = return_circle(c)
print(x_c, y_c, r_c)
2.024428982244557 3.036383629584562 1.5055415787422162
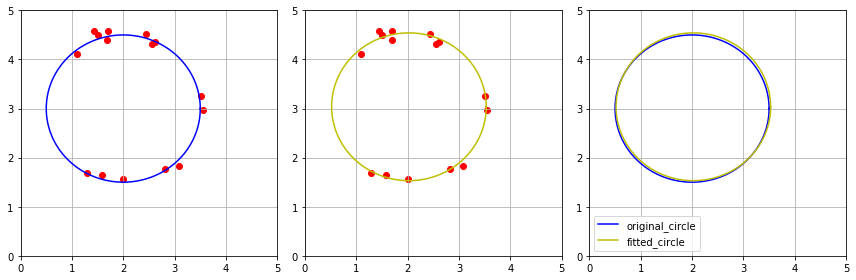
우리는 중심이 (2,3)이고 반지름이 1.5인 원에서 데이터를 추출했었고, 추출한 데이터에 노이즈를 추가해준 후 2차원 circle fitting을 실시하였다. 추출한 데이터로부터 구한 원은 중심이 (2.02, 3.03)이고 반지름이 1.505 였다. 마지막으로 결과를 시각화하며 이번 포스트를 마치도록 하겠다. 다음 포스트에서는 좌표평면이 아닌 좌표공간에 있는 데이터로부터 원을 적합시키는 방법에 대해 알아보도록 하겠다.
fitted_circle = make_circle(np.array([x_c, y_c]), r_c)
plt.figure(figsize = (12,4))
plt.subplot(131)
plt.plot(circle[:,0], circle[:, 1], 'b-', label = 'original_circle')
plt.scatter(x = A[:,1], y = A[:, 2], color = 'r', label = 'sampled point')
plt.grid()
plt.xlim(0,5)
plt.ylim(0,5)
plt.subplot(132)
plt.plot(fitted_circle[:,0], fitted_circle[:, 1], 'y-', label = 'fitted_circle')
plt.scatter(x = A[:,1], y = A[:, 2], color = 'r', label = 'sampled point')
plt.grid()
plt.xlim(0,5)
plt.ylim(0,5)
plt.subplot(133)
plt.plot(circle[:,0], circle[:, 1], 'b-', label = 'original_circle')
plt.plot(fitted_circle[:,0], fitted_circle[:, 1], 'y-', label = 'fitted_circle')
plt.grid()
plt.legend()
plt.xlim(0,5)
plt.ylim(0,5)
plt.tight_layout()
plt.show()
reference
FITTING A CIRCLE TO CLUSTER OF 3D POINTS

