유한차분을 이용한 미분값 근사
유한차분법 (Finite Difference Method, FDM)은 미분방정식을 수치적으로 풀이하는 방법이며, 도함수를 유한차분을 이용하여 근사하는 것이 핵심이다. 이번 포스팅 시리즈에서는 유한차분법을 이용하여 미분방정식을 수치적으로 풀이하는 방법에 대해 다뤄볼 예정이다. 먼저 smooth 함수 $u:\mathbb{R} \rightarrow \mathbb{R}$가 주어졌다고 하자. smooth 함수라고 하면 보통 원하는 횟수만큼 미분 가능한 함수를 말한다. 미분에 대해 이야기할 것이니 앞으로 미분가능한 함수만 고려하겠다는 의미다.
우리의 목표는 $u(x)$의 도함수 $u’(x)$를 계산하는 것이다. 물론, 중고등학교 때 배운 미분공식들을 사용하여 해석적으로 도함수를 계산할 수 있다. 하지만 여러 이유로 도함수를 해석적으로 계산하지 못할 때가 있다. 한 가지 상황을 예를 들자면, $u(x)$의 식이 주어지지 않고 특정 몇 개의 점에서 함수값만 알고 있을 수도 있다. 이때는 도함수를 해석적으로 계산하지 못하고 수치적으로 근사해야만 한다.
$x$에서의 도함수 $u’(x)$는 $x$와 $x$ 주변의 점을 이용해서 근사할 수 있다. 충분히 작은 양수 $h>0$에 대해서 $x$와 $x+h$에서의 함수값을 알 때, forward difference는 다음과 같이 미분값에 근사한다. \[D_{+}u(x):=\frac{u(x+h) - u(x)}{(x+h) - x}=\frac{u(x+h) - u(x)}{h}. \quad \quad (1)\]
두 점 $x$와 $x-h$를 사용해서 미분값을 근사시킬 수도 있다. backward difference는 다음과 같이 미분값에 근사한다. \[D_{-}u(x):=\frac{u(x) - u(x-h)}{x - (x-h)}=\frac{u(x) - u(x-h)}{h}. \quad \quad (2)\]
$u’(x)$를 구하는 것이 목표지만 굳이 $u(x)$를 쓰지 않고 $u(x-h)$와 $u(x+h)$를 사용해도 좋다. central difference는 다음과 같이 미분값에 근사한다. \[D_{0}u(x):=\frac{u(x+h) - u(x-h)}{(x+h) - (x-h)}=\frac{u(x+h) - u(x-h)}{2h}. \quad \quad (3)\]
혹자는 함수값 2개만 사용하는 것이 아니라, 함수값 4개를 사용해서 미분값을 근사시킬 수도 있다. 예를 들어, 네 점 $x+h, x, x-h, x-2h$을 사용하여 미분값을 근사시킬 수 있다. \[D_{3}u(x):=\frac{1}{6h}\left[2u(x+h)+3u(x)-6u(x-h)+u(x-2h)\right]. \quad \quad (4)\]
계수들이 어떻게 결정되는지는 잠시 후에 알아보자.
수치적 방법론들의 수렴률 / 정확도
위의 예시들에서 알 수 있는 것처럼, 미분값 $u(x)$에 근사하기 위해 다양한 조합의 함수값들을 사용할 수 있다. 일반적으로 많은 점들을 사용할 수록 실제 미분값과 근사값 사이의 오차가 빠르게 감소한다. 오차가 작은거면 작은거지 오차가 빠르게 감소한다는 표현은 무엇일까? 위의 예시들에서 $h$를 충분히 작은 양수라고만 소개하였다. 이 $h$ 값에 따라서 오차가 달라진다. 일반적으로 $h$가 작으면 작을수록 오차도 작아진다. 다시 돌아와서 “오차가 빠르게 감소한다”라는 것은 오차의 수렴률에 대한 이야기이다. 보통 빅오 표기(big O notation)를 사용해서 수치적 방법론들의 수렴률 (또는 정확성)을 나타낸다.
어떤 함수 $f(h), g(h)$에 대해서 $f(h)=\mathcal{O}(g(h))$ as $h \rightarrow 0$라는 것은 $f$가 $g$만큼 빠르게 감소한다는 것을 의미한다. 정확한 정의는 충분히 작은 모든 $h$에 대하여 \(\left| \frac{f(h)}{g(h)} \right| < C,\)
인 상수 $C$를 찾을 수 있을 경우 $f(h)=\mathcal{O}(g(h))$ as $h \rightarrow 0$라고 한다. 예를 들어, $f(h)=\mathcal{O}(h^2)$의 의미는 $h$가 0으로 갈 때, $f$는 최소한 $h^2$이 0으로 가는 속도만큼 빠르게 0으로 간다는 것을 의미한다. 다시 돌아와서 식 $(1)$과 $(2)$는 $\mathcal{O}(h)$이고, 식 $(3)$은 $\mathcal{O}(h^2)$ 이며, 식 $(4)$는 $\mathcal{O}(h^3)$이다. 수렴률을 구하는 방법은 잠시 후에 알아보자.
그렇다고 무조건 많은 함수값을 사용하는 것이 좋은 것은 아니다. 오차는 줄어들 수 있겠지만 그만큼 많은 함수값 계산이 필요하기 때문에 수치적 풀이에 많은 시간이 소요될 수도 있다. 계산 속도와 오차 사이의 트레이드 오프 관계에서 적당히 좋은 방법론을 사용해야 할 것이다.
[실습]
$u(x)=\sin(x)$라고 할 때, $x=1$에서의 $u’(x)$ 값을 수치적으로 구해보자. 실제 미분값은 $\cos(1)$일 것이다. $h$ 값이 각각 $0.1, 0.05, 0.01, 0.005, 0.001$일 때 근사값을 구할 것이다. 마지막으로 실제 미분값에서 근사값을 빼줘서 오차의 크기를 출력해볼 것이다.
import numpy as np
def u(x):
return np.sin(x)
h_list = [1e-1, 5e-2, 1e-2, 5e-3, 1e-3]
x = 1
results = []
for h in h_list:
D_plus = (u(x + h) - u(x)) / h
D_minus = (u(x) - u(x - h)) / h
D_0 = (u(x + h) - u(x - h)) / 2 / h
D_3 = (2 * u(x + h) + 3 * u(x) - 6 * u(x - h) + u(x - 2 * h)) / 6 / h
results.append([D_plus, D_minus, D_0, D_3])
results = np.cos(1) - np.array(results)
print(results)
[[ 4.29385533e-02 -4.11384459e-02 9.00053698e-04 -6.82069338e-05]
[ 2.12574901e-02 -2.08072945e-02 2.25097822e-04 -8.64914174e-06]
[ 4.21632486e-03 -4.19831487e-03 9.00499341e-06 -6.99412992e-08]
[ 2.10592434e-03 -2.10142182e-03 2.25125680e-06 -8.75402917e-09]
[ 4.20825508e-04 -4.20645407e-04 9.00504502e-08 -6.99794667e-11]]
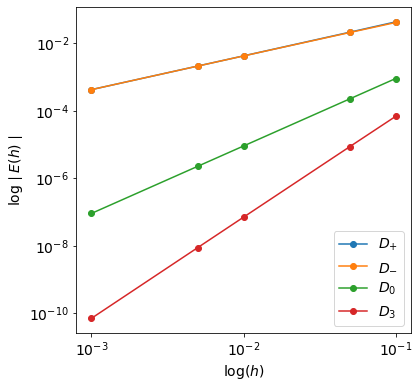
출력물의 열들은 각각 $D_{+}, D_{-}, D_{0}, D_{3}$을 나타내고, 행들은 $h$ 값을 나타낸다. 수치적으로 보는 것은 가시성이 좋지 않으니 오차를 시각화해보자. 오차 시각화는 보통 $\log (h)$에 따른 $log \left| E(h) \right|$를 시각화 한다. 그 이유는 위에서 본 수렴률과 상관 있다. 보통 오차의 수렴률을 $E(h)=\mathcal{O}(h^p)$와 같이 나타내는데, 빅오의 정의에 따라 $E(h) \approx Ch^p$이고 양변에 로그를 취해주면 다음과 같이 직선의 방정식 형태로 나타낼 수 있기 때문이다. 기울기가 order $p$이다. \[\log \left| E(h) \right| \approx \log \left| C \right| + p \log h\]
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14
results = np.abs(results)
plt.figure(figsize=(6, 6))
plt.plot(np.log10(h_list), np.log10(results[:, 0]), 'o-', label='$D_{+}$')
plt.plot(np.log10(h_list), np.log10(results[:, 1]), 'o-', label='$D_{-}$')
plt.plot(np.log10(h_list), np.log10(results[:, 2]), 'o-', label='$D_{0}$')
plt.plot(np.log10(h_list), np.log10(results[:, 3]), 'o-', label='$D_{3}$')
plt.xticks(ticks=[-3, -2, -1], labels=['$10^{-3}$', '$10^{-2}$', '$10^{-1}$'])
plt.yticks(ticks=[-2, -4, -6, -8, -10], labels=['$10^{-2}$', '$10^{-4}$', '$10^{-6}$', '$10^{-8}$', '$10^{-10}$'])
plt.xlabel("$\log (h)$")
plt.ylabel("$\log \mid E(h) \mid$")
plt.legend()
plt.show()