Chapter 1. Introduction

Graph Representation Learning Book 읽고 정리하기 시리즈 중 첫 번째 이야기. 부디 완주하게 기도해주세요 !

1.1 What is graph?

• 그래프는 복잡한 시스템을 설명하기 위한 일반적인 자료구조 중 하나이다.
• 그래프는 다수의 객체 (노드)들과 객체 사이의 관계 (엣지)들의 집합이다.
• 그래프는 “객체 그 자체”보다 “객체 사이의 관계”에 초점을 맞춘다.

그래프의 정의

• 그래프 $G=(V,E)$는 노드들의 집합 $V$와 엣지들의 집합 $E$으로 정의된다. 노드 $u \in V$에서 노드 $v \in V$로 가는 엣지를 $(u, v) \in E$라고 표기한다.
• Simple 그래프: 한 노드쌍에 최대 1개의 엣지만을 가지며, 노드 자기 자신을 연결하는 엣지 (루프)가 없는 undirected 그래프를 simple 그래프라고 부른다. 이 책에서 다루는 대부분의 그래프는 simple 그래프이다.

인접행렬

• 그래프 $G$의 각 노드에 순서 (인덱스)를 부여했을 때, 인접행렬 $\mathbf{A} \in \mathbb{R}^{\mid V \mid \times \mid V \mid}$은 다음과 같이 정의된다.
  • $\mathbf{A}[u, v] = \begin{cases}1 & \quad \text{if } (u, v) \in E \\ 0 & \quad \text{otherwise}\end{cases}$
    
• Weighted 그래프의 경우 각 노드쌍마다 연결 강도 $w_{i, j}$가 있으며, 이때의 인접행렬 $\mathbf{A}$의 $u$행 $v$열의 원소는 다음과 같다.
  • $\mathbf{A}[u, v] = w_{u,v}$

그래프 vs 네트워크?

• 그래프란 용어는 머신러닝에서 많이 사용된다.
• 네트워크란 용어는 데이터마이닝에서 많이 사용된다.
• 또는 추상적인 자료구조를 이론적으로 설명할 땐 그래프, 그리고 그래프로 표현되는 실제 데이터들은 네트워크라고 부를 수도 있다

1.1.1 Multi-relational 그래프

• 두 종류 이상의 관계에 대한 연결성을 나타낼 수 있는 그래프 $G=(V, E, R)$
  • 예를 들어, 노드가 사람을 나타내고 엣지는 “친구 관계”를 나타내는 소셜 네트워크가 있다고 하자. 하지만, 두 사람 사이의 “차단 관계”도 네트워크에 표현하고 싶을 수 있을 것이다. 이때, 원래 네트워크의 엣지 집합 $E$에 “차단 관계” 엣지를 추가하면 $E$안의 어떤 엣지가 “친구 관계” 인지 “차단 관계”인지 알 수 없을 것이다. 따라서, 관계의 종류도 추가하여 엣지를 표현한 그래프를 multi-relational 그래프라고 한다.
• 두 노드 $u, v \in V$가 관계 $\tau \in R$ 에 대해 연결되어 있다면 $(u, \tau, v) \in E$ 이다. 각 종류의 관계 $\tau$마다 인접행렬 $\mathbf{A}_\tau$가 있으며, 전체 그래프는 인접행렬을 쌓아올린 형태의 3차원 인접텐서 $\mathbf{A} \in \mathbb{R}^{\mid V \mid \times \mid R \mid \times \mid V \mid}$로 나타낼 수 있다.

Heterogeneous 그래프

• 노드 집합 $V$가 disjoint subsets의 합집합으로 분리될 수 그래프이다. 즉, $V=V_1 \cup V_2 \cup \cdots \cup V_k$ where $V_i \cap V_j = \emptyset$ for all $i \ne j$.
  • 예를 들어, 유저가 구매한 상품을 나타내는 네트워크에서는 유저 노드와 상품 노드가 있을 것이다. 그러면, 전체 노드 집합 $V$는 유저 노드 집합 $V_{\text{유저}}$와 상품 노드 집합 $V_{\text{상품}}$으로 나눌 수 있을 것이다. 유저이면서 상품인 대상은 없을 것이다.
• 한 종류의 관계 $\tau_i$ 는 특정 두 노드 부분 집합 사이의 연결을 나타낸다. 즉, $(u, \tau_i, v) \in E \rightarrow u \in V_j, v \in V_k$
  • 예를 들어, 위의 예시에서 유저와 유저를 연결하는 관계 $\tau_{\text{유저,유저}}$와 상품과 상품을 연결하는 관계 $\tau_{\text{상품, 상품}}$, 그리고 유저와 상품을 연결하는 관계 $\tau_{\text{유저, 상품}}$가 있을 수 있다.
• 이때, $j \ne k$인 경우를 multipartite 그래프라고 부른다.
  • 예를 들어, 위의 예시에서 $\tau_{\text{유저, 상품}}$에 대한 엣지만 있는 네트워크를 multipartite 그래프라고 한다.

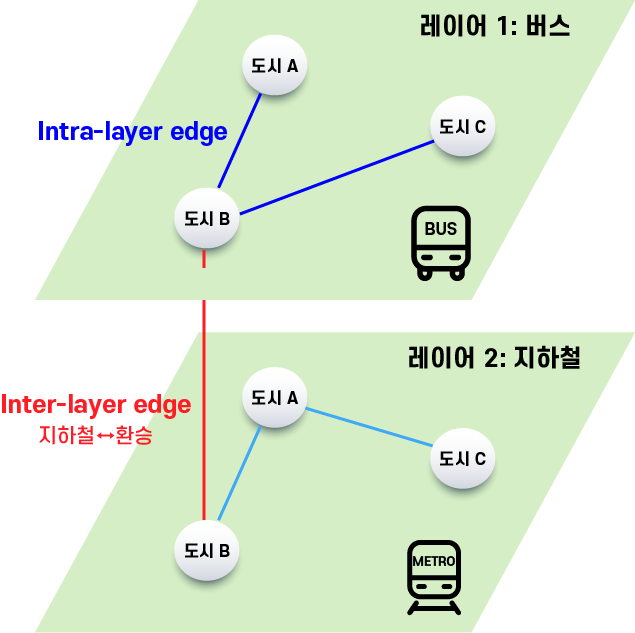
Multiplex 그래프

• 각 종류의 관계에 대응하는 $k$개의 layer가 있다.
• 모든 노드는 모든 layer에 모두 속해 있다.
• intra-layer 엣지는 layer 안에서 연결되는 엣지이다.
• inter-layer 엣지는 서로 다른 두 layer에서 같은 노드끼리 연결되는 엣지이다.
• 예) 노드: 도시 / layer: 교통수단 / intra-layer edge: 해당 교통수단으로 두 도시를 이동할 수 있으면 연결 / inter-layer edge: 어떤 한 도시에서 두 교통수단을 환승할 수 있으면 연결

1.1.2 Feature information

• 노드에 부여된 속성값으로서, attribute 또는 feature라고 한다.
  • 소셜 네트워크의 경우, 한 사람 노드에 대해서 나이, 성별, 지역 등을 feature로 가질 수 있다.
• 각 노드 $u \in V$ 에 대해서 $m$개의 feature를 갖고 있는 경우, 우리가 흔히 보는 테이블 데이터 형태로 저장할 수 있다.
  • 즉, $\mathbf{X} \in \mathbb{R}^{\mid V \mid \times m}$으로 노드별 feature 정보를 표현할 수 있다.
  • Heterogeneous 그래프의 경우 노드 부분 집합마다 다른 feature set을 갖는 경우도 있다.
• 간혹 엣지 또는 그래프마다 feature가 있는 경우도 있다.

1.2 Machine learning on graphs

• 이번 섹션에서는 그래프 데이터와 관련된 테스크들에 대해서 알아본다.
• (참고) 그래프 데이터에 대해서는 지도 학습과 비지도 학습을 구분하는 것이 모호하다.

1.2.1 Node classification

• 주어진 소량의 레이블링된 노드로부터 학습하여, 레이블되어 있지 않은 노드들의 클래스를 분류하는 문제
• 가장 인기 있는 문제 중 하나이다.

기존 지도 학습 모델과 다른점

• i.i.d를 가정하는 일반적인 지도 학습 모델과는 다르게 그래프 안의 노드들은 i.i.d가 아니기 때문에 상호연결을 모델링할 수 있어야 한다.

접근 방법

• homophily (동종 선호): 이웃된 노드들끼리는 비슷한 feature를 가질 것이라고 가정하는 방법
• heterophily (이종 선호): 자신과 다른 label을 갖는 노드와 우선적으로 연결될 것이라고 가정하는 방법
• structural equivalence: 이웃 연결 구조가 비슷한 노드끼리는 같은 label을 가질 것이라고 가정하는 방법

준지도학습?

• 그래프 안에서 레이블링되지 않은 노드와의 연결성도 학습에 사용

1.2.2 Relation prediction

• 그래프 안의 노드와 노드 사이의 연결성을 예측하는 문제
• 문제를 적용하는 도메인에 따라서 다양한 이름으로 불린다.
  • link prediction, graph completion, relational inference 등

문제 정의

• 주어진 노드 집합 $V$와 부분적으로만 알고 있는 엣지 부분 집합 $E_{train} \subset E$을 사용하여 $e \in E \setminus E_{train}$의 연결성을 예측하는 것

Inductive bias

• 귀납적 추론 (훈련 데이터$\rightarrow$일반적인 도메인) 을 수행하기 위한 학습 모델이 갖고 있는 가정들의 집합
  • 예를 들어, 선형회귀는 데이터 사이의 선형관계를 가정
• 그래프 데이터에서는 순서가 없기 때문에 permutation invariance를 가정하는 모델이 필요

1.2.3 Clustering and community detection

• 주어진 그래프에서 노드들의 커뮤니티 (군집)를 포착하는 문제
• 같은 커뮤니티에 있는 노드들끼리 더 연결성이 있을 것이다.
• 주어진 그래프의 latent 커뮤니티 구조를 추론하는 것이 어려운 문제이다.

1.2.3 Clustering and community detection

• 주어진 그래프에서 노드들의 커뮤니티 (군집)를 포착하는 것
• 같은 커뮤니티에 있는 노드들끼리 더 연결성이 있을 것이다.
• 주어진 그래프의 latent 커뮤니티 구조를 추론하는 것이 어려운 문제이다.

1.2.4 그래프 분류, 회귀, 군집

• 주어진 여러 그래프들에 대해서 각 그래프의 클래스나 타겟값을 예측하는 문제
• 각각의 그래프는 i.i.d라고 가정할 수 있다.
• 그래프 안의 노드 사이 관계성을 고려하면서 그래프의 feature를 뽑을 수 있어야 한다.

참고문헌

[1] Hamilton, William L.,Graph Representation Learning, Synthesis Lectures on Artificial Intelligence and Machine Learning, 14, pp.1-159