16. Proximal Policy Optimization (PPO)

지난 장에서 다루었던 TRPO의 핵심은 정책의 monotonic improvement가 보장되는 영역 내에서 정책 네트워크의 파라미터를 업데이트한다는 점이다. 말은 어렵지만, 현재 정책과 “가까운 정책들 중에서” performance measure를 증가시키는 정책을 찾는 것으로 구현된다. TRPO는 목적함수를 최대화하는 방향 (그레디언트 방향)으로 현재 정책과의 KL divergence가 \(\delta\)보다 작아질 때까지 backtrack line search를 하며 조건을 만족시키는 파라미터를 찾았다. PPO는 특정 조건을 만족시키는 파라미터를 찾기 보다는 그냥 애초에 TRPO의 업데이트 크기를 clip하여 정책을 조금씩만 업데이트 하는 방법이라고 요약할 수 있다.

---

16.1. TRPO의 목적함수 복습

TRPO는 업데이트 전 정책 \(\pi_{\theta_{\text{old}}}\)와 업데이트 후 정책 \(\pi_{\theta}\)의 KL divergence에 대한 제약 (constraint)을 걸어 다음 surrogate objective를 최대화를 했다 (참고로 실제 최적화하고 싶은 목적함수의 lower bound를 최적화하기 때문에 surrogate objective라고 부른다).

\[ \operatorname*{maximize}_\theta \hat{\mathbb{E}}_t \left[ \frac{\pi_{\theta}\left( a_t |s_t\right)}{\pi_{\theta_{\text{old}}}\left( a_t |s_t\right)} \hat{A}_t\right], \quad \quad (1) \]

\[ \text{subject to} \quad \hat{\mathbb{E}}_t \left[ \operatorname{KL}\left[ \pi_{\theta_{\text{old}}}\left( \, \cdot \,|s_t \right), \pi_\theta \left( \, \cdot \, | s_t \right) \right] \right] \le \delta. \quad \quad (2) \]

해석하자면,

• 정책은 주어진 상태에 대한 행동들의 확률분포이기 때문에 두 정책 사이의 KL divergence를 계산할 수 있다.

• 업데이트 전, 후 정책의 KL divergence를 \(\delta\) 이하로 유지하면서 식 \((1)\)의 surrogate objective를 최대화.

• TRPO에서는 식 \((1), (2)\)의 constraint optimization 대신 아래의 \((3)\)을 최대화하는 방법도 제안했지만, \(\beta\) 값을 하나로 정하는 것이 매우 어렵다고 한다. \(\beta\)를 환경에 따라 지정해줘야할 뿐만 아니라, 사실 학습 도중에도 adaptive하게 바꿔줘야할 필요가 있었다.

\[ \operatorname*{maximize}_{\theta} \hat{\mathbb{E}}_t \left[ \frac{\pi_{\theta}\left( a_t |s_t\right)}{\pi_{\theta_{\text{old}}}\left( a_t |s_t\right)} \hat{A}_t -\beta \operatorname{KL}\left[ \pi_{\theta_{\text{old}}}\left( \, \cdot \,|s_t \right), \pi_\theta \left( \, \cdot \, | s_t \right)\right] \right]. \quad \quad (3) \]

---

16.2. PPO 알고리즘 구성요소들

16.2.1. Clipped surrogate objective

PPO는 KL divergence를 이용하여 업데이트의 크기를 제한하지 않고, 애초에 업데이트 대상인 \(\frac{\pi_{\theta}\left( a_t |s_t\right)}{\pi_{\theta_{\text{old}}}\left( a_t |s_t\right)} \hat{A}_t\)의 값을 clipping하여 제한하는 clipped surrogate objective를 사용한다. 표기의 편의를 위해 \(r_{t} \left( \theta \right) = \frac{\pi_{\theta} \left( a_t | s_t \right)}{\pi_{\theta_{\text{old}}} \left( a_t | s_t \right)}\)라고 하자.

\[ L^{\text{CLIP}}(\theta)=\hat{\mathbb{E}}_t \left[ \min \left(r_t \left(\theta\right)\hat{A}_t, \operatorname{clip}\left(r_t \left(\theta\right), 1-\epsilon,1+\epsilon \right) \hat{A}_t \right) \right], \quad \quad (4) \]

where

\[\begin{split} \operatorname{clip}\left(x, \text{low}, \text{high} \right)=\begin{cases} \text{low} & \text{if } x<\text{low}, \\ x & \text{if } \text{low} \le x < \text{high}, \\ \text{high} & \text{if } x \ge \text{high}. \end{cases} \end{split}\]

우선 \(\theta = \theta_{\text{old}}\)일 때 \(r_t \left( \theta \right)=1\)에서 업데이트를 시작한다. 참고로 환경과 상호작용하여 데이터를 수집한 정책 네트워크의 현재 파라미터가 \(\theta_{\text{old}}\)이다. 수집한 데이터로 정책을 \(K\) epochs 훈련시킬 것이다.

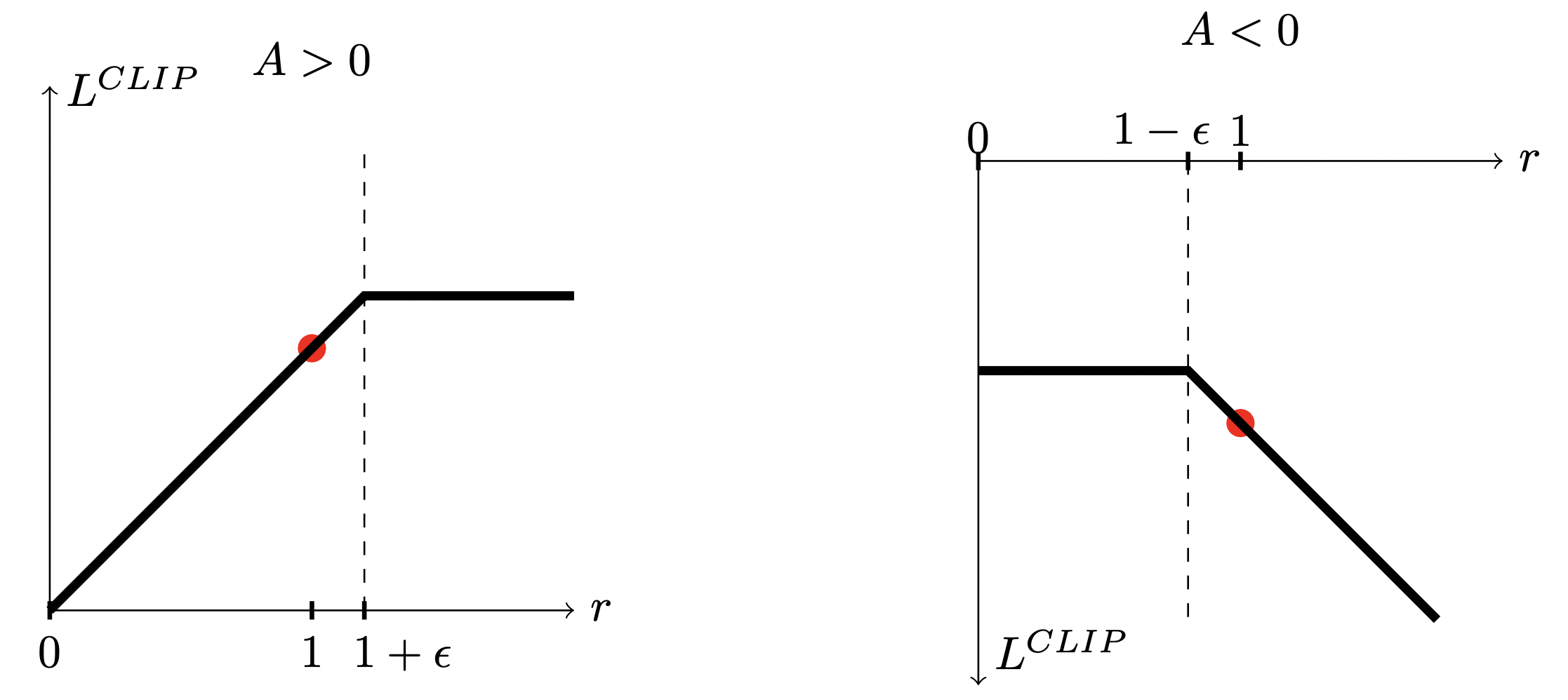
만약 \(\hat{A}_t>0\) 라면, 상태 \(s_t\)에서 행동 \(a_t\)를 취할 확률을 높여주는 방향으로 policy를 업데이트하게 된다. 따라서 \(r_t \left( \theta \right)\)이 1보다 커지게 된다. 이때, \(\operatorname{clip}\)은 \(r_t \left( \theta \right)\)이 \(1+\epsilon\) 까지만 커지도록 만들어준다.

반대로 만약 \(\hat{A}_t<0\) 라면, 상태 \(s_t\)에서 행동 \(a_t\)를 취할 확률을 낮춰주는 방향으로 policy를 업데이트한다. 즉, \(r_t \left( \theta \right)\)이 1보다 작아지게 된다. 이때, \(\operatorname{clip}\)은 \(r_t \left( \theta \right)\)이 \(1-\epsilon\) 까지만 작아지게 만들어준다.

16.2.2. 상태 가치 네트워크 및 엔트로피 보너스를 포함한 최종 목적 함수

Clipped surrogate objective는 정책 네트워크를 위한 목적 함수이다. 그리고 그 안에 있는 \(\hat{A}_t\)를 결정하는 다양한 방법이 있으며, 대부분 상태 가치 네트워크를 필요로 한다. 우리가 공부했던 \(n\)-step return과 GAE 중 아무거나 사용해도 된다. 논문에서 소개하는 advantage에 대한 추정량은 다음과 같다.

\[ \hat{A}_{t} = \delta_{t} + (\gamma\lambda)\delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\delta_{T-1}, \quad \quad (5) \]

\[ \text{where} \quad \delta_t=r_t+\gamma V(s_{t+1}) - V(s_t). \quad \quad (6) \]

\(\lambda=1\)일 때를 살펴보면 조금 와닿는다.

\[ \hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + \cdots + \gamma^{T- t +1}r_{T-1}+\gamma^{T-t} V(S_T) \]

우리가 아는 advantage \(A_t = Q(s_t, a_t) - V(s_t)\)과 식 \((6)\)을 비교해보면 \(-V(s_t)\)는 동일하게 갖고 있으며, 나머지 텀 \(r_{t} + \gamma r_{t+1} + \cdots + \gamma^{T-t+1}r_{T-1} + \gamma^{T-t} V(S_T)\)는 \(Q(s_t, a_t)\)를 추정량이다. 이 논문에서 제안하는 전체 목적 함수는 다음과 같다.

\[ L_{t}^{\text{CLIP}+\text{VF}+\text{S}}\left( \theta \right) = \hat{\mathbb{E}}_t \left[ L_t^{\text{CLIP}} \left( \theta \right) -c_{1}L_{t}^{\text{VF}}\left( \theta \right) + c_{2} S\left[\pi_{\theta}\right]\left( s_{t} \right)\right], \quad \quad (7) \]

이때 \(L_t^{\text{VF}} \left( \theta \right) = \left( V_{\theta} \left( s_{t} \right) - V_{t}^{\text{targ}} \right)^{2}\)으로 가치 함수 approximator를 훈련시키기 위한 텀이다. \(V_{t}^{\text{targ}}\)은 return이 될 수도 있고 \(n\)-step return이 될 수도 있다. 주로 return을 사용한다. \(S\left[\pi_{\theta} \right] \left( s_t \right)\)은 entropy bonus으로서 exploration을 하게 만들어주는 텀이다. 엔트로피에 관한 내용은 다음 주제인 SAC에서 더 자세히 알아볼 예정이다. 마지막으로 \(c_1, c_2\)는 각 텀에 대한 가중치이다.

---

16.2.3. 알고리즘

논문에서 소개하는 PPO 알고리즘은 다음과 같다. \(N\)개의 policy가 각각 병렬적으로 환경과 \(T\)번 상호작용하여 \(NT\)개의 경험 데이터 획득하고, 이 경험 데이터들을 사용하여 목적 함수 최적화한다는 내용이다.

Note

공부 목적으로는 병렬 환경을 사용하지 않고 \(N=1\)의 경우만 구현하면 좋지만, 아쉽게도 PPO 알고리즘은 \(N=1\)일 때 거의 잘 작동하지 않는다. 1개의 정책이 1개의 환경과 상호작용하여 얻은 \(T\)개의 데이터가 서로 너무 correlated 되어 있기 때문에 네트워크가 해당 데이터에 쉽게 과적합되기 때문이다. 동일한 파라미터를 갖는 \(N\)개의 정책으로 서로 다르게 초기화된 \(N\)개의 환경과 상호작용하여 얻은 데이터들은 상대적으로 correlated가 덜 되어 있기 때문에 PPO 등 on-policy 알고리즘 성능 향상에 거의 필수적이다.

---

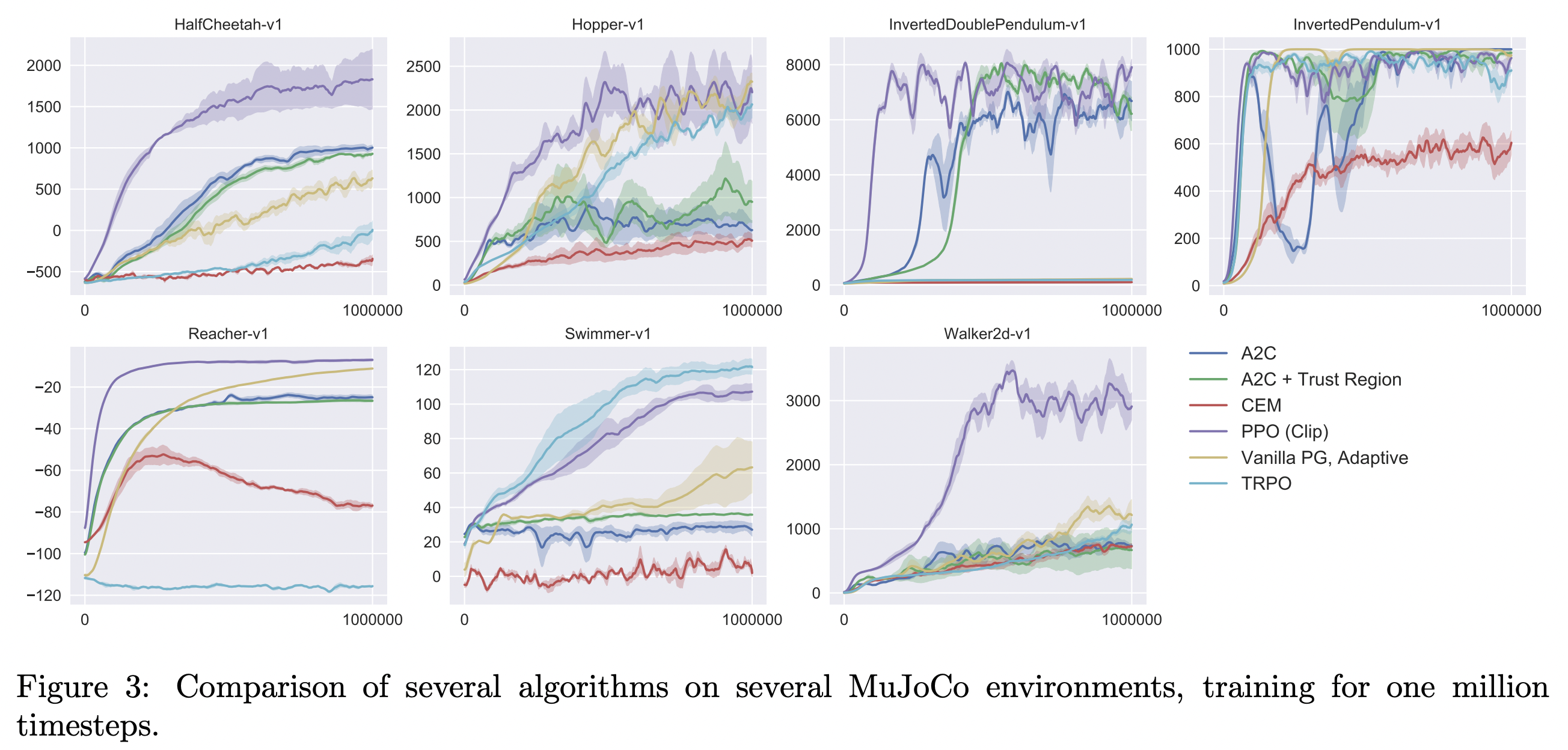
16.3. Experiment

PPO 논문에서는 다음과 같은 세팅에 대해서 실험을 진행하였다.

• HalfCheetah, Hopper, InvertedDoublePendulum, InvertedPendulum, Reacher, Swimmer, Walker2d, all “-v1”, OpenAI Gym.

• Policy network: a MLP with two hidden layers of 64 units, tanh nonlinearities, outputting the mean of a Gaussian distribution, with variable standard deviations.

• No parameter sharing between policy and value function

• No entropy bonus

• Train for 1 million timesteps

• \(\gamma=0.99, \lambda=0.95\)

---

다음 장에서는 PPO를 직접 구현해보도록 할 것이다.