REINFORCE 구현
Contents
8. REINFORCE 구현#
8.1. Gymnaisum 사용법#
먼저 강화학습 코딩이 처음인 분들에게는 에이전트가 환경과 상호작용하는 것부터 어떻게 구현해야 할지 막막할 것이다. Gymnaisum은 다양한 연습용 환경을 제공하고 있으며, 강화학습 연구자들에게 환경을 구현하기 위한 일종의 약속 (convention)을 제공하고 있다. 이번 절에서 Gymnaisum에서 제공하고 있는 CartPole 환경을 사용해볼 것이다.
먼저 실습에 사용할 라이브러리들을 모두 임포트 하자.
import random
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
import gymnasium as gym
import matplotlib.pyplot as plt
from torch.distributions import Normal
gymnasium.make('환경이름')을 통해 환경을 불러올 수 있다. Gymnasium에서 제공하는 환경의 목록은 Gymnasium의 공식 문서에 잘 나와 있다.
env = gym.make('CartPole-v1')
환경 초기화는 env.reset() 메서드를 사용하여 할 수 있다. 초기 상태 \(s_0 \sim \rho_0\)에 대응하는 코드이다. 이 메서드를 호출하면 환경의 초기 상태와 주로 학습에 사용되지는 않지만 사용자가 알면 좋은 추가 정보를 반환해준다.
s, info = env.reset()
print("Initial state is: ", s)
print("Information: ", info)
Initial state is: [-0.03563095 0.04310689 -0.04884567 -0.01530201]
Information: {}
환경의 상태를 관찰하였으니, 아무 행동을 뽑아서 환경에 행동을 취해보자. env.action_space.sample()은 행동 공간에서 임의의 행동 하나를 반환해주는 메서드이다. 다음으로 env.step(action)을 통해 환경에 행동을 취할 수 있다. env.step(action)은 5-tuple인 (s_prime, r, terminated, truncated, info)을 반환해준다.
s_prime: 다음 상태r: 보상terminated: 환경이 종료 조건에 의해 종료되었는지 여부truncated: 환경이 최대 상호작용 횟수에 도달하여 종료되었는지 여부info: 추가 정보
# Choose a random action
a = env.action_space.sample()
# Take the action
s_prime, r, terminated, truncated, info = env.step(a)
print("Next state: ", s_prime)
print("Reward: ", r)
print("Is terminated? ", terminated)
print("Is truncated? ", truncated)
print("Information: ", info)
Next state: [-0.03476881 -0.15128176 -0.04915171 0.26157826]
Reward: 1.0
Is terminated? False
Is truncated? False
Information: {}
Note
terminated와 truncated은 둘 다 환경이 종료되었는지 여부를 반환해준다. 단, terminated은 종료 조건에 의해 환경이 종료되었을 때 True를 반환한다. 종료 조건의 예시는 주로 에이전트가 목적을 달성했거나, 사망이나 붕괴 등 돌이킬 수 없는 상태에 빠졌을 경우를 의미한다. truncated은 주로 환경의 종료 조건이 따로 없는 경우에만 의미가 있다. 로봇 통제와 같은 무한히 상호작용할 수 있는 환경의 경우, 실제 구현에서는 평생 상호작용할 수 없으니 1000회 정도 상호작용 후 환경을 마친다. 이처럼 최대 상호작용 횟수에 도달하여 환경이 종료된 경우 truncated와 True를 반환한다
위의 내용을 종합하면, 한 에피소드 진행은 다음과 같이 구현한다.
s, terminated, truncated, ret = env.reset(), False, False, 0
while not (terminated or truncated):
a = env.action_space.sample()
s_prime, r, terminated, truncated, _ = env.step(a)
ret += r
s = s_prime
print("Return: ", ret)
Return: 19.0
보통 환경 초기화는 무작위성을 포함하고 있어서 reset() 메서드를 호출할 때마다 반환되는 초기 상태의 값이 달라진다.
한편, 연구자의 입장으로서 어떤 두 알고리즘을 비교할 때, 두 알고리즘이 학습 동안 마주할 환경의 초기 상태들을 완전히 동일하게 통제해줘야 할 것이다.
이는 reset() 메서드에 seed 인자를 넘겨줘서 가능하다. 단, 환경이 정의되고 가장 처음 초기화 될 때만 seed 인자를 넘겨줘야 한다. 다음 코드는 환경이 정의된 후 최초 초기화에서만 seed 인자를 넘겨주었다. 아래 코드는 몇 번을 돌려도, 커널을 재시작해도 같은 값을 반환할 것이다.
seed = 0
env = gym.make('CartPole-v1')
s, info = env.reset(seed=seed)
print(s)
s, info = env.reset()
print(s)
s, info = env.reset()
print(s)
s, info = env.reset()
print(s)
s, info = env.reset()
print(s)
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
[0.03132702 0.04127556 0.01066358 0.02294966]
[ 0.0043625 0.04350724 0.03158535 -0.04972615]
[ 0.03574043 -0.04664144 0.02296554 -0.03243444]
[ 0.03631789 0.00414612 -0.02002881 -0.00773128]
한편, 모든 초기화 때 seed 인자를 넘겨주면 다음과 같이 모든 초기 상태 값이 같아지게 된다. 이렇게 작성한 코드에 에이전트를 학습시키면 에이전트는 매번 똑같은 초기 상태에 대해서만 학습을 하기 때문에 이후에 새로운 초기 상태를 관찰하면 환경을 잘 제어하지 못할 것이다.
seed = 0
env = gym.make('CartPole-v1')
s, info = env.reset(seed=seed)
print(s)
s, info = env.reset(seed=seed)
print(s)
s, info = env.reset(seed=seed)
print(s)
s, info = env.reset(seed=seed)
print(s)
s, info = env.reset(seed=seed)
print(s)
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
[ 0.01369617 -0.02302133 -0.04590265 -0.04834723]
8.2. 이산 행동 공간#
8.2.1. 정책 네트워크 구현#
다음으로 정책 네트워크를 정의해보자. 정책은 주어진 상태 \(s\)에서 행동 \(a\)를 취한 조건부 확률 \(\text{Pr}\left[A=a|S=s \right]\)이다. 각 상태 \(s\)마다 조건부 확률 분포가 정의되어야 하므로 정책 네트워크는 상태를 입력 받는다. 그리고 행동에 대한 확률 분포이기 때문에 각 행동에 확률을 부여해야 한다.
CartPole 환경은 4차원 행동을 입력 받고 2가지 행동 중 선택하는 이산 행동 공간을 가지기 때문에 4차원 벡터를 입력 받고 2차원 벡터를 출력하는 다층퍼셉트론 (MLP)로 정의하되, 출력이 확률 분포로 해석할 수 있도록 출력에 softmax 함수를 씌울 것이다. 이 MLP 나중에 다양한 실험을 위해서 다소 일반적으로 코드를 짰다. 일반적이라는 의미는 사용자의 수요에 맞게 히든레이어 개수 및 노드 수를 조정할 수 있고 활성화 함수도 설정할 수 있도록 만들었다.
class MLPDiscretePolicy(nn.Module):
def __init__(self, state_dim, action_dim, hidden_dims=(512, ), activation_fn=F.relu):
super(MLPDiscretePolicy, self).__init__()
self.input_layer = nn.Linear(state_dim, hidden_dims[0])
self.hidden_layers = nn.ModuleList()
for i in range(len(hidden_dims) - 1):
hidden_layer = nn.Linear(hidden_dims[i], hidden_dims[i+1])
self.hidden_layers.append(hidden_layer)
self.output_layer = nn.Linear(hidden_dims[-1], action_dim)
self.activation_fn = activation_fn
def forward(self, s):
s = self.activation_fn(self.input_layer(s))
for hidden_layer in self.hidden_layers:
s = self.activation_fn(hidden_layer(s))
prob = F.softmax(self.output_layer(s), dim=-1)
return prob
정책 네트워크를 다음과 같이 선언할 수 있다.
env = gym.make('CartPole-v1')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
hidden_dims = (128, 128)
activation_fn = F.relu
policy = MLPDiscretePolicy(state_dim, action_dim, hidden_dims, activation_fn)
policy
MLPDiscretePolicy(
(input_layer): Linear(in_features=4, out_features=128, bias=True)
(hidden_layers): ModuleList(
(0): Linear(in_features=128, out_features=128, bias=True)
)
(output_layer): Linear(in_features=128, out_features=2, bias=True)
)
정책 네트워크에 상태 하나를 입력하면 다음과 같이 출력된다. 결과로 나온 벡터의 각 원소는 각 행동을 취할 확률로 해석할 수 있다.
s, _ = env.reset()
s = torch.as_tensor(s, dtype=torch.float)
policy(s)
tensor([0.5117, 0.4883], grad_fn=<SoftmaxBackward0>)
정책 네트워크로 만든 확률 분포에서 행동을 샘플링은 다음과 같이 할 수 있다.
prob = policy(s)
a = torch.multinomial(prob, num_samples=1)
print("Selected action : ", a.item())
Selected action : 1
8.2.2. 에이전트 구현#
정책 네트워크가 준비되었으니 REINFORCE 에이전트를 만들어보자. REINFORCE 에이전트는 총 4개 메서드가 있다.
__init__(): 에이전트 클래스가 입력 받을 하이퍼파라미터를 입력 받고 여러가지 초기화를 수행한다.act(): 환경과의 상호작용을 위한 메서드로서 상태 하나를 입력 받아 행동을 출력한다.learn(): 에이전트가 갖고 있는 네트워크들을 업데이트해준다.process(): 환경과의 매 상호작용마다 수행할 메서드이다. 주로 transition을 버퍼에 저장하고, 특정 주기로learn()메서드를 호출한다.
이 메서드 구성은 카카오 엔터프라이즈의 강화학습 라이브러리 JORLDY를 참고하여 만들었다. 이후 구현할 알고리즘들도 동일한 메서드 구성을 갖고 있다. 알고리즘마다 각 메서드가 어떻게 구현되는지에 초점을 맞춰 비교하면 좋을 것 같다.
class REINFORCE:
def __init__(self, state_dim, action_dim, gamma=0.99, lr=0.001):
self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
self.policy = MLPDiscretePolicy(state_dim, action_dim).to(self.device)
self.gamma = gamma
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr)
self.buffer = []
@torch.no_grad()
def act(self, s, training=True):
self.policy.train(training)
s = torch.as_tensor(s, dtype=torch.float, device=self.device)
prob = self.policy(s)
a = torch.multinomial(prob, 1) if training else torch.argmax(prob, dim=-1, keepdim=True)
return a.cpu().numpy()
def learn(self):
self.policy.train()
s, a, r, _, _, _ = map(np.stack, zip(*self.buffer))
s, a, r = map(lambda x: torch.as_tensor(x, dtype=torch.float, device=self.device), [s, a, r])
a = a.long()
r = r.unsqueeze(1)
ret = torch.clone(r)
for t in reversed(range(len(ret) - 1)):
ret[t] += self.gamma * ret[t + 1]
probs = self.policy(s)
log_probs = torch.log(probs.gather(1, a.long()))
policy_loss = - (ret * log_probs).mean()
self.optimizer.zero_grad()
policy_loss.backward()
self.optimizer.step()
result = {'policy_loss': policy_loss.item()}
return result
def process(self, transition):
result = None
self.buffer.append(transition)
if transition[-1] or transition[-2]:
result = self.learn()
self.buffer = []
return result
8.2.3. 에이전트 훈련#
REINFORCE 클래스 작성을 마쳤으니 이제 환경과 상호작용을 하면서 정책 네트워크를 훈련시킬 차례이다. Algorithm 7.1에서는 n_episodes번 반복문을 수행하는 것으로 나와 있지만 코드 구현에서는 환경과의 최대 상호작용 횟수 max_iterations에 도달할 때까지 학습을 수행하는 것으로 구현했다. 이는 강화학습 분야에서 일반적으로 사용되는 관습이다.
본격적인 실험에 앞서 실험의 재현성을 위하여 다음과 같이 랜덤 시드를 설정해주는 seed_all 함수를 정의해주었다. 단, seed_all 함수만으로는 gymnasium의 랜덤성을 잡을 수 없다. 반드시 위에서 이야기했던 env.reset(seed=seed)도 동반되어야만 코드가 실행될 때마다 같은 결과를 얻게 해준다 (연산 장비에 따라서는 달라질 수 있다).
def seed_all(seed):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
def evaluate(env_name, agent, seed, eval_iterations):
env = gym.make(env_name)
scores = []
for i in range(eval_iterations):
(s, _), terminated, truncated, score = env.reset(seed=seed + 100 + i), False, False, 0
while not (terminated or truncated):
a = agent.act(s, training=False)
s_prime, r, terminated, truncated, _ = env.step(a[0])
score += r
s = s_prime
scores.append(score)
env.close()
return round(np.mean(scores), 4)
env_name = 'CartPole-v1'
seed = 1
seed_all(seed)
max_iterations = 100000
eval_intervals = 5000
eval_iterations = 10
gamma = 0.99
lr = 0.001
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCE(state_dim, action_dim, gamma, lr)
logger = []
(s, _), terminated, truncated = env.reset(seed=seed), False, False
for t in range(1, max_iterations + 1):
a = agent.act(s)
s_prime, r, terminated, truncated, _ = env.step(a[0])
result = agent.process((s, a, r, s_prime, terminated, truncated))
s = s_prime
if result is not None:
logger.append([t, 'policy_loss', result['policy_loss']])
if terminated or truncated:
(s, _), terminated, truncated = env.reset(), False, False
if t % eval_intervals == 0:
score = evaluate(env_name, agent, seed, eval_iterations)
logger.append([t, 'Avg return', score])
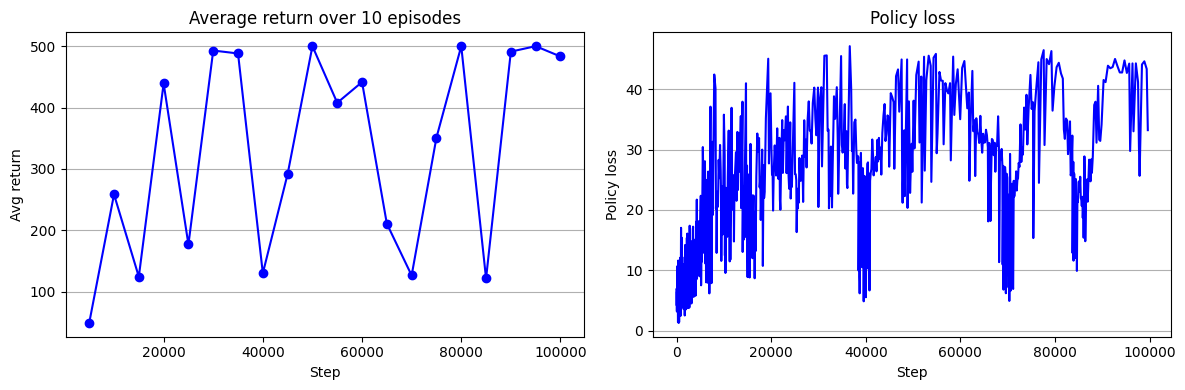
훈련 로그를 시각화해보면 다음과 같다.
logger = pd.DataFrame(logger)
logger.columns = ['step', 'key', 'value']
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(1, 2, 1)
key = 'Avg return'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'bo-')
ax.grid(axis='y')
ax.set_title("Average return over 10 episodes")
ax.set_xlabel("Step")
ax.set_ylabel("Avg return")
ax = fig.add_subplot(1, 2, 2)
key = 'policy_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Policy loss")
ax.set_xlabel("Step")
ax.set_ylabel("Policy loss")
fig.tight_layout()
plt.show()
8.3. 연속 행동 공간#
8.3.1. 환경 알아보기#
이번 절에서는 Pendulum 환경을 통해 연속 행동 공간에서 REINFORCE가 어떻게 구현되는지 알아볼 것이다.
env = gym.make('Pendulum-v1')
s, _ = env.reset()
print("The dimension of state space: ", env.observation_space.shape[0])
print("The dimension of action space: ", env.action_space.shape[0])
print("Initial state: ", s)
The dimension of state space: 3
The dimension of action space: 1
Initial state: [ 0.95943326 -0.2819358 -0.7392786 ]
8.3.2. 정책 네트워크 구현#
먼저, 정책 네트워크를 구현할 것이다. 정책 네트워크는 각 상태를 입력 받아서 행동 공간 내 모든 행동에 확률을 부여할 수 있어야 한다. 하지만, 연속 행동 공간의 경우 행동이 무수히 많아서 특정 행동에 확률을 부여할 수 없다. 연속 공간의 경우 확률 대신 확률 밀도 함수 (probability density function)를 사용한다. 우리는 상태에 따른 행동의 분포가 정규분포를 따른다고 가정할 것이다. 따라서 상태를 입력 받아 평균과 표준편차를 출력하는 정책 네트워크를 만들고, 출력된 평균과 표준편차를 따르는 정규 분포로부터 행동을 샘플링할 것이다.
class MLPGaussianPolicy(nn.Module):
def __init__(self, dim_state, dim_action, dim_hiddens=(512, ), activation_fn=F.relu):
super(MLPGaussianPolicy, self).__init__()
self.input_layer = nn.Linear(dim_state, dim_hiddens[0])
self.hidden_layers = nn.ModuleList()
for i in range(len(dim_hiddens) - 1):
hidden_layer = nn.Linear(dim_hiddens[i], dim_hiddens[i+1])
self.hidden_layers.append(hidden_layer)
self.mu_layer = nn.Linear(dim_hiddens[-1], dim_action)
self.log_std_layer = nn.Linear(dim_hiddens[-1], dim_action)
self.activation_fn = activation_fn
def forward(self, s):
s = self.activation_fn(self.input_layer(s))
for hidden_layer in self.hidden_layers:
s = self.activation_fn(hidden_layer(s))
mu = self.mu_layer(s)
log_std = torch.tanh(self.log_std_layer(s))
return mu, log_std.exp()
구현한 정책 네트워크를 선언하는 방법은 다음과 같다.
env = gym.make('Pendulum-v1')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
hidden_dims = (512, )
activation_fn = F.relu
policy = MLPGaussianPolicy(state_dim, action_dim, hidden_dims, activation_fn)
policy
MLPGaussianPolicy(
(input_layer): Linear(in_features=3, out_features=512, bias=True)
(hidden_layers): ModuleList()
(mu_layer): Linear(in_features=512, out_features=1, bias=True)
(log_std_layer): Linear(in_features=512, out_features=1, bias=True)
)
정책 네트워크로 만든 확률 분포에서 행동을 샘플링은 다음과 같이 할 수 있다.
가장 마지막에 hyperbolic tangent (torch.tanh)는 뽑힌 행동이 -1과 1사이의 값을 갖게 만들어준다.
환경마다 선택할 수 있는 행동의 최소값과 최대값이 다른데, 행동을 먼저 -1과 1사이의 값으로 만들어 준 후 행동의 범위를 알맞게 조절하는 것이 편하다.
s, _ = env.reset()
s = torch.as_tensor(s, dtype=torch.float)
mu, std = policy(s)
a = torch.normal(mu, std)
a = torch.tanh(a)
a = a.cpu().detach().numpy()
max_action = env.action_space.high
min_action = env.action_space.low
a = 0.5 * (max_action - min_action) * (a + 1) + min_action
print("Selected action: ", a)
Selected action: [-0.8433583]
Note
닫힌 구간 \([m, M]\)에서 샘플링된 행동 \(x\)를 \([-1, 1]\) 안의 값으로 바꾸는 방법은 먼저 min-max normalization을 사용해서 \([0, 1]\)의 값으로 변환한 후 2를 하고 -1을 빼주는 방식으로 진행된다. 즉,
그럼 \([-1, 1]\)으로 normalize된 값 \(x_{\text{norm}}\)을 다시 원래의 범위 \([m, M]\)로 돌리기 위해서는 다음과 같은 연산이 필요하다.
8.3.3. 에이전트 구현#
우리는 일반적인 에이전트를 구현하는 것이 목표이기 때문에 이산 행동 공간에서 만들었던 REINFORCE에 코드를 추가하는 방식을 선택할 것이다.
이를 위해서 __init__() 메서드에서 action_type 인자를 넘겨 받을 것이고, act() 메서드와 learn() 메서드에서 self.action_type 속성에 따라 행동 선택 및 확률 계산을 따로 해줄 것이다.
Policy gradient에서 \(\log \pi_\theta(a|s)\)은 생각보다 쉽게 구할 수 있다. 다음은 learn() 메서드에서 \(\log \pi_\theta(a|s)\)을 계산하는 코드이다.
mu, std = self.policy(s)
m = Normal(mu, std)
z = torch.atanh(torch.clamp(a, -1.0 + 1e-7, 1.0 - 1e-7))
log_probs = m.log_prob(z).sum(dim=-1, keepdim=True)
먼저, 우리의 MLPGaussianPolicy는 입력 상태 s에서의 평균 벡터 mu와 분산 벡터 std를 출력해준다. 네트워크가 출력하는 mu의 범위 자체에는 제한이 없다. 하지만 act() 메서드에서 tanh 활성화 함수를 취하여 샘플링된 행동을 -1과 1사이의 값으로 바꿔준다. 즉, 네트워크가 출력하는 행동의 값의 범위와 에이전트가 직접적으로 환경에 취하는 행동의 값의 범위가 다른 상태이다. -1과 1사이의 값을 원래의 값의 범위를 돌려주기 위하여 hyperbolic tangent의 역함수를 계산해주는 atanh를 사용할 것이다. 이때, atanh 함수는 -1과 1 근처에서 무한대 값을 갖기 때문에 a 변수의 값을 -1.0 + 1e-7과 1.0 - 1e-7 사이로 clip 해주었다.
그리고 \(\log \pi_\theta(a|s)\) 값은 Normal() 인스턴스 m의 log_prob() 메서드를 호출해주면 구할 수 있다. 여기서 sum() 메서드는 다차원 행동일 때 필수적이다. Pendulum-v2 환경은 일차원 행동이지만, 이후 MuJoCo의 환경들은 다차원 행동 공간을 갖는다. log_prob() 메서드는 각 차원마다의 행동의 로그 확률을 출력해준다. 각 차원의 행동들이 독립적이라고 가정하면, 모든 차원의 행동들의 확률을 곱해주어 최종적인 행동의 확률을 계산해줄 수 있을 것이다. 곱셈 연산은 로그 공간에서 덧셈이기 때문에 sum() 메서드를 사용한 것이다.
class REINFORCE:
def __init__(self, state_dim, action_dim, gamma=0.99, lr=0.001, action_type='continuous'):
self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
if action_type == 'discret':
self.policy = MLPDiscretePolicy(state_dim, action_dim).to(self.device)
else:
self.policy = MLPGaussianPolicy(state_dim, action_dim).to(self.device)
self.gamma = gamma
self.action_type = action_type
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr)
self.buffer = []
@torch.no_grad()
def act(self, s, training=True):
self.policy.train(training)
s = torch.as_tensor(s, dtype=torch.float, device=self.device)
if self.action_type == 'discrete':
prob = self.policy(s)
a = torch.multinomial(prob, 1) if training else torch.argmax(prob, dim=-1, keepdim=True)
else:
mu, std = self.policy(s)
z = torch.normal(mu, std) if training else mu
a = torch.tanh(z)
return a.cpu().numpy()
def learn(self):
self.policy.train()
s, a, r, _, _, _ = map(np.stack, zip(*self.buffer))
s, a, r = map(lambda x: torch.as_tensor(x, dtype=torch.float, device=self.device), [s, a, r])
r = r.unsqueeze(1)
ret = torch.clone(r)
for t in reversed(range(len(ret) - 1)):
ret[t] += self.gamma * ret[t + 1]
if self.action_type == 'discrete':
probs = self.policy(s)
log_probs = torch.log(probs.gather(1, a.long()))
else:
mu, std = self.policy(s)
m = Normal(mu, std)
z = torch.atanh(torch.clamp(a, -1.0 + 1e-7, 1.0 - 1e-7))
log_probs = m.log_prob(z).sum(dim=-1, keepdim=True)
policy_loss = - (ret * log_probs).mean()
self.optimizer.zero_grad()
policy_loss.backward()
self.optimizer.step()
result = {'policy_loss': policy_loss.item()}
return result
def process(self, transition):
result = None
self.buffer.append(transition)
if transition[-1] or transition[-2]:
result = self.learn()
self.buffer = []
return result
8.3.4. 에이전트 훈련#
다음으로 에이전트를 훈련시킬 것이다. CartPole에서 사용했던 코드에서 env.step() 호출 부분만 달라진다.
Gymnasium의 경우, 이산 행동 공간을 갖는 환경은 스칼라 값을 받는 반면에 연속 행동 공간을 갖는 환경은 배열을 받는다. 한편, 우리의 정책은 항상 배열을 반환해준다. 따라서
CartPole에서는 배열의 원소를 인수로 주기 위하여env.step(a[0])호출했지만,Pendulum환경에서는 에이전트가 주는 배열을 바로 인수로 넘겨준다.우리의 에이전트는 -1과 1사이의 행동을 취한다. 하지만
Gymnasium의Pendulum환경의 행동 공간은 \([-2, 2]\)이다. 따라서,env.step()에서2.0 * a를 인수로 넘겨주었다.
def evaluate(env_name, agent, seed, eval_iterations):
env = gym.make(env_name)
scores = []
for i in range(eval_iterations):
(s, _), terminated, truncated, score = env.reset(seed=seed + 100 + i), False, False, 0
while not (terminated or truncated):
a = agent.act(s, training=False)
s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
score += r
s = s_prime
scores.append(score)
env.close()
return round(np.mean(scores), 4)
env_name = 'Pendulum-v1'
seed = 1
seed_all(seed)
max_iterations = 1000000
eval_intervals = 10000
eval_iterations = 10
gamma = 0.9
lr = 0.0003
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = REINFORCE(state_dim, action_dim, gamma, lr)
logger = []
(s, _), terminated, truncated = env.reset(seed=seed), False, False
for t in range(1, max_iterations + 1):
a = agent.act(s)
s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
result = agent.process((s, a, r, s_prime, terminated, truncated))
s = s_prime
if result is not None:
logger.append([t, 'policy_loss', result['policy_loss']])
if terminated or truncated:
(s, _), terminated, truncated = env.reset(), False, False
if t % eval_intervals == 0:
score = evaluate(env_name, agent, seed, eval_iterations)
logger.append([t, 'Avg return', score])
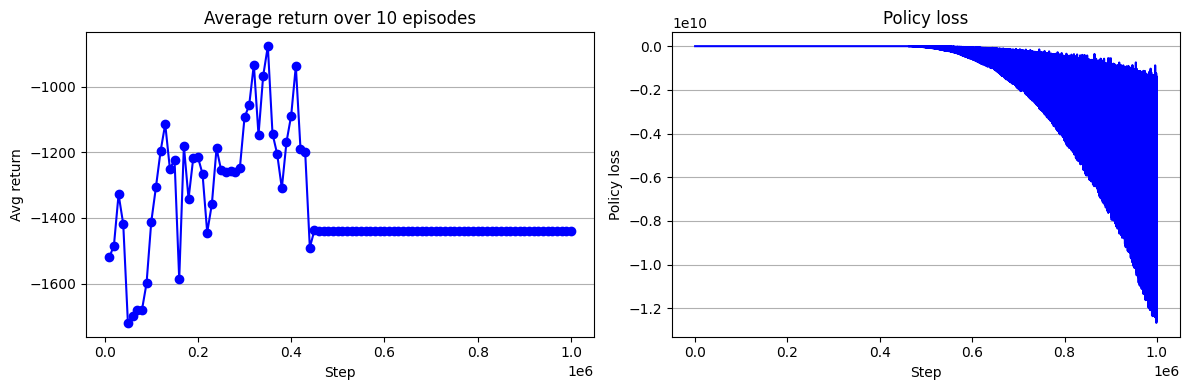
훈련 로그를 보면 다음과 같다. 결과 그래프에서 알 수 있는 것처럼 단순한 REINFORCE으로는 Pendulum 환경을 제어하기 어렵다. 이후 장에서 에이전트를 조금씩 개선하며 Pendulum 환경을 제어해보자. Policy loss 그래픠 y축 스케일을 보자. \(10^{10}\)이다 ㅋㅋ. 이러니 학습이 될리가 있냐고~~~.
이렇게 Policy loss가 큰 것은 우연이 아니다. 강화학습에서 return인 \(G_t\)값이 무진장 크다. 정의 자체가 받은 보상들을 모두 합한 것이니 클 수 밖에 없다. 그러다 보니 그레디언트 값도 커질 뿐만 아니라, 그레디언트 추정치에 대한 분산도 굉장히 크다. 다음장에서는 Baseline을 사용해서 REINFORCE를 개선해볼 것이다.
logger = pd.DataFrame(logger)
logger.columns = ['step', 'key', 'value']
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(1, 2, 1)
key = 'Avg return'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'bo-')
ax.grid(axis='y')
ax.set_title("Average return over 10 episodes")
ax.set_xlabel("Step")
ax.set_ylabel("Avg return")
ax = fig.add_subplot(1, 2, 2)
key = 'policy_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Policy loss")
ax.set_xlabel("Step")
ax.set_ylabel("Policy loss")
fig.tight_layout()
plt.show()