13. Generalized Advantage Estimation (GAE)

지난 장에서는 \(n\)-step return \(G_{t:t+n}\)을 타겟값으로 사용하여 가치 네트워크와 정책 네트워크를 학습시켜보았다. \(n\) 값을 어떻게 설정하냐에 따라서 advantage 함수에 대한 추정량의 편향과 분산의 정도가 달라졌다. \(n\)이 작을수록 추정량의 분산은 작아지고 편향은 커졌다. 반대로 \(n\)이 클수록 추정량의 분산이 커지고 편향은 작아졌다. 이 \(n\)값은 하이퍼파라미터로서 사용자가 튜닝을 통해 최적의 \(n\)을 찾아야만 한다.

그렇다면 하나의 \(n\)값만 사용하지말고 모든 \(n\)값을 고려하여 advantage 함수의 추정량을 결정하는 것은 어떨까? 모든 \(n\)값을 exponentially weighted sum하여 advantage 함수를 추정하는 방법을 generalized advantage estimation (GAE) [2]라고 부른다. GAE는 TRPO [3], PPO [4] 등 유명 알고리즘들을 만드신 John Schulman 박사님의 “High-Dimensional Continuous Control Using Generalized Advantage Estimation” 논문에서 소개된 기법이다. 논문에서는 GAE를 TRPO 알고리즘에 적용하긴 하지만 TRPO는 많이 어려운 관계로 우리는 actor-critic 알고리즘에 GAE를 적용해볼 것이다.

---

13.1. \(n\)-step return을 이용한 advantage 함수 추정

먼저, \(n\)-step return \(G_{t:t+n}\)을 다시 적어보자.

\[G_{t:t+n} = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots + \gamma^{n-1} r_{t+n-1} + \gamma^{n} V_{\phi}(s_{t+n}).\]

이 값은 policy gradient theorem (6.2)에서 행동가치함수 \(Q^{\pi}(s_t, a_t)\)의 추정치로 사용된다. 한편, advantage 함수의 정의는 행동가치함수에서 상태가치함수를 빼준 것이었다. 즉, 주어진 정책 \(\pi\)에 대해서 advantage 함수는 다음과 같이 정의된다.

\[A^{\pi}(s,a):= Q^{\pi}(s, a) - V^{\pi}(s), \; \text{for all } \; s \in \mathcal{S} \text{ and } a \in \mathcal{A}.\]

그럼, \(n\)-step return에서 슬쩍 \(V_{\phi}(s_t)\)를 차감해주면 정책 \(\pi_\theta\)에 대한 \((s_t, a_t)\)에서의 advantage 함수의 추정치가 된다. 이를 \(\hat{A}_t^{n}\)이라고 표기하면 다음과 같이 적어줄 수 있다.

\[\hat{A}_t^n := \textcolor{blue}{G_{t:t+n}} - \textcolor{red}{V_{\phi}(s_t)} = \textcolor{blue}{r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots + \gamma^{n-1} r_{t+n-1} + \gamma^{n} V_{\phi}(s_{t+n})} - \textcolor{red}{V_{\phi}(s_t)}.\]

좋았어. 이제 advantage 함수에 대한 1개의 추정치가 생겼다. 우리는 \(n=1\)부터 \(n=\infty\)까지의 \(\hat{A}_t^n\)를 모두 사용할 것이다. 그러기 위해서는 우리의 환경이 특정 조건에 의해 종료되지 않고 무한히 진행되는 환경임 (infinite horizon이라고 부름)을 가정해야 한다. 그리고 나중에 보겠지만 무한개의 추정치 \(\hat{A}_t^n\)을 가중합하게 되면 식이 굉장히 예쁘게 정리되기 때문에 실제로 무한개의 \(\hat{A}_t^n\)을 계산하거나 하진 않는다. 따라서 실제 구현에서는 환경이 infinite horizon이 아니어도 GAE를 사용할 수 있다.

---

13.2. GAE: \(\hat{A}_t^n\)의 지수적 가중합 (exponentially weighted sum)

규칙성을 파악하기 위하여 \(\hat{A}_t^n\)을 \(n=1\)부터 쭉 적어볼 것이다. 이때 유용하게 사용할 표기 하나를 다음과 같이 정의하도록 하겠다.

\[\delta_t := r_t + \gamma V_{\phi}(s_{t+1}) - V_{\phi}(s_t).\]

위 식은 \(n=1\)일 때 advantage 함수 추정치이기도 하며 보통 temporal difference error 줄여서 TD error라고 부른다. 그럼, \(\delta_t\) 표기를 사용해서 \(\hat{A}_t^n\)을 \(n=1\)부터 쭉 적어보자. 규칙성이 잘 보이도록 \(\textcolor{red}{V_{\phi}(s_t)}\)을 맨 앞에 적어주었다. 그리고 표기 편의상 가치 네트워크의 파라미터 표기 \(\phi\)도 생략했다.

\[\begin{split} \begin{matrix} \hat{A}_{t}^{1} &:= &\delta_{t} & = & -V(s_t) + r_{t}+\gamma V(s_{t+1}) \\ \hat{A}_{t}^{2} &:= &\delta_{t} + \gamma \delta_{t+1} & = & -V(s_t) + r_{t} + \gamma r_{t+1} + \gamma^2 V(s_{t+2}) \\ \hat{A}_{t}^{3} &:= &\delta_{t} + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} & = & -V(s_t) + r_{t} + \gamma r_{t+1} + \gamma^2 r_{t+2} + \gamma^{3} V(s_{t+3}) \\ \vdots & := & \vdots & = & \vdots \\ \hat{A}_{t}^{n} &:= &\sum_{l=0}^{n-1} \gamma^{l} \delta_{t+l} & = & -V(s_t) + r_{t} + \gamma r_{t+1} + \cdots + \gamma^{t+n-1}r_{t+n-1}+\gamma^{t+n} V(s_{t+n}) \\ \end{matrix} \end{split}\]

독자분들께서는 두 번째 등호가 어떻게 성립하는지 유도해보면 좋을 것 같다 (두 번째 열과 세 번째 열이 왜 같은지). 우리는 \(\hat{A}_{t}^{n}\)을 가중합하여 \((s_t, a_t)\)에서의 advantage 함수에 대한 추정치 \(\hat{A}_t\)로 사용할 것이다. 그리고 \(n\)이 작을수록 시점 \(t\)에 가까운 데이터로 구성되어 있기 때문에 이왕이면 큰 가중치를 부여하고 싶다. 특히, return \(G_t\)를 정의할 때 \(t\) 시점에서 멀리 떨어진 보상일수록 할인률 \(\gamma\)을 계속 곱해주어 미래의 보상에 대한 가중치를 낮춰준 것처럼 지수적 가중합을 사용할 것이다. 따라서 새로운 하이퍼파라미터 \(\lambda \in [0, 1]\)를 도입하여 \(\hat{A}_{t}^{n}\)을 지수적 가중합을 해줄 것이다. 즉,

\[ \hat{A}_t := (1-\lambda)\left( \hat{A}_t^{1} + \lambda \hat{A}_t^{2} + \lambda^2 \hat{A}_t^{3} + \ldots \right), \]

여기서 괄호 안은 \(\hat{A}_{t}^{n}\)을 지수적 가중합해준 것이다. 맨 앞의 \(1-\lambda\)를 곱해준 이유는 나중에 밝혀진다. 위 식을 쭉 정리해보자.

\[\begin{split} \begin{matrix} \hat{A}_t & := & (1-\lambda)\left( \hat{A}_t^{(1)} + \lambda \hat{A}_t^{(2)} + \lambda^2 \hat{A}_t^{(3)} + \ldots \right) \\ & = & (1-\lambda) \left( \delta_t +\lambda\left(\delta_t + \gamma \delta_{t+1}\right) + \lambda^2 \left(\delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} \right) +\ldots \right) \\ & = & (1-\lambda) \left( \left(1+\lambda+\lambda^2+\ldots\right)\delta_t + \gamma \lambda \left(1 +\lambda+\lambda^2+\ldots\right)\delta_{t+1} + \gamma^2 \lambda^2 \left(1 +\lambda+\lambda^2+\ldots\right)\delta_{t+2} + \ldots \right) \\ & = & \left( \delta_t + \gamma \lambda \delta_{t+1} + \gamma^2 \lambda^2 \delta_{t+2} + \ldots \right) \\ & = & \sum_{l=0}^{\infty} (\gamma\lambda)^l \delta_{t+l} \end{matrix} \end{split}\]

두 번째 등호의 우변은 각 \(\hat{A}_{t}^{n}\)들을 \(\delta_t\)텀들을 사용하여 적어준 것이고, 세 번째 등호는 그냥 \(\delta_t\)끼리 모아서 정리한 것이다. 네 번째 등호는 기하급수 공식인 \(\sum_{k=1}^{\infty} r^{k-1} = \frac{1}{1-r}\)을 사용해준 것이다. 여기서 분모를 없애주기 위하여 맨 앞의 \(1-\lambda\)가 있었던 것이다. 마지막 등호를 통해 GAE \(\hat{A}_t\)는 각 시점 \(t\)에서의 TD error \(\delta_t=r_t + \gamma V_{\phi}(s_{t+1}) - V_{\phi}(s_t)\)를 지수적 가중합한 것임을 알 수 있다. 미래의 TD error일수록 \(\gamma \lambda\)를 곱해주어 가중치를 낮춰준 것이다. 따라서 우리는 모든 \(n\)-step return을 구할 필요가 없이 각 transition \((s_t, a_t, r_t, s_{t+1})\)을 사용하여 \(\delta_t\)를 계산해주고, 이들을 가중합하여 GAE를 계산할 수 있는 것이다. 물론, 실제 구현에서는 무한개를 다 더해줄 수 없기 때문에 정해진 횟수만큼만 더해주게 된다.

---

13.3. GAE actor-critic 구현

이번 장에서는 GAE를 사용한 actor-critic 알고리즘을 Pendulum-v1 환경에 적용해볼 것이다. Buffer로 그냥 리스트를 사용해도 상관 없지만 이왕이면 지난 \(n\)-step actorc-critic 구현에서 만든 RolloutBuffer()를 사용해볼 것이다. 먼저 필요한 패키지들을 불러오자

import random
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
import gymnasium as gym
import matplotlib.pyplot as plt

from collections import deque
from torch.distributions import Normal
from tqdm import tqdm

13.3.1. GAEActorCritic 클래스 구현

GAE 구현은 BatchActorCritic() 클래스에서 __init__() 메서드와 learn() 메서드만 수정해주면 된다. 먼저, __init__() 메서드에는 GAE 계산에 필요한 하이퍼파라미터인 \(\lambda\)만 추가해주면 된다. \(\lambda\) 값으로는 0.95를 제일 많이 사용한다.

class GAEActorCritic:
    def __init__(
        self,
        state_dim,
        action_dim,
        hidden_dims=(512, ),
        batch_size=32,
        activation_fn=F.relu,
        policy_lr=0.0003,
        value_lr=0.0003,
        gamma=0.99,
        lmda=0.95
    ):
        self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
        self.policy = MLPGaussianPolicy(state_dim, action_dim, hidden_dims, activation_fn).to(self.device)
        self.value = MLPStateValue(state_dim, hidden_dims, activation_fn).to(self.device)        
        self.gamma = gamma
        self.lmda = lmda
        self.batch_size = batch_size

        self.policy_optimizer = torch.optim.Adam(self.policy.parameters(), lr=policy_lr)
        self.value_optimizer = torch.optim.Adam(self.value.parameters(), lr=value_lr)
        
        self.buffer = RolloutBuffer()

다음으로 learn() 메서드이다. 타겟값을 계산하는 부분을 GAE로 바꿔주면 되며, REINFORCE에서 return \(G_t\)를 구하는 과정과 유사하게 구현된다. 그리고 GAE 논문에서는 가치 네트워크를 업데이트할 때 REINFORCE with baseline처럼 return \(G_t\)를 타겟값으로 사용한다.

    def learn(self):
        self.policy.train()
        self.value.train()
        s, a, r, s_prime, done = self.buffer.sample()
        s, a, r, s_prime, done = map(lambda x: x.to(self.device), [s, a, r, s_prime, done])
        
        # GAE 계산
        with torch.no_grad():
            delta = r + (1 - done) * self.gamma * self.value(s_prime) - self.value(s)  # \delta_t 담은 배열
            adv = torch.clone(delta)  # gae를 담을 배열
            ret = torch.clone(r) # return을 담을 배열
            for t in reversed(range(len(r) - 1)):
                adv[t] += (1 - done[t]) * self.gamma * self.lmda * adv[t + 1]
                ret[t] += (1 - done[t]) * self.gamma * ret[t + 1]

        # \pi(a|s) 로그 확률 값 계산하기
        mu, std = self.policy(s)
        m = Normal(mu, std)
        z = torch.atanh(torch.clamp(a, -1.0 + 1e-7, 1.0 - 1e-7))
        log_probs = m.log_prob(z)
        
        # 가치 네트워크 업데이트하기
        value = self.value(s)
        value_loss = F.mse_loss(value, ret)
        self.value_optimizer.zero_grad()
        value_loss.backward()
        self.value_optimizer.step()
        
        # 정책 네트워크 업데이트
        policy_loss = -(log_probs * adv).mean()
        self.policy_optimizer.zero_grad()
        policy_loss.backward()
        self.policy_optimizer.step()

        result = {'policy_loss': policy_loss.item(), 'value_loss': value_loss.item()}

        return result

이렇게만 변동 사항이 있고 나머지 코드는 이전 actor-critic 알고리즘들 구현과 동일하다. 코드를 쭉 나열하도록 하겠다.

class RolloutBuffer:
    def __init__(self):
        self.buffer = list()

    def store(self, transition):
        self.buffer.append(transition)

    def sample(self):
        s, a, r, s_prime, done = map(np.array, zip(*self.buffer))
        self.buffer.clear()
        return (
            torch.FloatTensor(s),
            torch.FloatTensor(a),
            torch.FloatTensor(r).unsqueeze(1),
            torch.FloatTensor(s_prime),
            torch.FloatTensor(done).unsqueeze(1)
        )

    @property
    def size(self):
        return len(self.buffer)

13.3.2. 정책 네트워크 및 상태 가치 네트워크 구현

class MLPGaussianPolicy(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dims=(512, ), activation_fn=F.relu):
        super(MLPGaussianPolicy, self).__init__()
        self.input_layer = nn.Linear(state_dim, hidden_dims[0])
        self.hidden_layers = nn.ModuleList()
        for i in range(len(hidden_dims) - 1):
            hidden_layer = nn.Linear(hidden_dims[i], hidden_dims[i + 1])
            self.hidden_layers.append(hidden_layer)
        self.mu_layer = nn.Linear(hidden_dims[-1], action_dim)
        self.log_std_layer = nn.Linear(hidden_dims[-1], action_dim)
        self.activation_fn = activation_fn

    def forward(self, x):
        x = self.activation_fn(self.input_layer(x))
        for hidden_layer in self.hidden_layers:
            x = self.activation_fn(hidden_layer(x))

        mu = self.mu_layer(x)
        log_std = torch.tanh(self.log_std_layer(x))

        return mu, log_std.exp()


class MLPStateValue(nn.Module):
    def __init__(self, state_dim, hidden_dims=(512, ), activation_fn=F.relu):
        super(MLPStateValue, self).__init__()
        self.input_layer = nn.Linear(state_dim, hidden_dims[0])
        self.hidden_layers = nn.ModuleList()
        for i in range(len(hidden_dims) - 1):
            hidden_layer = nn.Linear(hidden_dims[i], hidden_dims[i + 1])
            self.hidden_layers.append(hidden_layer)
        self.output_layer = nn.Linear(hidden_dims[-1], 1)
        self.activation_fn = activation_fn

    def forward(self, x):
        x = self.activation_fn(self.input_layer(x))
        for hidden_layer in self.hidden_layers:
            x = self.activation_fn(hidden_layer(x))
        x = self.output_layer(x)

        return x

13.3.3. GAE actor-critic 에이전트 구현

class GAEActorCritic:
    def __init__(
        self,
        state_dim,
        action_dim,
        hidden_dims=(512, ),
        batch_size=32,
        activation_fn=F.relu,
        policy_lr=0.0003,
        value_lr=0.0003,
        gamma=0.99,
        lmda=0.95
    ):
        self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
        self.policy = MLPGaussianPolicy(state_dim, action_dim, hidden_dims, activation_fn).to(self.device)
        self.value = MLPStateValue(state_dim, hidden_dims, activation_fn).to(self.device)        
        self.gamma = gamma
        self.lmda = lmda
        self.batch_size = batch_size

        self.policy_optimizer = torch.optim.Adam(self.policy.parameters(), lr=policy_lr)
        self.value_optimizer = torch.optim.Adam(self.value.parameters(), lr=value_lr)
        
        self.buffer = RolloutBuffer()

    @torch.no_grad()
    def act(self, s, training=True):
        self.policy.train(training)

        s = torch.as_tensor(s, dtype=torch.float, device=self.device)
        mu, std = self.policy(s)
        z = torch.normal(mu, std) if training else mu
        action = torch.tanh(z)

        return action.cpu().numpy()
    
    def learn(self):
        self.policy.train()
        self.value.train()
        s, a, r, s_prime, done = self.buffer.sample()
        s, a, r, s_prime, done = map(lambda x: x.to(self.device), [s, a, r, s_prime, done])
        
        # GAE 계산
        with torch.no_grad():
            delta = r + (1 - done) * self.gamma * self.value(s_prime) - self.value(s)  # \delta_t 담은 배열
            adv = torch.clone(delta)  # gae를 담을 배열
            ret = torch.clone(r) # return을 담을 배열
            for t in reversed(range(len(r) - 1)):
                adv[t] += (1 - done[t]) * self.gamma * self.lmda * adv[t + 1]
                ret[t] += (1 - done[t]) * self.gamma * ret[t + 1]

        # \pi(a|s) 로그 확률 값 계산하기
        mu, std = self.policy(s)
        m = Normal(mu, std)
        z = torch.atanh(torch.clamp(a, -1.0 + 1e-7, 1.0 - 1e-7))
        log_probs = m.log_prob(z).sum(dim=-1, keepdim=True)
        
        # 가치 네트워크 업데이트하기
        value = self.value(s)
        value_loss = F.mse_loss(value, ret)
        self.value_optimizer.zero_grad()
        value_loss.backward()
        self.value_optimizer.step()
        
        # 정책 네트워크 업데이트
        policy_loss = -(log_probs * adv).mean()
        self.policy_optimizer.zero_grad()
        policy_loss.backward()
        self.policy_optimizer.step()

        result = {'policy_loss': policy_loss.item(), 'value_loss': value_loss.item()}

        return result
    
    def step(self, transition):
        result = None
        self.buffer.store(transition)
        if self.buffer.size >= self.batch_size:
            result = self.learn()

        return result
        

---

13.3.4. GAE actor-critic 에이전트 훈련

def evaluate(env_name, agent, seed, eval_iterations):
    env = gym.make(env_name)
    scores = []
    for i in range(eval_iterations):
        (s, _), terminated, truncated, score = env.reset(seed=seed + 100 + i), False, False, 0
        while not (terminated or truncated):
            a = agent.act(s, training=False)
            s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
            score += r
            s = s_prime
        scores.append(score)
    env.close()
    return round(np.mean(scores), 4)

def seed_all(seed):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.benchmark = False
    torch.backends.cudnn.deterministic = True

env_name = 'Pendulum-v1'

seed = 1
seed_all(seed)
hidden_dims = (64, 64, )
max_iterations = 1000000
eval_intervals = 10000
eval_iterations = 10
batch_size = 64
activation_fn = torch.tanh
gamma = 0.90
lmda = 0.7

env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = GAEActorCritic(
    state_dim,
    action_dim,
    hidden_dims=hidden_dims,
    activation_fn=activation_fn,
    batch_size=batch_size,
    gamma=gamma,
    lmda=lmda
)

logger = []
(s, _), terminated, truncated = env.reset(seed=seed), False, False
for t in tqdm(range(1, max_iterations + 1)):
    a = agent.act(s)
    s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
    result = agent.step((s, a, r, s_prime, terminated))
    s = s_prime
    
    if result is not None:
        logger.append([t, 'policy_loss', result['policy_loss']])
        logger.append([t, 'value_loss', result['value_loss']])
    
    if terminated or truncated:
        (s, _), terminated, truncated = env.reset(), False, False
        
    if t % eval_intervals == 0:
        score = evaluate(env_name, agent, seed, eval_iterations)
        logger.append([t, 'Avg return', score])

100%|██████████| 1000000/1000000 [09:20<00:00, 1785.20it/s]

아래는 결과 학습 곡선이다.

logger = pd.DataFrame(logger)
logger.columns = ['step', 'key', 'value']

fig = plt.figure(figsize=(12, 4))

ax = fig.add_subplot(1, 3, 1)
key = 'Avg return'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Average return over 10 episodes")
ax.set_xlabel("Step")
ax.set_ylabel("Avg return")

ax = fig.add_subplot(1, 3, 2)
key = 'policy_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Policy loss")
ax.set_xlabel("Step")
ax.set_ylabel("Policy loss")

ax = fig.add_subplot(1, 3, 3)
key = 'value_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Value loss")
ax.set_xlabel("Step")
ax.set_ylabel("Value loss")

fig.tight_layout()
plt.show()

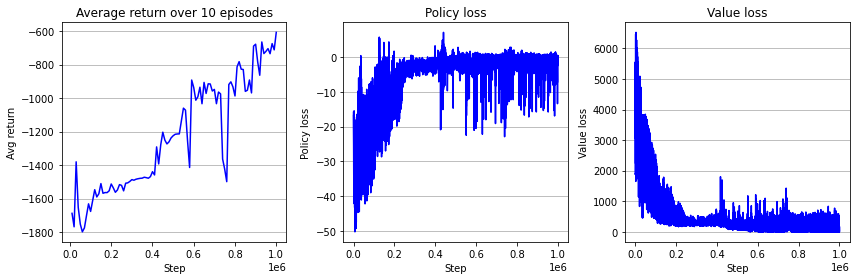
오늘 구현한 GAE를 이용하는 actor-critic 알고리즘은 이론을 구현해보는 데 초점을 맞추느라 상대적으로 쉬운 actor-critic에 필자가 GAE만 추가한 것 뿐이며 실제로는 사용되지 않는다. 하지만, 오늘 구현한 코드에서 조금만 수정하면 그 유명한 PPO 알고리즘이 된다. 하지만 PPO까지 가기 위해서는 TRPO 알고리즘을 알아야 하는데 그 이론이 조금 빡세다. 그리고 TRPO, GAE, PPO 알고리즘들은 코드 구현에 사소한 추가 디테일들이 있어야만 성능이 잘 나올 수 있다. 아직은 코드 구현 디테일에 대해서는 다루지 않았으며, 이후 PPO 알고리즘에서 알아볼 예정이다.