Online/batch actor-critic 구현
Contents
11. Online/batch actor-critic 구현#
이번 장에서는 online actor-critic과 batch actor-critic 알고리즘을 Pendulum-v1 환경에 적용해볼 것이다. Batch actor-critic에서 배치 사이즈가 \(N=1\)인 경우가 online actor-critic이기 때문에 우리는 batch actor-critic을 구현하고 \(N=1\)일 때와 \(N=64\)일 때를 비교해볼 것이다. 지난 구현들과 겹치는 코드들은 따로 설명하지 않을 것이다. 먼저 필요한 패키지의 모듈들을 불러오자
import random
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
import gymnasium as gym
import matplotlib.pyplot as plt
from torch.distributions import Normal
11.1. 정책 네트워크 및 상태 가치 네트워크 구현#
REINFORCE with baseline에서 사용한 네트워크와 동일하다.
class MLPGaussianPolicy(nn.Module):
def __init__(self, state_dim, action_dim, hidden_dims=(512, ), activation_fn=F.relu):
super(MLPGaussianPolicy, self).__init__()
self.input_layer = nn.Linear(state_dim, hidden_dims[0])
self.hidden_layers = nn.ModuleList()
for i in range(len(hidden_dims) - 1):
hidden_layer = nn.Linear(hidden_dims[i], hidden_dims[i + 1]);
self.hidden_layers.append(hidden_layer)
self.mu_layer = nn.Linear(hidden_dims[-1], action_dim)
self.log_std_layer = nn.Linear(hidden_dims[-1], action_dim)
self.activation_fn = activation_fn
def forward(self, x):
x = self.activation_fn(self.input_layer(x))
for hidden_layer in self.hidden_layers:
x = self.activation_fn(hidden_layer(x))
mu = self.mu_layer(x)
log_std = torch.tanh(self.log_std_layer(x))
return mu, log_std.exp()
class MLPStateValue(nn.Module):
def __init__(self, state_dim, hidden_dims=(512, ), activation_fn=F.relu):
super(MLPStateValue, self).__init__()
self.input_layer = nn.Linear(state_dim, hidden_dims[0])
self.hidden_layers = nn.ModuleList()
for i in range(len(hidden_dims) - 1):
hidden_layer = nn.Linear(hidden_dims[i], hidden_dims[i + 1])
self.hidden_layers.append(hidden_layer)
self.output_layer = nn.Linear(hidden_dims[-1], 1)
self.activation_fn = activation_fn
def forward(self, x):
x = self.activation_fn(self.input_layer(x))
for hidden_layer in self.hidden_layers:
x = self.activation_fn(hidden_layer(x))
x = self.output_layer(x)
return x
11.2. Batch actor-critic 구현#
아래는 actor-critic 알고리즘을 구현한 것이다. 메서드별 상세한 설명은 클래스 정의 아래에 적어 놓았다.
class ActorCritic:
def __init__(
self,
state_dim,
action_dim,
hidden_dims=(512, ),
batch_size=32,
activation_fn=F.relu,
policy_lr=0.0003,
value_lr=0.0003,
gamma=0.99,
):
self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
self.policy = MLPGaussianPolicy(state_dim, action_dim, hidden_dims, activation_fn).to(self.device)
self.value = MLPStateValue(state_dim, hidden_dims, activation_fn).to(self.device)
self.gamma = gamma
self.batch_size = batch_size
self.policy_optimizer = torch.optim.Adam(self.policy.parameters(), lr=policy_lr)
self.value_optimizer = torch.optim.Adam(self.value.parameters(), lr=value_lr)
self.buffer = []
@torch.no_grad()
def act(self, s, training=True):
self.policy.train(training)
s = torch.as_tensor(s, dtype=torch.float, device=self.device)
mu, std = self.policy(s)
z = torch.normal(mu, std) if training else mu
action = torch.tanh(z)
return action.cpu().numpy()
def learn(self):
self.policy.train()
self.value.train()
s, a, r, s_prime, _, terminated = map(np.stack, zip(*self.buffer))
s, a, r, s_prime, done = map(
lambda x: torch.as_tensor(x, dtype=torch.float, device=self.device),
[s, a, r, s_prime, terminated]
)
r = r.unsqueeze(1)
done = done.unsqueeze(1)
# \pi(a|s) 로그 확률 값 계산하기
mu, std = self.policy(s)
m = Normal(mu, std)
z = torch.atanh(torch.clamp(a, -1.0 + 1e-7, 1.0 - 1e-7))
log_probs = m.log_prob(z).sum(dim=-1, keepdim=True)
# 가치 네트워크 업데이트하기
value = self.value(s)
td_target = r + (1 - done) * self.gamma * self.value(s_prime) # r + gamma V_{\phi}(s')
value_loss = F.mse_loss(value, td_target.detach()) # td_target은 상수로 사용되기 때문에 detach() 해줘야 한다.
self.value_optimizer.zero_grad()
value_loss.backward()
self.value_optimizer.step()
# 정책 네트워크 업데이트
policy_loss = -(log_probs * (td_target - value).detach()).mean()
self.policy_optimizer.zero_grad()
policy_loss.backward()
self.policy_optimizer.step()
result = {'policy_loss': policy_loss.item(), 'value_loss': value_loss.item()}
return result
def step(self, transition):
result = None
self.buffer.append(transition)
if len(self.buffer) > self.batch_size:
result = self.learn()
self.buffer = []
return result
__init__()메서드는 몇 번의 상호작용마다 네트워크들을 업데이트할지를 결정하는batch_size인자가 추가된 것 외에는 REINFORCE with baseline과 동일하다.act()메서드도 continuous action의 경우만 구현했다는 차이가 있을 뿐 REINFORCE with baseline과 동일하다.step()메서드는 환경과 1번 상호작용할 때마다 에이전트가 하는 행동을 정의해놓은 메서드이다. REINFORCE with baseline 구현에서process()메서드에 대응하는 메서드인데, 필자의 변덕으로 인해 이름이step()으로 변경됐다. REINFORCE with baseline에서는 매 스탭마다 데이터를buffer라는 리스트에 추가해주었다. 그리고 에피소드가 종료되었다면self.learn()을 호출하여 네트워크를 업데이트해줬었다.
# REINFORCE with baseline의 process() 메서드
def process(self, transition):
result = None
self.buffer.append(transition)
if transition[-1] or transition[-2]:
result = self.learn()
self.buffer = []
return result
Batch actor-critic의 경우 매
batch_size스탭마다self.learn()을 호출해주면 된다.
# Batch actor-critic의 step() 메서드
def step(self, transition):
result = None
self.buffer.append(transition)
if len(self.buffer) > self.batch_size:
result = self.learn()
self.buffer = []
return result
learn()메서드에서는 가치 네트워크와 정책 네트워크를 업데이트할 때 사용되는 타겟값이 달라진다. REINFORCE with baseline에서는 각 시점 \(t\)에 대응하는 \(G_t\)를 계산하여 가치 네트워크와 정책 네트워크를 업데이트했다. Actor-critic 알고리즘에서는 \(G_t\) 대신 \(r_t + \gamma V_{\phi}(s_{t+1})\)을 계산한다. 이는td_target변수에 정의되어 있으며 temporal difference target이라는 뜻이다. \(t\)시점의 상태 \(s_t\)에 대한 가치 네트워크의 타겟값이 다음 시점의 상태 \(s_{t+1}\)에 의존적이기 때문에 붙여진 이름이다.
value = self.value(s)
td_target = r + (1 - done) * self.gamma * self.value(s_prime) # r + gamma V_{\phi}(s')
value_loss = F.mse_loss(value, td_target.detach()) # td_target은 상수로 사용되기 때문에 detach() 해줘야 한다.
self.value_optimizer.zero_grad()
value_loss.backward()
self.value_optimizer.step()
구현 디테일로는
td_target을 계산할 때 들어가는(1 - done)이다. 만약 다음 상태인s_prime이 마지막 상태라면, 마지막 상태 이후로는 에피소드가 진행이 되지 않기 때문에 보상을 받지 않을 것이다. 따라서 마지막 상태의 가치함수는 0이 된다. 이를 반영하기 위하여(1 - done)을 곱해주어 만약done이 True이면, 즉 에피소드가 종료되었다면 0을 곱해주어 가치함수텀을 없애주는 것이다.두 번째 구현 디테일로는
value_loss를 계산할 때, 레이블로 사용되는td_target의 경우self.value(s_prime)텀을 포함하고 있기 때문에 가치 네트워크의 파라미터가 포함되어 있다.td_target은 레이블로서 사용되는 것이고value_loss를 줄이는 데 사용되는 것이 아니기 때문에detach()메서드를 통해 그레디언트를 계산 과정을 computational graph에서 제거해준다.
정책 네트워크 또한 \((G_t - V_{\phi}(s_t)) \nabla \pi (a_t|s_t)\) 대신 \((r_t + \gamma V_{\phi}(s_{t+1}) - V_{\phi}(s_t)) \nabla \pi (a_t|s_t)\)을 통해 업데이트해준다. 마찬가지로
td_target - value는 상수로서 사용되기 때문에detach()메서드를 사용했다. 사실policy loss는policy_optimizer로만 줄이기 때문에 가치 네트워크 파라미터는 업데이트가 되지 않지만 필자는 혹시 몰라서 붙이는 편이다.
# 정책 네트워크 업데이트
policy_loss = -(log_probs * (td_target - value).detach()).mean()
self.policy_optimizer.zero_grad()
policy_loss.backward()
self.policy_optimizer.step()
11.3. Actor-critic 에이전트 훈련#
이후 코드는 REINFORCE와 REINFORCE with baseline와 동일하다. 네트워크 구조는 이전과 살짝 다른데, 나중에 구현할 PPO와 비슷하게 만들어 놓았다.
def evaluate(env_name, agent, seed, eval_iterations):
env = gym.make(env_name)
scores = []
for i in range(eval_iterations):
(s, _), terminated, truncated, score = env.reset(seed=seed + 100 + i), False, False, 0
while not (terminated or truncated):
a = agent.act(s, training=False)
s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
score += r
s = s_prime
scores.append(score)
env.close()
return round(np.mean(scores), 4)
def seed_all(seed):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
11.3.1. Batch actor-critic#
\(N=64\)일 때 batch actor-critic 훈련 코드이다. 매 64번의 상호작용마다 네트워크 업데이트가 이뤄진다.
%%time
env_name = 'Pendulum-v1'
seed = 1
seed_all(seed)
hidden_dims = (64, 64, )
max_iterations = 1000000
eval_intervals = 5000
eval_iterations = 10
batch_size = 64
gamma = 0.95
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = ActorCritic(state_dim, action_dim, hidden_dims=hidden_dims, gamma=gamma, batch_size=batch_size)
logger = []
(s, _), terminated, truncated = env.reset(seed=seed), False, False
for t in range(1, max_iterations + 1):
a = agent.act(s)
s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
result = agent.step((s, a, r, s_prime, terminated, truncated))
s = s_prime
if result is not None:
logger.append([t, 'policy_loss', result['policy_loss']])
logger.append([t, 'value_loss', result['value_loss']])
if terminated or truncated:
(s, _), terminated, truncated = env.reset(), False, False
if t % eval_intervals == 0:
score = evaluate(env_name, agent, seed, eval_iterations)
logger.append([t, 'Avg return', score])
CPU times: user 8min 48s, sys: 890 ms, total: 8min 49s
Wall time: 8min 48s
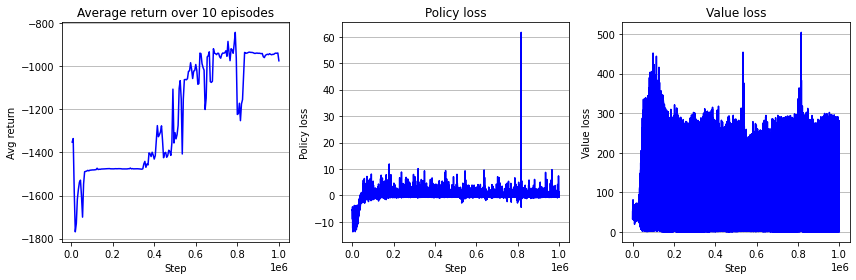
아래는 학습 결과 시각화이다. 사실 이 한 번의 실험만으로 REINFORCE with baseline이 더 좋은지 actor-critic이 더 좋은지 결정할 수는 없다. 진정한 비교를 위해서는 각 알고리즘을 적게는 5회, 중간 횟수로는 10회, 많게는 30회 돌려서 스탭당 성능의 기댓값으로 비교를 해봐야 한다.
logger = pd.DataFrame(logger)
logger.columns = ['step', 'key', 'value']
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(1, 3, 1)
key = 'Avg return'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Average return over 10 episodes")
ax.set_xlabel("Step")
ax.set_ylabel("Avg return")
ax = fig.add_subplot(1, 3, 2)
key = 'policy_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Policy loss")
ax.set_xlabel("Step")
ax.set_ylabel("Policy loss")
ax = fig.add_subplot(1, 3, 3)
key = 'value_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Value loss")
ax.set_xlabel("Step")
ax.set_ylabel("Value loss")
fig.tight_layout()
plt.show()
11.3.2. Online actor-critic#
\(N=1\)일 때 online actor-critic 훈련 코드이다. 매 스탭마다 네트워크 업데이트가 이뤄지기 때문에 학습이 끝날 때까지 시간이 많이 소요된다.
%%time
env_name = 'Pendulum-v1'
seed = 1
seed_all(seed)
hidden_dims = (64, 64, )
max_iterations = 1000000
eval_intervals = 5000
eval_iterations = 10
batch_size = 1
gamma = 0.95
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = ActorCritic(state_dim, action_dim, hidden_dims=hidden_dims, gamma=gamma, batch_size=batch_size)
logger = []
(s, _), terminated, truncated = env.reset(seed=seed), False, False
for t in range(1, max_iterations + 1):
a = agent.act(s)
s_prime, r, terminated, truncated, _ = env.step(2.0 * a)
result = agent.step((s, a, r, s_prime, terminated, truncated))
s = s_prime
if result is not None:
logger.append([t, 'policy_loss', result['policy_loss']])
logger.append([t, 'value_loss', result['value_loss']])
if terminated or truncated:
(s, _), terminated, truncated = env.reset(), False, False
if t % eval_intervals == 0:
score = evaluate(env_name, agent, seed, eval_iterations)
logger.append([t, 'Avg return', score])
CPU times: user 33min 48s, sys: 9.4 s, total: 33min 57s
Wall time: 33min 53s
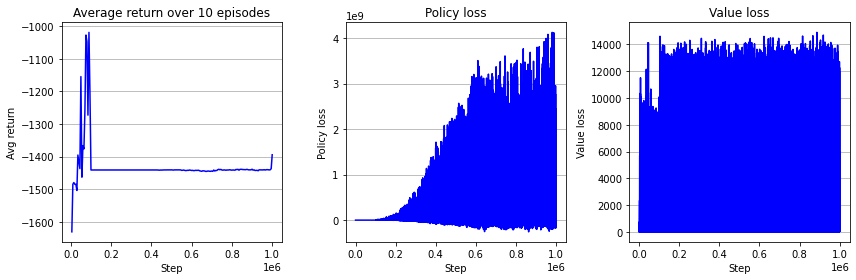
8분 밖에 소요되지 않았던 batch actor-critic과 달리 online actor-critic은 32분이 소요되었다. 매 스탭마다 그레디언트 역전파 및 파라미터 업데이트가 일어나기 때문이다. 그리고 한 번의 실험만으로 단정할 수 없지만, 같은 무작위성 아래에서 online actor-critic은 환경 제어에 완전히 실패했다. 가장 큰 이유로는 정책 네트워크와 가치 네트워크의 손실값이 발산한 것이 있을 것이다. 아무래도 데이터 1개만으로 policy gradient를 추정하다보니 추정치의 분산이 굉장히 클 것이다. 실제 그레디언트와 많이 차이나는 추정치도 있을 것이다.
logger = pd.DataFrame(logger)
logger.columns = ['step', 'key', 'value']
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(1, 3, 1)
key = 'Avg return'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Average return over 10 episodes")
ax.set_xlabel("Step")
ax.set_ylabel("Avg return")
ax = fig.add_subplot(1, 3, 2)
key = 'policy_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Policy loss")
ax.set_xlabel("Step")
ax.set_ylabel("Policy loss")
ax = fig.add_subplot(1, 3, 3)
key = 'value_loss'
ax.plot(logger.loc[logger['key'] == key, 'step'], logger.loc[logger['key'] == key, 'value'], 'b-')
ax.grid(axis='y')
ax.set_title("Value loss")
ax.set_xlabel("Step")
ax.set_ylabel("Value loss")
fig.tight_layout()
plt.show()
이것으로 actor-critic 구현을 마치도록 하겠다. 다음 주제로는 네트워크 업데이트에 사용되는 타겟값 \(G_t\) 또는 \(r_t + \gamma V_{\phi}(s_{t+1})\)의 중간 지점에 있는 \(n\)-step return과 모든 \(n\)-step return을 가중평균하는 Generalized Advantage Estimation (GAE)에 대해서 알아볼 것이다.

