Chapter 2. Background and Traditional Approaches

Graph Representation Learning Book 읽고 정리하기 시리즈 중 두 번째 이야기. 부디 완주하게 기도해주세요 !

이 책의 주된 주제는 그래프를 벡터로 표현하는 방법 Graph Representation Learning과 그래프에 딥러닝을 적용하는 방법 Deep learning on graphs 이다. 이번 챕터에서는 위 두 가지 주제를 보다 더 잘 이해하기 위한 사전지식을 배운다. 특히, 딥러닝 등장 이전에 그래프 자료구조에 사용됐던 기법들을 풀고자 하는 문제들에 따라서 알아본다.

1. 그래프 분류 를 위한 그래프 통계량 및 커널 메서드
2. 이웃 노드 중복도를 사용한 relation prediction
3. 군집화 및 커뮤니티 탐지 를 위한 Laplacian 기반의 Spectral Clustering

Chapter 2.1 Graph Statistics and Kernel Methods

대부분의 머신러닝 모델들은 벡터로 표현된 데이터를 입력값으로 받는다. 하지만 노드, 엣지, 그래프는 벡터가 아니기 때문에 머신러닝 모델에 넣어줄 수 없다. 따라서, 그래프로 표현되는 데이터를 머신러닝 모델에 사용하기 위해서는 노드든 엣지든 그래프든 먼저 벡터로 표현해야 한다. 이번 섹션에서는 먼저 노드 레벨에서 feature 또는 통계량을 뽑아내는 방법을 알아본다. 다음으로 노드 레벨 feature를 그래프 레벨 feature로 확장시키는 방법과 추가적으로 그래프 커널 방법론에 대해 알아본다.

2.1.1 Node-level Statistics and Features

이번 서브 섹션에서는 대표적인 각 노드가 갖고 있는 통계량에 대해서 알아본다.

Node Degree (차수)

주어진 그래프의 한 노드 $u$의 차수는 노드 $u$에 인접한 이웃 노드의 개수이며 $d_u$라고 표기한다. 노드 $u$의 차수 $d_u$를 인접행렬 $\mathbf{A}$로 나타내면 다음과 같다.

• $d_u=\sum\limits_{v \in V} \mathbf{A}[u, v] \quad\quad (2.1)$

인접행렬 $\mathbf{A}$의 $u$행의 각 원소를 더해주는 것이다. 인접행렬의 정의에 따라 노드 $v$가 노드 $u$와 이웃이라면 $\mathbf{A}[u,v]$ 값이 1이 된다. 반대로 노드 $v$가 노드 $u$와 이웃이 아니라면 $\mathbf{A}[u,v]$ 값이 0이다. 따라서 이를 모두 더하면 이웃 노드의 개수가 된다. 노드 차수는 오래 전부터 가장 핵심적이고 유익한 정보 중 하나였다. 하지만, 이 통계량은 노드의 중요도를 나타내기에는 조금 부족하다. 차수가 1로 동일한 두 노드가 있다고 생각해보자. 연결된 하나의 이웃 노드가 얼마나 중요하느냐에 따라서 두 노드들의 중요도도 달라질 것이다. 차수는 이를 반영해주지 못한다.

Node Centrality

해당 노드가 그래프 안에서 얼마나 중요한지를 나타낼 수 있는 통계량이다. Node Centrality는 여러 종류가 있는데, 가장 먼저 Eigenvector Centrality 에 대해서 알아보자. Eigenvector Centrality의 핵심은 이웃 노드들의 중요도로 내 중요도를 계산한다. 주어진 그래프의 한 노드 $u$의 eigenvector centrality $e_u$는 다음과 같이 정의된다.

• $e_u=\frac{1}{\lambda}\sum_{v \in V}\mathbf{A}[u, v] \; e_v,\quad \forall u \in V \quad\quad (2.2)$

식 $(2.2)$는 recursive한 성질을 갖는다. 노드 $u$의 centrality $e_u$를 구할 때 이웃 노드의 centrality $e_v$를 사용한다. 그래서 먼저 $e_v$ 값을 구하러 가보면 노드 $v$의 이웃 노드 중에 $u$가 있기 때문에 $e_v$ 값 계산에 다시 $e_u$가 필요하다. 계란이 먼저냐 닭이 먼저냐의 문제가 되버린다. 계산하기 정말 막막하지만, 사실은 굉장히 쉽게 구해진다고 한다. 각 노드들의 eigenvector centrality를 원소로 갖는 벡터 $\mathbf{e}$ 는 인접행렬 $\mathbf{A}$의 eigen-equation을 풀어서 얻을 수 있다. 즉, $\mathbf{e}$는 다음을 만족한다.

• $\lambda\mathbf{e}=\mathbf{A}\mathbf{e} \quad \quad (2.3)$

사실, 이렇게 구한 벡터가 노드들의 중요도를 나타낼 수 있다는 것이 잘 와닿지 않는다. 그래서 내 나름대로 이해하기 위한 발버둥을 쳐봤다. 다음은 eigenvector centrality에 대한 나의 고찰이다.

• 인접행렬 $\mathbf{A}$에 어떤 벡터 $\mathbf{v}$를 곱한다는 것의 의미를 살펴보자.
• 쉬운 이해를 위해 $\mathbf{v}$에는 각 노드의 가치 또는 가격이 적혀있다고 생각하자. 예를 들어, 첫 번째 노드의 가격은 1,000원, 두 번째 노드의 가격은 20,000원 이런 식으로 가격을 갖는 노드 중요도 벡터를 상상해보자.
• 인접행렬 $\mathbf{A}$의 $u$ 번 째 행은 노드 $u$의 이웃 노드에 1로 마킹한 행벡터이다.
• 그럼, $\mathbf{A} \mathbf{v}$의 $u$번 째 원소는 노드 $u$의 이웃 노드들의 가격을 모두 더한 것이다. 즉, 이웃들의 중요도를 다 더한 것이다.
  • 사실, $\mathbf{v}$를 어떻게 선택하느냐에 따라서, $\mathbf{A} \mathbf{v}$ 안의 원소들 (노드 중요도)의 크고 작음이 달라질 수 있다. 어떤 $\mathbf{v}$에 대해서는 세 번째 노드가 가장 중요했는데, 다른 $\mathbf{v}$에 대해서는 다섯 번째 노드가 가장 중요할 수도 있다는 의미이다.
  • 뿐만 아니라, $\mathbf{A} \mathbf{v}$ 벡터를 다시 중요도 벡터로 사용할 수도 있을 것이다. 그럼 다시 $\mathbf{A}$를 곱하여 중요도 벡터를 구하게 되는데, 이때도 역시 노드 중요도의 순위가 달라질 수 있다.
• 이를 대처할 수 있는 것이 eigenvector $\mathbf{e}$ 이다.
  • $A\mathbf{e}=\lambda\mathbf{e}$ 이다. 인접행렬 $\mathbf{A}$를 $n$번 곱해주면 $\lambda^n \mathbf{e}$가 된다. 상수배는 순위에 영향을 주지 않는다.

위와 같은 느낌에서 eigenvector를 중요도 벡터로 사용했을 때 얻는 이점이 많은 것 같다. 뿐만 아니라, Perron-Frobenius 이론이라는 것에 의하여 식 $(2.3)$을 풀었을 때 가장 큰 eigenvalue가 유일하게 존재하고, 대응하는 eigenvector의 원소는 모두 같은 부호를 갖는다고 한다. 따라서, 양수의 통계량을 얻을 수 있다는 이점도 있다.

책에서는 eigenvector와 그래프 랜덤 워킹 사이의 관계에 대해서도 설명하고 있다. 깊게 다루고 있지는 않아서 가벼운 마음으로 받아들였다.

• Eigenvector centrality는 그래프 안에서 무한히 많이 랜덤워킹할 때, 해당 노드에 도착한 비율 또는 해당 노드에 도착할 확률이다. (이 둘은 무한 길이의 랜덤워킹의 경우 같다.)
• $\mathbf{e}^{(0)}=(1, 1, \cdots, 1)^T$에서 시작하여 다음과 같은 power iteration을 할 때,
  • $\mathbf{e}^{(t+1)}=A\mathbf{e}^{(t)} \quad \quad (2.4)$
• $\mathbf{e}^{(1)}$은 각 원소의 degree가 된다. 이는 해당 노드를 1회 워킹만으로 도착하는 경우의 수이다.
• $\mathbf{e}^{(t)}$는 해당 노드를 $t$회 워킹으로 도착하는 경우의 수이다.

이 책에서는 eigenvector centrality 외에 betweenness centrality 와 closeness centrality도 소개한다.

• Betweenness Centrality
  • 해당 노드가 다른 두 노드 사이의 최단 경로에 있는 경우의 수
  • $c_u=\sum_{u \ne v_1 \ne v_2}\frac{\text{$v_1$과 $v_2$의 최단 경로에 u가 포함되는 횟수}}{\text{$v_1$과 $v_2$의 최단 경로의수}}$
  • (예) 대전
• Closeness Centrality
  • 해당 노드와 다른 노드 사이의 최단 경로의 평균값
  • $c_u=\frac{1}{\sum_{v \ne u} \text{$u$와 $v$사이의 최단 경로 길이}}$

The Clustering Coefficient

The clustering coefficient는 한 노드의 이웃 노드들이 얼마나 긴밀하게 연결되어 있는가를 나타낼 수 있는 척도이다. 다음 그림에서 노드 $u_1$과 $u_2$의 차수는 4로 같지만, 노드 $u_2$의 이웃 노드들은 서로 더 긴밀하게 연결되어 있음을 알 수 있다. 다양한 clustering coefficient들이 있지만, 이 책에서는 local clustering coefficient만을 소개한다.

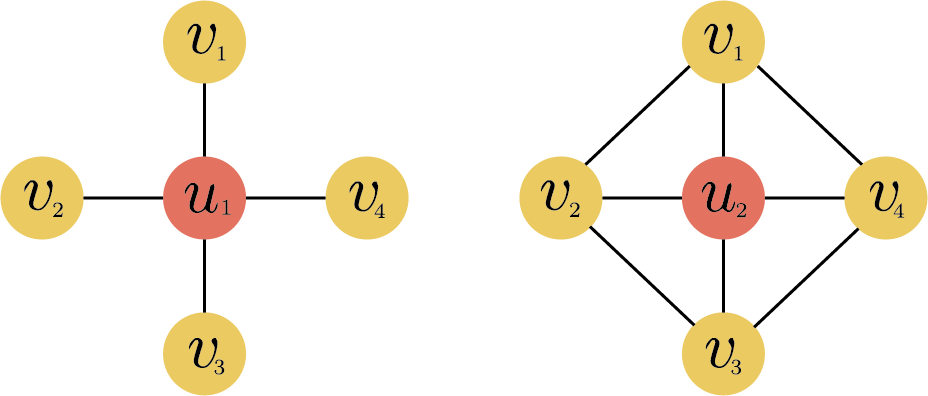
그래프 $G=(V, E)$의 한 노드 $u \in V$의 local clustering coefficient $c_u$는 다음과 같이 정의된다.

• $c_u = \frac{\mid (v_1, v_2) \in E : v_1, v_2 \in \mathcal{N}(u)\mid}{_{d_u}\mathrm{C}_2}, \quad \mathcal{N}(u)=\{v \in V:(u, v) \in E\} \quad \quad (2.5)$

$\mathcal{N}(u)$는 $u$의 이웃 노드들을 모아놓은 집합이다. $V$에 있는 노드 $v$ 중에 $(u, v)$가 $E$에 있는 애들, 즉, $u$와 연결된 노드들을 모아놓은 것이기 때문이다. $c_u$의 분자는 $u$의 이웃 노드들끼리 서로 연결된 엣지의 개수이다. 분모는 $u$의 이웃 노드들 중에서 2개를 뽑는 경우의 수이다. 따라서 $c_u$는 노드 $u$의 이웃 노드들끼리 서로 연결된 비율로 이해할 수 있다.

위의 그림에서 $u_1$의 이웃 노드들끼리는 서로 연결되어 있지 않기 때문에 $c_{u_1}=0$이 된다. $u_2$의 이웃 노드들 중에서는 $(v_1, v_2)$, $(v_2, v_3)$, $(v_3, v_4)$, $(v_4, v_1)$가 연결되어 있기 때문에 분자는 4가 되고, 분모는 $_{4}\mathrm{C}_2=6$이 되어 $c_{u_2}=2/3$이 된다. 만약, $(v_1, v_3)$과 $(v_2, v_4)$도 연결되어 있었다면 local clustering coefficient 값은 1이 되었을 것이다. 얼핏 보기에는 $(v_1, v_3)$과 $(v_2, v_4)$가 연결되어 있는 것처럼 보일 수도 있지만 $u_2$를 경유하는 상태라서 path는 있지만 서로가 이웃되어 있지는 않기 때문에 분자에 카운트되지 않는다.

Local clustering coefficient를 다른 관점에서 보면 다음과 같이 생각할 수 있다.

• $u$의 Ego 그래프에서 만들 수 있는
• $u$를 포함하는 삼각형 모양의 부분 그래프의 개수를 구해서
• 가능한 모든 삼각형 모양의 부분 그래프의 개수로 나눠준 것이다.

바로 이어서 다룰 Graphlet은 삼각형 모양의 부분 그래프 뿐만 아니라 노드 $u$ 주변에서 만들 수 있는 다양한 모양의 부분 그래프를 사용해서 노드 또는 그래프의 feature를 생성해낸다.

Closed Triangles, Ego Graphs, and Motifs

소제목에는 3개의 개념이 있다. closed triangles과 ego graph는 바로 이전에 local clustering coefficient에서 다룬 개념이다. 남은 개념은 motifs인데 책에는 설명이 너무 부실하고, 검색해도 잘 나오지 않는다. 따라서, 여기서는 motifs 대신 graphlets 이란 개념을 사용한 feature 벡터 만드는 방법을 이야기하고자 한다.

k-graphlets은 $k$개의 노드로 만들 수 있는 서로 동형이 아닌 그래프들을 모아놓은 것이다. 노드가 $k$개 있다면 서로 다른 두 엣지를 고르는 경우의 수는 $_{k}\mathrm{C}_{2}=\frac{k(k-1)}{2}$개이다. 그리고 각 경우의 수마다 엣지가 있을 수도 있고 없을 수도 있다. 따라서 $k$개의 노드로 만들 수 있는 모든 그래프의 개수는 $2^{\frac{k(k-1)}{2}}$개일 것이다. 정말 많은 개수이다. 하지만 사실 이들 중에는 노드에 부여된 인덱스를 가리고 보면 겹치는 그래프가 굉장히 많을 것이다. k-graphlets은 인덱스가 부여되지 않은 $k$개의 노드로 만들 수 있는 그래프들이라고 생각하면 된다.아래 논문 [4]의 그림을 보면 편할 것이다. 노드를 2개부터 5개까지 사용하여 만들 수 있는 모든 겹치지 않는 동형 그래프이다. $G_0$부터 $G_{29}$까지 총 30개가 있다.

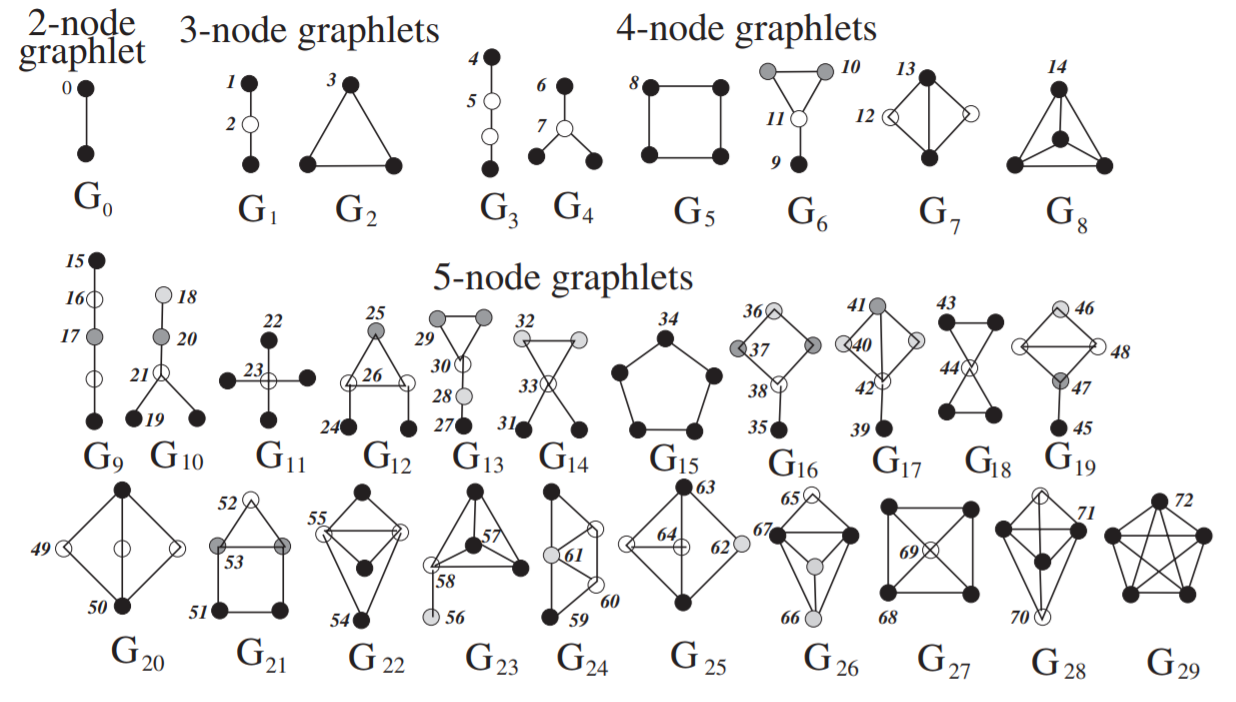
노드 $u$마다 feature 벡터를 만들기 위해서 우리는 $u$에서 만들 수 있는 graphlets의 개수를 종류별로 세서 히스토그램 벡터를 만든다. 이때, 같은 graphlet이더라도 graphlet의 어떤 노드를 $u$와 대응할 것이냐에 따라서 비교 대상이 되는 부분 그래프가 달라질 것이다. 예를 들어, 위 그림 $G_1$의 1번 노드를 $u$에 대응했을 때 만들어지는 부분 그래프와 2번 노드를 $u$에 대응했을 때 만들어지는 부분 그래프가 달라질 것이다. 따라서 노드의 feature 벡터를 만들기 위하여 한 노드에서 고려해야 할 경우의 수가 총 73가지이기 때문에 73차원 벡터가 만들어진다. 이렇게 만든 벡터를 Graphlet Degree Vector (GDV)라고 부른다.

아래 그림은 CS224W [5]에서 등장하는 GDV의 예시이다. 노드 2개와 3개로 만들 수 있는 동형 그래프는 $G_1, G_2, G_3$가 있다. 그래프 $G_3$의 경우, 노드 $c$를 기준으로 하느냐, 노드 $d$를 기준으로 하느냐에 따라서 비교 대상이 되는 부분 그래프가 달라진다. 따라서 비교해야 할 경우의 수는 총 4가지이다. 한편 노드 $c$를 기준으로 하여 비교할 때 조심해야 할 점이 하나 있다. 분명, 노드 $v, u_1, u_2$로 만들어지는 삼각형은 $c$를 기준으로 하는 graphlet을 포함하고 있다. 하지만 노드 $v, u_1, u_2$와 비교할 때는 $v, u_1, u_2$로 만들 수 있는 엣지를 모두 포함하는 부분 그래프와 비교를 해야 한다. 이는 Wikipedia에 있는 graphlets의 정의에서 비롯된 것 같다. 따라서 엣지 $(u_1, u_2)$ 때문에 $c$를 기준으로 한 graphlet과는 일치하지 않는 것이다.

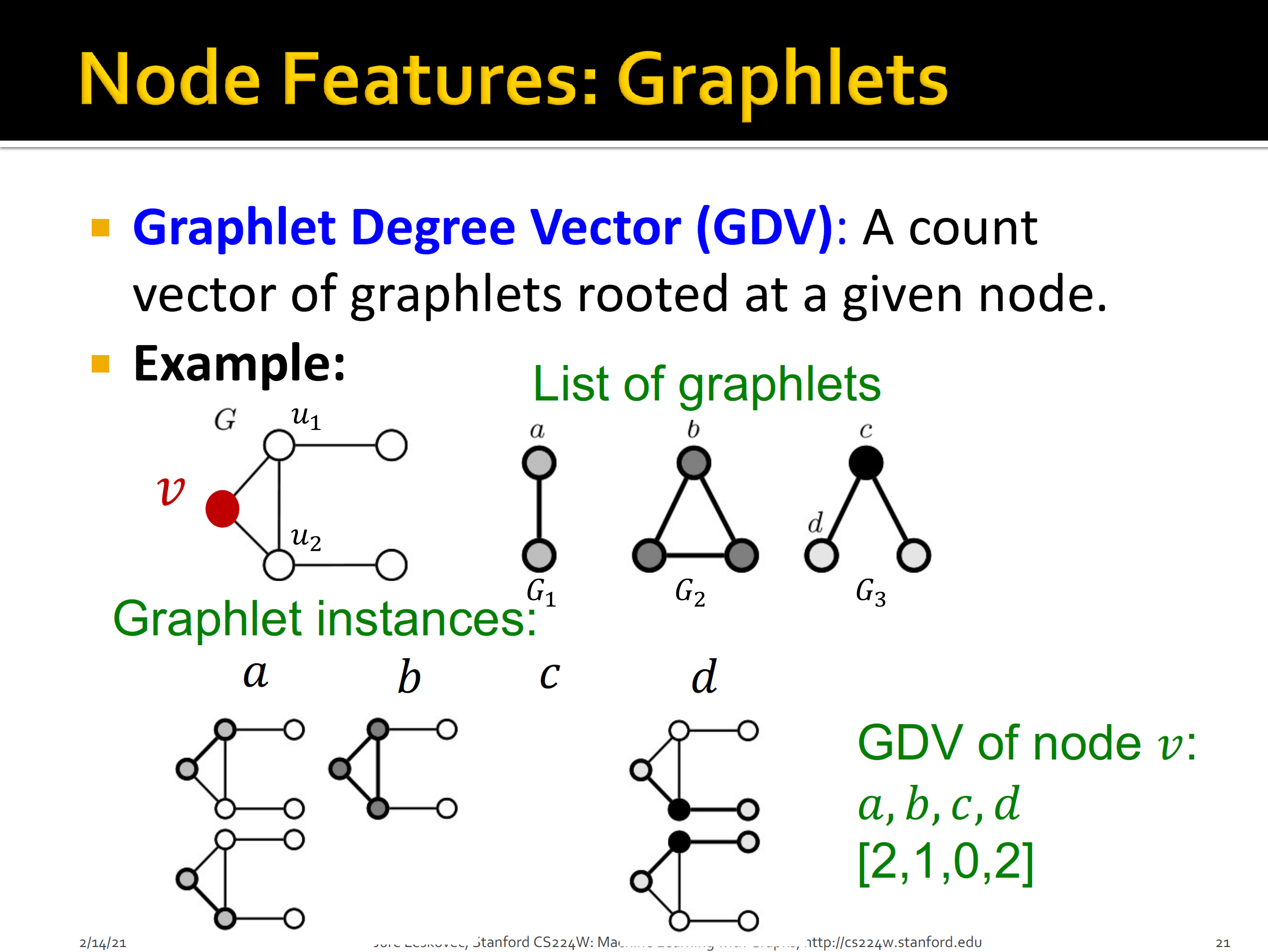
2.1.2 Graph-level Features and Graph Kernels

먼저 이번 섹션에서 빈출하는 개념에 대해 정리하고 가자 !

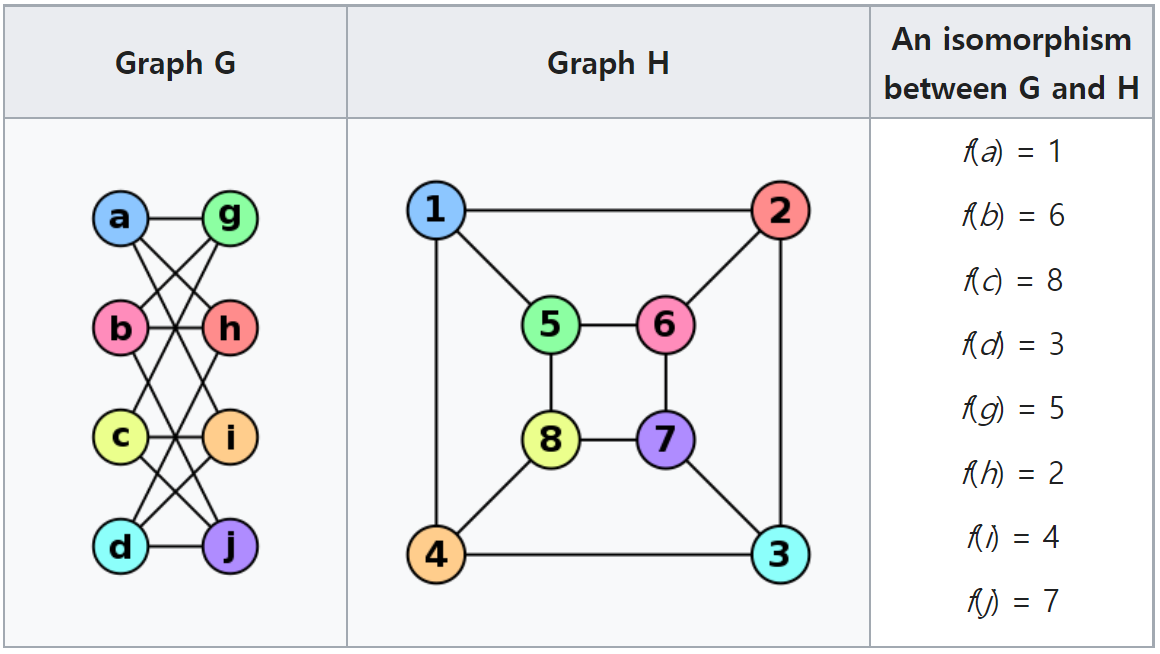
The Weisfeiler-Lehman Kernel

Weisfeiler-Lehman 알고리즘은 두 그래프가 동형인지 아닌지 확인하기 위한 알고리즘이다. 위에서 본 그래프 동형의 정의에 의하면 두 그래프가 동형임을 확인하기 위해서는

• 두 그래프의 노드 집합 사이의 모든 일대일 대응 함수을 하나씩 가져와서
• 일대일 대응 함수에 의해 엣지 정보가 보존되는지 확인해야 했다.

그래프의 노드가 굉장히 많을 경우 가능한 모든 일대일 대응 함수를 탐색하는 것은 현실적으로 불가능한 일이다. Weisfeiler-Lehman 알고리즘은 반복적으로 이웃 노드들의 정보를 취합하는 방식 (iterative neighborhood aggregation)으로 두 그래프가 동형인지 확인할 수 있는 알고리즘이다. 이 알고리즘의 핵심 아이디어는 한 노드의 다음 시점 레이블을 이웃 노드들의 현재 시점 레이블을 취합하여 만드는 것이다. 알고리즘은 다음과 같다.

• 그래프 $G=(V, E)$가 주어졌을 때, 먼저 각 노드 $u \in V$마다 초기 레이블 $c^{(0)}_u$를 부여한다. 일반적으로 $c^{(0)}_u=d_u$로 부여한다.
• $i$번 째 레이블 $c^{(i)}_u$가 주어졌을 때, $i-1$번 째 레이블을 다음과 같이 부여한다.
  • $c^{(i+1)}_u=\text{HASH}(\{ c^{(i)}_u, \{ c^{(i)}_v\}_{v \in \mathcal{N}(v)}\})$
• K번 반복까지 등장한 레이블들에 대한 히스토그램을 그래프의 feature vector로 사용한다.

여기서 집합 괄호 {와 }는 multi-set이다. multi-set은 그냥 집합과는 다르게 원소의 중복을 허용한다. 예를 들어, multi-set은 $\{ 1, 2, 2, 3, 3, 3\}$을 허용한다는 것이다. $\text{HASH}$ 함수는 multi-set으로 표현될 뻔한 레이블에 겹치지 않는 인덱스 (숫자)를 부여해주는 역할을 한다. 요컨데, 한 노드의 다음 시점 레이블을 현재 시점의 이웃 노드들의 레이블을 모아놓은 multi-set으로 표현하고, 다른 레이블들과 겹치지 않는 인덱스를 부여하는 과정을 반복하는 것이다. 예시로 보는 것이 가장 편하다.

예시 그림 coming soon!

Graplets and Path-based method

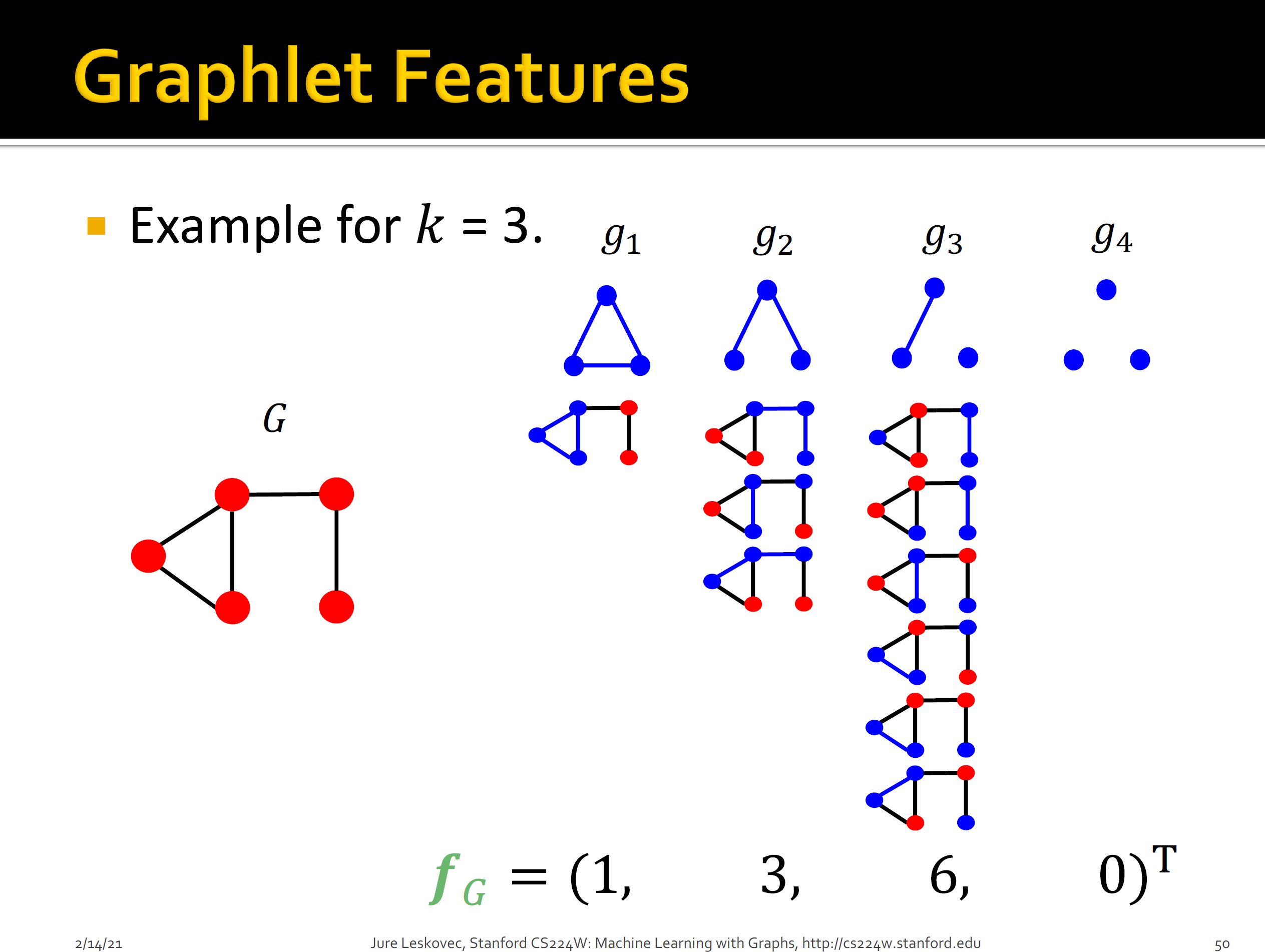
GDV에서는 각 노드에서 만들 수 있는 graphlets의 개수를 세서 히스토그램 벡터를 만들었다. 비슷한 과정을 그래프를 대상으로 할 수 있다. 그래프 안에서 등장하는 graphlets의 개수를 세서 히스토그램 벡터를 만드는 것이다. 하지만 GDV 때와 다른 점이 몇 가지 있다.

• 한 graphlet에서 모든 노드가 연결되어 있을 필요는 없다.
• 기준 노드 개념 없이 비교한다.

아래 그림 역시 CS224W [5]에 나오는 예시이다. 자세한 설명은 생략한다.

이 외에도 그래프 안에서 랜덤 워크를 하고, 서로 다른 경로의 개수를 세서 히스토그램 벡터를 만드는 path-based method들도 있다. 예를 들어, 방문한 노드들의 차수로 수열을 만들고 서로 다른 수열의 개수를 세는 방법이 있다. 물론 랜덤 워크 대신 노드 사이의 최단 경로를 고려하여 벡터를 만들 수도 있다.

2.2 Neighborhood Overlap Detection

섹션 $2.1$ 에서 다뤘던 node-level feature와 graph-level feature로는 두 노드 사이의 유사도는 설명할 수 없다. 예를 들어, 두 노드의 feature 벡터가 유사하다고 해서 두 노드가 그래프 안에서 가까운 것은 아니다. 따라서 이번 장에서는 두 노드 사이의 유사도를 측정할 수 있는 방법들에 대해 알아본다.

특히, 두 노드의 중복된 이웃 노드의 개수를 세서 유사도를 측정하는 이웃 중복도에 대해서 알아볼 것이다. 이웃 중복도 계산의 가장 쉬운 방법은 두 노드가 공유하는 이웃 노드의 개수를 세는 것이다. 즉,

• $\mathbf{S}[u, v]=\mid \mathcal{N}(u) \cap \mathcal{N}(v)\mid \quad \quad (2.7)$

이때, 행렬 $\mathbf{S} \in \mathbb{R}^{\mid V \mid \times \mid V \mid}$는 모든 노드 순서쌍에 대해 유사도를 측정해놓은 행렬로 해석할 수 있다. 이와 같은 행렬 $\mathbf{S}$를 유사도 행렬 (similarity matrix)이라고 부른다. 유사도 행렬은 두 노드 사이의 관계 예측 (relation prediction) 문제에 사용될 수 있다.

2.2.1 Local Overlap Measures

식 $(2.7)$을 기반으로 이웃 중복도를 계산하는 방법들을 local overlap statistic이라고 한다. 하지만 연결된 엣지가 많은 노드의 경우 자연스럽게 식 $(2.7)$의 값이 클 것이다. 따라서 이를 relation prediction에 사용할 경우, 차수가 높은 노드에 대해서는 엣지가 있다고 예측할 확률이 높아질 것이다. 이를 보완하기 위해 다음과 같이 노드 차수로 식 $(2.7)$을 정규하해주는 방법들이 있다.

• $\mathbf{S}_{\text{Sorenson}}[u, v] = \frac{\mid \mathcal{N}(u) \cap \mathcal{N}(v) \mid}{d_u + d_v} \quad \quad (2.9)$
• $\mathbf{S}_{\text{Salton}}[u, v] = \frac{\mid \mathcal{N}(u) \cap \mathcal{N}(v) \mid}{\sqrt{d_ud_v}} \quad \quad (2.10)$
• $\mathbf{S}_{\text{Jaccard}}[u, v] = \frac{\mid \mathcal{N}(u) \cap \mathcal{N}(v) \mid}{\mid \mathcal{N}(u) \cup \mathcal{N}(v) \mid} \quad \quad (2.11) $

한편 두 노드가 공유하는 이웃 노드들의 차수를 고려하는 방법들도 있다. 이 방법들은 두 노드가 공유하는 이웃 노드의 차수가 낮을 수록 더 많은 정보를 주는 엣지라고 가정을 한다.

• Resource allocation index: $\mathbf{S}_{\text{RA}}[v_1, v_2]=\sum\limits_{u \in \mathcal{N}(v_1) \cap \mathcal{N} (v_2)}\frac{1}{d_u} \quad \quad (2.12)$
• Admic-Adar index: $\mathbf{S}_{\text{AA}}[v_1, v_2]=\sum\limits_{u \in \mathcal{N}(v_1) \cap \mathcal{N} (v_2)}\frac{1}{\log d_u} \quad \quad (2.13)$

위의 모든 방법들은 공통된 이웃노드가 없을 경우 두 노드의 local overlap measure가 0이 된다. 하지만 공유하는 이웃 노드가 없다고 해서 두 노드가 그래프 안에서 멀리 위치하라는 법은 없다. 이는 1-hop 이웃 노드들만 고려하여 이웃 중복도를 계산하기 때문에 발생하는 문제점이다.

2.2.2 Global Overlap Measures

섹션 $2.2.1$에서 다뤘던 방법들은 1-hop 이웃만 고려한다는 한계점이 있었다. 이번 섹션에서는 1-hop 이상을 고려하는 방법들에 대해 알아본다.

Katz Index

그래프 $G=(V,E)$ 안의 두 노드 $u, v \in V$의 Katz index는 두 노드를 연결하는 모든 길이의 경로들의 개수를 모두 더한 것이다. 즉,

• $\mathbf{S}_{\text{Katx}}[u,v]=\sum_{l=1}^\infty \beta^l\mathbf{A}^{l}[u,v] \quad \quad (2.14)$

이때, $\beta \in (0, 1]$은 사용자가 설정하는 값이며, 길이가 긴 경로들에 더 낮은 가중치를 부여하는 효과를 갖는다. 그리고 $\mathbf{A}^l[u,v]$는 노드 $u$에서 노드 $v$까지 갈 수 있는 길이 $l$짜리 경로의 개수이다.

행렬 표기도 어지러운데 무한 번 더하라니 정말 너무하다고 느껴진다. 다행히 식 $(2.14)$의 값을 구할 수 있는 공식이 있다고 한다.

• $\mathbf{S}_{\text{Katz}}=(\mathbf{I}-\beta \mathbf{A})^{-1}-\mathbf{I} \quad \quad (2.15)$

식 $(2.15)$에 대한 직관적인 설명은 다음과 같다. 학창시절에 배운 무한 등비급수를 잠시 떠올려보자. $0 \le r < 1$일 때 $\sum_{n=1}^{\infty}r^{n}$의 값은 $\frac{r}{1-r}=\frac{1}{1-r}-1$이었다. 식 $(2.15)$는 무한 등비급수의 행렬판이라고 생각하면 쉽다. $\beta\mathbf{A}$을 $r$으로, $\mathbf{I}$를 $1$으로, 역행렬을 역수로 생각하고 대입하면 정확히 식 $(2.15)$가 나오게 된다. 교재에 보다 더 자세한 증명이 나와있으니 필요한 사람들은 찾아보면 좋을 것 같다.

Katz index는 차수가 높은 노드일 수록 그 값이 커진다는 한계점이 있다. 차수가 높은 노드일 수록 해당 노드로 가능 경로가 많아질 것이기 때문이다.

Leich, Holme, and Newman (LHN) Similarity

위의 한계점을 보완하기 위해서, LHN index는 다음 값을 고려한다.

• $\frac{\mathbf{A}^l[u,v]}{\mathbb{E}[\mathbf{A}^l[u,v]]} \quad \quad (2.16)$

노드 $u$와 $v$를 연결하는 길이 $l$짜리 경로의 개수를 그 기대값으로 나눠서 크기를 제한해주겠다는 것이다. 하지만 우리에게 주어진 그래프 $G$의 인접행렬 $\mathbf{A}$는 딱 하나로 결정될텐데 어떻게 기대값을 취할 수 있는지 의문이 들 것이다.

LHN index에서는 그래프들이 잔뜩 살고 있는 어떤 공간에서 우리의 그래프 $G$가 샘플링되었다고 가정한다. 그 어떤 공간은 그래프 $G$와 동일한 노드와 차수를 갖는 모든 그래프들이 살고 있는 공간이다. 우리는 그 공간에서 랜덤하게 샘플링된 $G$를 우연히 갖고 있는 것이다. 이런 가정 아래에서는 기대값을 취하는 것이 가능하다.

Coming soon!

Random Walk Methods

한편 랜덤 워킹을 사용해서 두 노드 사이의 유사도를 정의하는 방법들도 있다. 한 노드 $u$에서 시작한 랜덤 워크가 어떤 노드 $v$에 많이 방문했다면 두 노드 $u$와 $v$는 유사할 것이라는 가정으로부터 시작된다.

주어진 그래프 $G$의 인접행렬을 $\mathbf{A}$, 각 노드의 차수를 대각 원소로 갖는 대각 행렬을 $\mathbf{D}$라고 하자. $G$의 stochastic 행렬 $\mathbf{P}$는 $\mathbf{P}=\mathbf{A}\mathbf{D}^{-1}$으로 정의된다.

$\mathbf{P}$의 $v$ 번째 열은 $v$의 이웃 노드에 $\frac{1}{d_v}$를 적어준 열벡터이다. 노드 $v$에서 $v$의 이웃 노드들로 이동할 확률로 해석할 수 있다. 반대로 $\mathbf{P}$의 $w$ 번째 행은 $w$의 이웃 노드에서 $w$로 이동할 확률이 적혀 있는 행벡터이다. 따라서 $\mathbf{P}[v_1,v_2]$는 $v_2$에서 $v_1$로 이동할 확률을 나타낸다 ($v_1$에서 $v_2$로 갈 확률이 아님에 유의하자).

노드 $u$에서 시작하여 랜덤 워킹을 $t$번 했을 때, 각 노드에 있을 확률을 나타내는 벡터를 $\mathbf{q}_u^{(t)}$라고 하자. 그럼 $t+1$ 시점에서 각 노드에 있을 확률 벡터 $\mathbf{q}_u^{(t+1)}$는 다음과 같다.

• $\mathbf{q}_u^{(t+1)}=\mathbf{P}\mathbf{q}_u^{(t)}$

$\mathbf{q}_u^{(t+1)}$의 $w$ 번째 원소는 $\mathbf{P}$의 $w$ 번째 행벡터와 $\mathbf{q}_u^{(t)}$를 내적한 것이다. $t+1$ 시점에 $w$에 있을 확률은 ($t$ 시점에 $w$의 이웃 노드에 있을 확률) $\times$ (이웃 노드에서 $w$로 이동할 확률)을 모두 더해준 것이다. 정확히 $\mathbf{P}[w]^T\mathbf{q}_u^{(t)}$ 이다.

랜덤 워킹의 길이가 길어질 수록 $\mathbf{q}_u^{(t)}$는 stationary probability vector $\mathbf{q}_u$로 수렴한다. 이 말은 $\mathbf{q}_u^{(t)} \rightarrow \mathbf{q}_u$ $\text{as}$ $t \rightarrow \infty$ $\text{such that}$

• $\mathbf{q}_u=\mathbf{P}\mathbf{q}_u$

이다. 그리고 $\mathbf{q}_u$는 $\mathbf{P}$의 가장 큰 eigenvalue에 대응하는 eigenvector이다. 이는 정확히 섹션 $2.1.1$에서 다뤘던 eigenvector centrality의 정규화된 벡터이다. 기껏 랜덤 워킹을 도입했는데 eigenvector centrality를 구한 것과 다르지 않다는 것이다. 이건 맛이 없다.

랜덤 워킹에 조미료를 넣어보자. $0$과 $1$사이의 값을 갖는 하이퍼파라미터 $c$를 도입하자. 그리고 $c$의 확률로는 랜덤 워킹을 하고 $1-c$의 확률로는 자기 자신으로 돌아오는 랜덤 워킹을 생각해보자. 이 랜덤 워킹을 다음과 같은 행렬식으로 나타낼 수 있다.

• $\mathbf{q}_u=c\mathbf{P}\mathbf{q}_u+(1-c)\mathbf{e}_u \quad \quad (2.23)$

이때 $\mathbf{e}_u$는 $u$번 째 원소만 $1$이고, 나머지 원소는 $0$인 원핫 벡터이다. 식 $(2.33)$을 정리하면,

• $\mathbf{q}_u=(1-c)(\mathbf{I}-c\mathbf{P})^{-1}\mathbf{e}_u \quad \quad (2.24)$

이다. 최종적으로 random walking similarity는 다음과 같이 정의된다.

• $\mathbf{S}_{\text{RW}}[u,v]=\mathbf{q}_u[v]+\mathbf{q}_v[u] \quad \quad (2.25)$

노드 $u$에서 랜덤워킹을 시작하여 노드 $v$로 방문할 확률과 노드 $v$에서 랜덤워킹을 시작하여 노드 $u$에 방문할 확률을 더한 것으로 이해할 수 있다.

2.3 Neighborhood Reconstrution Methods

2.3.1 Graph Laplacians

Unnormalized Laplacian Matrix

어떤 그래프 $G=(V, E)$의 unnormalized Laplacian 행렬 $\mathbf{L}$ 은 다음과 같이 정의된다.

• $\mathbf{L}=\mathbf{D}-\mathbf{A} \quad \quad (2.26)$

여기서 $\mathbf{A}$는 $G$의 인접행렬을 나타내고, $\mathbf{D}$는 각 노드의 차수를 원소로 갖는 대각행렬이다. Unnormalized Laplacian 행렬은 다음과 같은 성질을 갖는다.

• $\mathbf{L}$은 symmetric 하며, positive semi-definite 하다. 즉, $\mathbf{x}^T \mathbf{L} \mathbf{x} \ge 0 \quad \forall \mathbf{x}\in \mathbb{R}^{\mid V\mid}$
• $\mathbf{L}$의 eigenvalue는 $\mid V \mid$개의 0보다 크거나 같은 eigenvalue를 갖는다.
• 모든 벡터 $\mathbf{x} \in \mathbb{R}^{\mid V \mid}$에 대해서 다음을 만족한다.
  • \[\begin{matrix}\mathbf{x}^T \mathbf{L} \mathbf{x} & = & \frac{1}{2}\sum\limits_{u \in V}\sum\limits_{v \in V}\mathbf{A}[u,v](\mathbf{x}[u] - \mathbf{x}[v])^2 & \quad\quad(2.27) \\ & = & \sum\limits_{(u, v) \in E}(\mathbf{x}[u] - \mathbf{x}[v])^2 & \quad \quad (2.28) \end{matrix}\]
  • 여기서 $\mathbf{A}[u,v]$는 인접행렬 $\mathbf{A}$의 $u$ 행 $v$ 열의 원소를, $\mathbf{x}[u]$는 벡터 $\mathbf{x}$의 노드 $u$번째 원소를 나타낸다.

식 $(2.28)$는 다음과 같이 유도할 수 있다.

• \[\begin{matrix} \mathbf{x}^T \mathbf{L} \mathbf{x} & = & \mathbf{x}^T(\mathbf{D} - \mathbf{A})\mathbf{x} \\ & = & \mathbf{x}^T \mathbf{D} \mathbf{x} - \mathbf{x}^T \mathbf{A} \mathbf{x} \\ & = & \sum\limits_{u \in V}d_u \mathbf{x}[u]^2-\sum\limits_{u \in V}\mathbf{x}[u]\sum\limits_{v \in \mathcal{N}(u)}\mathbf{x}[v] \end{matrix}\]
• 모든 엣지 $(u, v) \in E$에 대하여 왼쪽 시그마에서 $\mathbf{x}[u]^2$과 $\mathbf{x}[v]^2$를 하나씩 꺼내오고, 오른쪽 시그마에서 $\mathbf{x}[u]\mathbf{x}[v]$와 $\mathbf{x}[v]\mathbf{x}[u]$를 하나씩 꺼내오면 $\mathbf{x}[u]^2 -2\mathbf{x}[u]\mathbf{x}[v]+\mathbf{x}[v]^2=(\mathbf{x}[u]-\mathbf{x}[v])^2$을 만들 수 있다.

Normalized Laplacian Matrix

많이 사용되는 normalized Laplacian 행렬 두 가지는 다음과 같다.

• The symmetric normalized Laplacian $\mathbf{L}_{\text{sym}}=\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} \quad \quad (2.32)$
• The random walk Laplacian $\mathbf{L}_{\text{RW}}=\mathbf{D}^{-1}\mathbf{A} \quad \quad (2.33)$

두 라플라시안 행렬은 비슷한 성질들을 갖는다. 스케일 차이 정도만 있다.

2.3.2 Graph Cuts and Clustering

이번 섹션에서는 fully connected 그래프가 주어졌을 때, cut이라는 관점에서 최적의 노드 군집화를 찾는 방법을 알아본다.

Graph cuts

먼저 문제 기술을 위한 용어 및 표기 몇가지를 알아야 한다.

• $G=(V, E)$: 노드 집합 $V$와 엣지 집합 $E$를 갖는 그래프 $G$
• $A \subset V$: 노드 집합의 부분 집합
• $\overline{A} \subset V$: 노드 부분 집합 $A$에 대한 여집합. 즉, $A \cup \overline{A}=V$ 그리고 $A \cap \overline{A}=\emptyset$
• 그래프 partition $\{ A_1, A_2, \cdots, A_K \}$: 그래프 $G$의 노드 집합 $V$을 서로 공통된 원소 없이 를 $K$개의 노드 부분 집합 $A_1, A_2, \cdots, A_K$ 으로 나눈 것. 즉, $\bigcup\limits_{k=1}^{K} A_k = V$ 그리고 $A_i \cap A_j = \emptyset \quad \forall i \ne j$.

그래프 partition의 cut 값은 다음과 같이 정의된다.

• $\text{cut}(A_1,A_2,\cdots,A_K)=\frac{1}{2}\sum\limits_{k=1}^{K}\mid(u,v) \in E : u \in A_k, v \in \overline{A}_k \mid \quad \quad (2.34)$

즉, 두 노드 집합 사이에 연결된 엣지의 개수를 더한 것이다. 하나의 엣지 $(u, v)$는 시그마 안에서 총 두 번 더해지기 때문에 반으로 나눠준 것이다.

따라서 군집의 크기를 고려하면서 cut 값을 최소로 만들어주는 다른 방법들이 고안되었다. Ratio Cut 알고리즘은 다음처럼 군집이 작으면 페널티를 부여한다.

• $\text{RatioCut}(A_1, A_2, \cdots, A_K)=\frac{1}{2}\sum\limits_{k=1}^{K}\frac{\mid(u,v) \in E : u \in A_k, v \in \overline{A}_k \mid}{\mid A_k \mid} \quad \quad (2.35)$

Normalized Cut (NCut)은 군집에 속한 노드들의 차수를 모두 더해준 값으로 cut 값을 나눠준다.

• $\text{NCut}(A_1, A_2, \cdots, A_K)=\frac{1}{2}\sum\limits_{k=1}^{K}\frac{\mid(u,v) \in E : u \in A_k, v \in \overline{A}_k \mid}{\text{vol}(A_k)} \quad \quad (2.36)$

이때, $\text{vol}(A_k)=\sum_{u \in A_k} d_u$ 이다. NCut의 경우 모든 군집들이 비슷한 개수의 엣지를 갖도록 만들어준다.

RatioCut을 사용한 군집화 상세 설명

Cut을 이용한 군집화 알고리즘 이해를 위하여 어떤 그래프 $G$의 노드들을 RatioCut을 사용하여 두 군집으로 나누는 과정을 알아보자. 두 개의 노드 부분 집합을 각각 $A$와 $\overline{A}$라고 표기하겠다. 다음과 같은 벡터를 생각해보자. \(\mathbf{a} \in \mathbb{R}^{\mid V \mid} \quad \text{such that} \quad \mathbf{a}[u]=\begin{cases}\sqrt{\frac{\mid \overline{A} \mid}{\mid A \mid}}, &\quad \text{if $u \in A$} \\ -\sqrt{\frac{\mid A \mid}{\mid \overline{A} \mid}}, & \quad \text{if $u \in \overline{A}$}\end{cases} \quad\quad(2.38)\)

그래프 $G$의 unnormalized Laplacian 행렬 $\mathbf{L}$과 벡터 $\mathbf{a}$를 식 $(2.28)$에 대입해보자. \[\begin{matrix} \mathbf{a}^T \mathbf{L} \mathbf{a} & = & \sum\limits_{(u,v) \in E}(\mathbf{a}[u] - \mathbf{a}[v])^2 & \quad\quad (2.39) \\ & = & \sum\limits_{(u, v) \in E: u \in A, v \in \overline{A}} (\mathbf{a}[u] - \mathbf{a}[v])^2 & \quad\quad (2.40) \\ & = & \sum\limits_{(u, v) \in E: u \in A, v \in \overline{A}}(\sqrt{\frac{\mid \overline{A} \mid}{\mid A \mid}} - (-\sqrt{ \frac{\mid A \mid}{\mid \overline{A} \mid}}))^2 & \quad\quad (2.41) \\ & = & \text{cut}(A, \overline{A})(\frac{\mid \overline{A} \mid}{\mid A \mid} + \frac{\mid A \mid}{\mid \overline{A} \mid} + 2) & \quad\quad(2.42) \\ & = & \text{cut}(A, \overline{A})(\frac{\mid A \mid + \mid \overline{A} \mid}{\mid A \mid} + \frac{\mid A \mid + \mid \overline{A} \mid}{\mid \overline{A} \mid}) & \quad\quad(2.43) \\ & = & \mid V \mid \text{RatioCut}(A, \overline{A}) & \quad\quad(2.44) \end{matrix}\]

• 식 $(2.40)$ : 노드 $u$와 노드 $v$가 둘 다 $A$ 에 속하거나 또는 $\overline{A}$에 속할 경우, $\mathbf{a}[u] = \mathbf{a}[v]$가 돼서 시그마 안의 값이 $0$이 된다. 따라서 시그마의 범위가 $u$와 $v$가 서로 다른 집합에 속한 경우로 축소된다.
• 식 $(2.41)$ : 식 $(2.38)$을 대입한 것이다.
• 식 $(2.42)$ : $(\frac{\mid \overline{A} \mid}{\mid A \mid} + \frac{\mid A \mid}{\mid \overline{A} \mid} + 2)$는 시그마 안의 제곱을 푼 것이다. 그럼 더 이상 $u$와 $v$텀이 없기 때문에 $(\frac{\mid \overline{A} \mid}{\mid A \mid} + \frac{\mid A \mid}{\mid \overline{A} \mid} + 2)$을 $\mid (u,v) \in E : u \in A, v \in \overline{A} \mid$번 곱해준 것이다. 즉, $\text{cut}(A, \overline{A})$번 곱해준 것이다.
• 식 $(2.43)$ : $2= 1+1 = \frac{\mid A \mid}{\mid A \mid} + \frac{\mid \overline{A} \mid}{\mid \overline{A} \mid}$를 대입하고 정리한 것이다.
• 식 $(2.44)$ : 우선, $\mid A \mid + \mid \overline{A} \mid = \mid V \mid$ 와 $\text{RatioCut}(A, \overline{A})=\frac{\text{cut}(A, \overline{A})}{\mid A \mid} + \frac{\text{cut}(A, \overline{A})}{\mid \overline{A} \mid}$을 사용한 것이다.

추가적으로, 식 $(2.38)$에서 정의한 벡터 $\mathbf{a}$는 다음 두 가지 성질을 만족한다.

• $\sum\limits_{u \in V} \mathbf{a}[u] = 0 \iff \mathbf{a} \perp \vec{1} \quad \text{where } \vec{1}=(1,1,\cdots,1)^T \quad\quad(2.45)$

• $\lVert \mathbf{a} \rVert^2=\mid V \mid\quad\quad(2.46)$

• 식 $(2.45)$ : 벡터 $\mathbf{a}$의 정의에 따라 $\mathbf{a}$ 안에는 $\mid A \mid$ 개의 $\sqrt{\frac{\mid \overline{A} \mid}{\mid A \mid}}$ 와 $\mid \overline{A} \mid$개의 $-\sqrt{\frac{\mid A \mid}{\mid \overline{A} \mid}}$가 있다. 각각을 곱해주고 더해주면, $\mid A \mid \sqrt{\frac{\mid \overline{A} \mid}{\mid A \mid}} - \mid \overline{A} \mid \sqrt{\frac{\mid A \mid}{\mid \overline{A} \mid}}=\sqrt{\mid A \mid \mid \overline{A} \mid}-\sqrt{\mid A \mid \mid \overline{A} \mid} = 0$.
• 식 $(2.46)$ : $\lVert \mathbf{a} \rVert^2$ 안에는 $\mid A \mid$ 개의 $\frac{\mid \overline{A} \mid}{\mid A \mid}$ 와 $\mid \overline{A} \mid$개의 $\frac{\mid A \mid}{\mid \overline{A} \mid}$가 있다. 각각을 곱해주고 더해주면, $\mid A \mid \frac{\mid \overline{A} \mid}{\mid A \mid} + \mid \overline{A} \mid \frac{\mid A \mid}{\mid \overline{A} \mid}=\mid A \mid + \mid \overline{A} \mid = \mid V \mid$.

식 $(2.44)$에 의하여 $\mathbf{a}^T \mathbf{L} \mathbf{a} = \mid V \mid \text{RatioCut}(A, \overline{A})$ 이다. 그럼 우리는 RatioCut을 직접 구해서 최소화시킬 필요 없이, $\mathbf{a}^T \mathbf{L} \mathbf{a}$를 최소로 만들어주는 노드 부분 집합 $A$를 찾으면 된다. 즉, \(\operatorname{argmin}_{A \subset V} \mathbf{a}^T \mathbf{L} \mathbf{a} \quad \text{where } \mathbf{a} \text{ defined as in (2.38)}\)

사실 $V$ 의 모든 부분 집합을 고려해야 하기 때문에 NP hard 문제이다. 모든 부분 집합 $A$에 대해서 벡터 $\mathbf{a}$를 만들고 $\mathbf{a}^T \mathbf{L} \mathbf{a}$를 계산해서 크기를 비교해야 한다. “부분 집합 $A$에 대해 최소값을 찾는다.”라는 조건이 너무 강력한 조건이기 때문에 “식 $(2.45)$와 식 $(2.46)$을 만족하는 벡터 $\mathbf{a}$에 대해서 최소값을 찾아주게 된다. \[\operatorname{argmin}_{\mathbf{a} \in \mathbb{R}^{\mid V \mid}}\mathbf{a}^T \mathbf{L} \mathbf{a}\quad \text{s.t } \mathbf{a}\perp\vec{1} \text{ and } \lVert \mathbf{a} \rVert^2=\mid V \mid \quad\quad(2.48)\]

이런류의 최적화 문제가 엄청나게 많다. 어떤 positive semi-definite 행렬 $\mathbf{X} \in \mathbb{R}^{d \times d}$에 대해서 $\max\limits_{\mathbf{v} \in \mathbb{R}^d}\mathbf{v}^T\mathbf{X}\mathbf{v}$ such that $\lVert \mathbf{v} \rVert^2=1$은 $\mathbf{X}$의 가장 큰 eigenvalue에 대응하는 eigenvector $\mathbf{v_1}$에 의해 만들어진다. 그리고 $\max\limits_{\mathbf{v} \in \mathbb{R}^d}\mathbf{v}^T\mathbf{X}\mathbf{v}$ such that $\lVert \mathbf{v} \rVert^2=1$ and $\mathbf{v} \perp \mathbf{v}_1$은 $\mathbf{X}$의 두 번째로 큰 eigenvalue에 대응하는 eigenvector $\mathbf{v}_2$에 의해 만들어진다. 반대로 최소값을 구하는 문제는 가장 작은 eigenvalue에 대응하는 eigenvector를 찾아주면 된다.

책에 증명은 없지만 라플라시안 행렬 $\mathbf{L}$의 가장 작은 eigenvalue에 대응하는 eigenvector가 $\vec{1}$이라고 한다. 따라서 식 (2.48) 최적화 문제는 $\mathbf{L}$의 두 번째로 작은 eigenvalue에 대응하는 eigenvector를 찾아주게 된다. 이렇게 찾은 $\mathbf{a}$의 원소들의 부호에 따라 노드들은 서로 다른 군집으로 할당하게 된다. 즉, \[\begin{cases} u \in A & \quad \text{if } \mathbf{a}[u]\ge0 \\ u \in \overline{A} & \quad \text{if } \mathbf{a}[u]<0 \end{cases}\]

이번 섹션에서는 RatioCut을 이용해서 노드들을 두 군집으로 나누는 방법에 대해 알아봤다. 요컨데, 그래프의 라플라시안 행렬의 두 번째로 작은 eigenvalue에 대응하는 eigenvector를 구하고, 원소의 부호에 따라 노드를 서로 다른 군집에 할당해주었다. 한편, NCut을 사용해서 군집화를 할 경우 $\mathbf{L}_{\text{RW}}$의 두 번째로 작은 eigenvalue에 대응하는 eigenvector를 구하게 된다고 한다.

2.3.3 Generalized Spectral Clustering

섹션 $2.3.2$에서는 라플라시안 행렬 $\mathbf{L}$의 두 번째로 작은 eigenvalue에 대응하는 eigenvector를 찾아서 노드들을 2개 군집으로 나누는 방법을 알아보았다. 이번 섹션에서는 이 개념을 확장해서 노드들을 $K$개의 군집으로 나누는 방법 Generalized Spectral Clustering을 알아보겠다. 방법은 다음과 같다.

1. $\mathbf{L}$의 가장 작은 $K$개의 eigenvalue $0 \le \lambda_1 \le \lambda_2 \le \cdots \le \lambda_K$에 대응하는 eigenvector $\mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_K$를 구한다.
2. 가장 작은 eigenvalue에 대응하는 $\mathbf{e}_1$를 제외하고 $\mathbf{e}_2$부터 $\mathbf{e}_K$ 까지를 열벡터로 갖는 행렬 $\mathbf{U} \in \mathbb{R}^{\mid V \mid \times (K-1)}$를 만든다.

3. 각 행 벡터를 대응하는 노드를 나타내는 벡터 (vector representation 또는 embedding vector 라고 부름)라고 생각하자. 즉 \[\mathbf{z}_u=\mathbf{U}[u] \quad \forall u \in V\]

4. 만든 벡터 representation들에 대해 $K$-means 군집화를 수행한다.

위 방법에서 본 것처럼 우리는 라플라시안 행렬의 spectrum을 사용하여 각각의 노드들을 벡터로 표현할 수도 있다.

• 어떤 행렬의 spectrum은 그 행렬의 eigenvalue을 모아놓은 집합이다.

2.4 Towards Learned Representations

이번 장에서는 노드 또는 그래프로부터 feature를 뽑아서 벡터로 표현하는 방법과 두 노드 사이의 연결을 예측하기 위해서 노드 사이 유사도를 계산하는 방법에 대해서 알아보았다. 그리고 마지막으로 라플라시안 행렬의 eigenvector를 사용하여 노드들을 군집화하는 방법에 대해서도 공부했다. 이 모든 방법은 모두 전문가가 직접 고안한 방법이다. 이는 분명히 진입장벽이 높고, 새로운 방법론을 개발하는데 시간도 많이 걸린다. 따라서 이 책의 다음 챕터부터는 노드, 엣지, 그래프에 대한 벡터 표현법을 학습을 통해 알아내는 Graph Representation Leanring에 대하여 알아볼 것이다.

참고문헌

[1] Hamilton, William L.,Graph Representation Learning, Synthesis Lectures on Artificial Intelligence and Machine Learning, 14, pp.1-159

[2] Graph isomorphism - Wikipedia, https://en.wikipedia.org/wiki/Graph_isomorphism

[3] Graphlets - Wikipedia, https://en.wikipedia.org/w/index.php?title=Graphlets&oldid=1035393985

[4] Nataša Pržulj, Biological network comparison using graphlet degree distribution, Bioinformatics, Volume 23, Issue 2, 15 January 2007, Pages e177–e183, https://doi.org/10.1093/bioinformatics/btl301

[5] CS224W: Machine Learning with Graphs