Chapter 3. Neighborhood Reconstruction Methods

Graph Representation Learning Book 읽고 정리하기 시리즈 중 세 번째 이야기. 부디 완주하게 기도해주세요 !

이번 챕터에서는 노드를 벡터로 표현하는 방법들에 대해서 알아본다. 본격적인 시작에 앞서 이번 챕터에서 자주 마주치게 될 용어들을 알아보고 가자.

노드 임베딩의 목표는 그래프 안의 각 노드를 $d$-차원 벡터로 나타내는 것이다. 이때, 임베딩된 벡터는 그래프 안에서 해당 노드의 위치나 주변 이웃 노드들의 구조를 반영하고 있어야 한다. 조금 더 뜬구름을 잡아보면, latent space에서 두 벡터 사이의 기하적인 관계가 그래프 안에서 대응하는 두 노드 사이의 관계가 될 수 있도록 임베딩 벡터를 만들고 싶은 것이다.

3.1 An Encoder-Decoder Perspective

대부분의 노드 임베딩 알고리즘들은 인코더-디코더 구조를 갖고 있다.

• 인코더는 각 노드를 입력 받아 임베딩 벡터를 출력해주는 역할을 한다.
• 디코더는 임베딩 벡터들을 입력 받아서 그래프 안에서 관심 있는 통계량을 계산해주는 역할을 한다.
  • 예를 들어, 디코더는 2개의 노드 임베딩 벡터를 입력 받아서 두 노드가 그래프 안에서 서로 이웃인지 아닌지를 예측해줄 수도 있다.

이번 섹션에서는 인코더-디코더 구조를 갖는 노드 임베딩 알고리즘의 구성 요소에 대해 알아본다.

3.1.1 The Encoder

그래프 $G=(V, E)$가 있다고 하자. 인코더 $\text{ENC}$는 각 노드 $u \in V$를 입력 받아 $d$-차원 벡터 $\mathbf{z}_u \in \mathbb{R}^d$를 출력해주는 함수이다. 즉,

• $\text{ENC}:V \rightarrow \mathbb{R}^d \; \text{ such that } \; \text{ENC}(u)=\mathbf{z}_u \; \; \forall u \in V\quad \quad (3.1)$

더 정확하게는 노드 $u$를 숫자로 표현할 수 없기 때문에 노드 $u$의 인덱스를 입력 받아서 임베딩 벡터를 출력해준다. (각 노드마다 고유한 숫자를 부여 받은 상황을 가정하기 때문에 노드 $u$를 입력 받는다는 표현도 틀린 표현은 아니다.)

대부분의 노드 임베딩 알고리즘들은 각 노드마다 임베딩 벡터를 모두 구한 후 행렬에 저장해놓는다. 그리고 필요할 때 행렬에서 임베딩 벡터를 꺼내서 사용하는 table-lookup 방식을 택한다. 즉, 각 노드에 대응하는 임베딩 벡터를 행벡터로 갖는 행렬 $\mathbf{Z} \in \mathbb{R}^{\mid V \mid \times d}$이 있을 때, 인코더는 관심 있는 노드 $v$를 입력 받아서 $\mathbf{Z}$의 $v$번 째 행을 출력해준다. 즉,

• $\text{ENC}(v)=\mathbf{Z}[v] \quad \quad (3.2)$

이렇게 노드 임베딩 벡터가 미리 구해진 상황에서 table-lookup 방식으로 노드를 임베딩 하는 방식을 shallow embedding이라고 부른다. 이번 장에서 다룰 대부분의 노드 임베딩 알고리즘은 shallow embedding이다. shallow embedding이 아닌 대표적인 알고리즘으로는 나중에 배울 GNN이 있다고 한다.

3.1.2 The Decoder

디코더는 임베딩 벡터들을 입력 받아서 그래프 안에서 관심 있는 통계량을 복원해주는 역할을 한다. 벡터들을 입력 받아 어떤 숫자를 내뱉는데, 그 숫자가 그래프 안에서의 어떤 통계량과 일치하기를 바라는 것이다. 대부분의 디코더는 두 개의 임베딩 벡터를 입력 받아서 두 노드 사이의 연결성 또는 유사성을 출력해주도록 모델링 된다. 즉,

• $\text{DEC}:\mathbb{R}^{d} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\quad \quad (3.3)$

가장 쉬운 예시로서, 두 개의 임베딩 벡터 $\mathbf{z}_u$와 $\mathbf{z}_v$를 입력 받아서 두 노드 $u$와 $v$가 그래프 안에서 서로 이웃일 확률을 출력해주는 디코더를 생각해볼 수 있다. 좋은 디코더라면

• 두 노드 $u$와 $v$가 그래프 안에서 이웃이 아니라면, $\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=0$을 출력해줄 것이고,
• 두 노드 $u$와 $v$가 그래프 안에서 이웃라면, $\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=1$을 출력해줄 것이다.

따라서 인코더-디코더 구조를 갖는 노드 임베딩의 목표는 다음 식을 만족시키는 것이다.

• $\text{DEC}(\text{ENC}(u),\text{ENC}(v))=\text{DEC}(\mathbf{z}_u, \mathbf{z}_v) \approx \mathbf{S}[u,v] \;\; \forall u, v \in V \quad \quad (3.4)$

여기서 $\mathbf{S} \in \mathbb{R}^{\mid V \mid \times \mid V \mid}$는 노드쌍 $(u, v)$마다 관심 있는 그래프 통계량이 저장된 행렬이다. 주로 그래프 안에서 두 노드 사이의 유사도를 나타내기 떄문에 similarity의 S를 사용한 것 같다. 두 노드 사이의 유사도를 정의하는 가장 쉬운 방법은 서로 이웃하면 유사하다고 정의하는 것이다. 즉, $\mathbf{S}:=\mathbf{A}$이다. 또는, 챕터 $2.2$에서 배운 neighborhood overlap statistic을 사용하여 행렬 $\mathbf{S}$를 만들 수도 있다.

3.1.3 Optimizing an Encoder-Decoder Model

우리는 식 $(3.4)$를 만족시키는 인코더와 디코더를 찾기 위하여 다음과 같은 손실 함수를 정의한다. 그리고 손실 함수를 최소로 만들어주는 인코더와 디코더를 찾게 된다.

• $\mathcal{L}=\sum\limits_{(u, v) \in \mathcal{D}} \mathcal{l} (\text{DEC}(\mathbf{z}_u, \mathbf{z}_v), \mathbf{S}[u,v]), \quad \quad (3.5)$

이때, $\mathcal{l}:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}$ 은 디코더가 예측한 값과 실제 값의 차이를 구해주는 함수이다. $\mathcal{D}$는 훈련 데이터로 사용할 수 있는 노드쌍들의 집합을 나타낸다. 식 $(3.5)$을 최소화시키기 위하여 대부분 노드 임베딩 알고리즘들은 stochastic gradient descent을 택하지만, 일부 알고리즘은 matrix factorization 등의 방법을 사용하기도 한다.

3.1.4 Overview of the Encoder-Decoder Approach

인코더-디코더 구조를 갖는 노드 임베딩은 다음 세 가지를 어떻게 선택하느냐에 따라서 달라질 수 있다. (인코더는 shallow embedding이다. 모든 임베딩 벡터들의 원소가 훈련을 통해 업데이트될 파라미터로 구성된다.)

• 디코더 함수 $\text{DEC}$
• 유사도 행렬 $\mathbf{S}$
• 손실 함수 $\mathcal{l}$

위 세 가지 요소의 선택에 따라서 노드 임베딩 알고리즘 다음과 같이 요약할 수 있다.

이번 장의 나머지 부분에 대해서는 위 알고리즘들을 하나씩 알아본다.

• 섹션 $(3.2)$에서는 matrix factorization 기반의 노드 임베딩 알고리즘에 대해 다뤄본다.
• 섹션 $(3.3)$에서는 비교적 최신 기법인 랜덤 워킹 기반 노드 임베딩 알고리즘에 대해 다뤄본다.

3.2 Factorization-based

Laplacian Eigenmaps

섹션 $3.1$에서 디코더 함수, 손실 함수, 유사도 행렬에 따라서 노드 임베딩 알고리즘을 분류할 수 있다고 했다. 한편 디코더 함수는 두 개의 노드 임베딩 벡터를 입력 받아 그래프 안에서 두 노드 사이의 관계를 출력해주는 함수라고도 했다. 예를 들어, 두 임베딩 벡터 사이의 거리를 디코더 함수로 사용한다면 그래프 안에서 두 노드가 얼마나 다른지에 관심 있는 것이다.

• $\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=\lVert \mathbf{z}_u - \mathbf{z}_v \rVert^2_2 \quad \quad (3.5)$

한편, 행렬 $\mathbf{S} \in \mathbb{R}^{\mid V \mid \times \mid V \mid}$에는 노드쌍 $(u, v)$마다 그래프 안에서의 관계가 저장되어 있다. 주로 두 노드 사이의 유사도가 저장되어 있기 때문에 유사도 행렬이라고도 부른다. 생각해볼 수 있는 가장 쉬운 유사도 행렬은 인접 행렬 $\mathbf{A}$일 것이다. 그래프 안에서 유사한 두 노드에 대해서는 임베딩 공간에서도 가깝게 임베딩시키고 싶다면, 손실함수를 다음과 같이 디자인해야 할 것이다.

• $\mathcal{L}=\sum\limits_{(u, v) \in \mathcal{D}}\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)\cdot \mathbf{S}[u,v] \quad \quad (3.6)$

그래프 안에서 유사한 두 노드는 $\mathbf{S}[u, v]$ 값이 크기 때문에 손실 함수를 최소화시키기 위해서는 $\lVert \mathbf{z}_u - \mathbf{z}_v \rVert^2_2$ 값을 줄여야 할 것이다. 즉, 두 임베딩 벡터를 가깝게 위치시켜야 할 것이다. 한편, 그래프 안에서 관계가 없는 두 노드는 $\mathbf{S}[u, v]$가 0에 가깝다. 따라서 $\lVert \mathbf{z}_u - \mathbf{z}_v \rVert^2_2$ 값을 줄여주지 않아도 괜찮을 것이다.

이때, 유사도 행렬 $\mathbf{S}$를 Laplacian 행렬의 성질을 만족하는 행렬로 사용하면 식 $(3.6)$을 최소화시키는 문제는 섹션 $2.3$에서 다루었던 spectral clustering 문제를 푸는 것과 같아진다고 한다. 즉, $d$-차원 노드 임베딩 벡터을 찾는다고 생각하면, $\min\limits_{\mathbf{Z} \in \mathbb{R}^{\mid V \mid \times d}} \mathcal{L}$의 해는 Laplacian 행렬의 가장 작은 eigenvalue를 제외한 $d$개의 가장 작은 eigenvalue 대응하는 eigenvector를 열벡터로 갖는 행렬이 된다. 위와 같은 세팅으로 노드 임베딩을 하는 알고리즘을 Laplacian eigenmaps라고 부른다고 한다.

한 가지 의문점이 있다. 책에서는 “Laplacian 행렬의 성질을 만족하는 행렬”을 사용해서 식 $(3.6)$을 최소화시킨다고 했다. 그럼 어떤 Laplacian을 사용한다는 것일까? 우리가 배운 Laplacian 행렬은 크게 두 가지가 있다.

• $\mathbf{L}=\mathbf{D}-\mathbf{A}$를 사용할 경우 서로 다른 두 노드쌍 \((u, v)\)의 유사도는 모두 음수가 된다. 그럼 그래프 안에서 가까운 노드를 더 멀리 임베딩시킬 것이다.
• $\mathbf{L}=\mathbf{D}^{-1} \mathbf{A}$를 사용할 경우, $\mathbf{L}$의 모든 원소가 양수이다. 그리고 디코더 함수값도 항상 양수이다. 따라서 손실함수의 lower bound는 0이다. 그리고 모든 노드를 영벡터로 임베딩하면 최소값을 얻을 수 있다.

아마 관련 논문을 직접 읽어봐야 의문점이 해소될 것 같다. 미래의 나 ! 부탁해 !!

Inner-product Methods

한편, 두 노드 임베딩 벡터 사이의 dot product를 디코더 함수로 사용할 수도 있다. 그래프 안에서 두 노드 사이의 유사도가 두 노드 임베딩 벡터의 dot product에 비례할 것이라고 가정하는 것이다.

• $\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=\mathbf{z}_u^T \mathbf{z}_v \quad \quad (3.7)$

그리고 mean-squared error를 손실 함수로 사용할 수도 있다. 즉,

• $\mathcal{L}=\sum\limits_{(u,v) \in \in \mathcal{D}} \lVert \text{DEC}(\mathbf{z}_u, \mathbf{z}_v) - \mathbf{S}[u,v] \rVert^2_2 \quad \quad (3.8)$

이때 유사도 행렬 $\mathbf{S}$로 인접행렬 $\mathbf{A}$를 사용하는 노드 임베딩 알고리즘을 Graph Factorization이라고 부른다. GraRep 노드 임베딩 알고리즘은 인접행렬 $\mathbf{A}$의 거듭제곱꼴 기반의 행렬을 유사도 행렬으로 사용한다. 한편, HOPE 알고리즘에서는 neighborhood overlap measure을 사용해서 유사도 행렬을 만들고 노드 임베딩을 수행하는 일반적인 방법을 제시한다.

위와 같은 방법들을 matrix-factorization 방법이라고 부른다. 각 $d$-차원 노드 임베딩 벡터를 행벡터로 갖는 행렬을 $\mathbf{Z} \in \mathbb{R}^{\mid V \mid \times d}$라고 하자. 식 $(3.8)$의 손실함수를 다음과 같이 행렬 형태로 바꿔서 근사시킬 수 있다.

• $\mathcal{L} \approx \lVert \mathbf{Z} \mathbf{Z}^T - \mathbf{S} \rVert^2_2 \quad \quad (3.9)$

식 $(3.9)$는 모든 노드쌍 $(u,v)$에 대해서 오차가 더해지고, 식 $(3.8)$은 우리가 갖고 있는 엣지 $(u,v)$에 대해서만 오차가 더해진다는 점에서 차이가 있다. 식 $(3.9)$를 최소화한다는 것은 $\mid V \mid \times \mid V \mid$ 크기의 행렬 $\mathbf{S}$를 정보의 손실을 최소화하며 $\mathbf{Z} \mathbf{Z}^T$로 분해한다는 것이다. 이런 관점에서 matrix-factorization 방법이라고 부르는 것이다.

3.3 Random Walk Embeddings

섹션 $3.2$에서 정의했던 유사도 행렬들은 그래프가 주어지면 딱 계산해서 구할 수 있었다. 그래프에 따라 유사도 행렬의 원소들이 딱 정해지기 때문에 deterministic measure 를 사용하여 행렬을 정의했다고 할 수 있다. 한편, 랜덤 워크를 이용해서 유사도 행렬을 정의하는 방법들도 있다. 이 경우 랜덤 워크의 랜덤한 성질 때문에 stochastic measure 를 사용해서 행렬을 정의한다고 말한다. 랜덤 워크 기반 노드 임베딩들은 짧은 길이의 랜덤 워크에서 어떤 두 노드가 동시에 등장할 확률이 높다면 해당 두 노드가 서로 유사하다고 가정한다.

랜덤 워크를 이용한 가장 대표적인 알고리즘으로 DeepWalk와 node2vec이 있다. 이 책에는 두 알고리즘에 대해 아주 간략히 다루고 있다. 따라서 CS224W [3]에서 배운 내용을 정리하려고 한다. 따라서 내용과 표기법이 책과 차이가 있을 수 있다.

DeepWalk

그래프 $\mathcal{G}=(\mathcal{V}, \mathcal{E})$의 두 노드 $u, v \in \mathcal{V}$에 대응하는 $d$-차원 임베딩 벡터를 $\mathbf{z}_u, \mathbf{z}_v \in \mathbb{R}^d$라고 하자. DeepWalk의 디코더는 두 임베딩 벡터의 내적값을 그래프 안에서의 어떤 확률값에 근사시키는 것을 목표로 한다. 즉, \[\mathbf{z}_u^T \mathbf{z}_v \approx P(v \mid \mathbf{z}_u)\]

이때, 확률값은 한 노드에서 랜덤 워킹을 시작했을 때, 다른 노드에 방문할 확률이다. 조건부에는 임베딩 벡터 표기가 있고, 확률 변수에는 노드 표기가 있어서 헷갈릴 수 있다. 이는 하나의 노드 임베딩 벡터 $\mathbf{z}_u$가 주어졌을 때, 노드 $v$가 노드 $u$의 이웃 노드일 확률을 표현하기 위해서이다. 디코더가 벡터들을 입력 받아서 그래프 통계량을 출력한다는 것을 생각하자.

위와 같은 임베딩 벡터를 얻기 위해서 다음과 같은 log-likelihood 목적함수를 정의한다. \[\sum\limits_{u \in \mathcal{V}}\log P(N_R(u) \mid \mathbf{z}_u)=\sum\limits_{u\in \mathcal{V}}\sum_{v \in N_R(u)}\log P(v \mid \mathbf{z}_u) \quad \quad (1)\]

여기서 $N_R(u)$는 랜덤 워킹의 관점에서 노드 $u$와 유사한 노드들을 모아놓은 것이다. 그래서 이를 최대화하면, 노드 $\mathbf{z}_u$가 주어졌을 때 랜덤 워킹의 관점에서 $u$와 유사한 노드들이 확률값을 크게 가져가게 된다.

따라서 노드 $u$의 랜덤 워크 전략 $R$에 대한 이웃 노드 집합 $N_R(u)$를 정의해야 한다. $N_R(u)$는 노드 $u$에서 시작해서 랜덤 워킹을 실시했을 때 방문한 노드들의 multiset이다. 랜덤 워킹 동안 방문한 노드들을 중복 허용해서 모아놓은 집합이다.

식 $(1)$을 최대화한다고 했는데, 무엇에 대해 최대화를 해야 하는가? 우리가 업데이트 시켜나갈 파라미터는 모든 노드 임베딩 벡터 $\mathbf{z}$이다. 처음에는 모든 임베딩 벡터를 임의로 초기화 시켜주고, 식 $(1)$을 커지게 만드는 방향으로 점점 업데이트하게 된다. 이를 위해 조건부확률을 파라미터에 대한 함수로 표현할 수 있어야 한다. 여기서는 softmax를 사용하여 확률 밀도 함수를 모델링한다. 즉, \[P(v \mid \mathbf{z}_u)=\frac{\exp(\mathbf{z}_u^T \mathbf{z}_v)}{\sum\limits_{n \in \mathcal{V}}\exp(\mathbf{z}_u^T \mathbf{z}_n)} \quad\quad (2)\]

식 $(2)$를 식 $(1)$에 대입하면, 우리가 최종적으로 최대화시키고 싶은 대상은 다음과 같다. \[\mathcal{L}=\sum_{u \in \mathcal{V}} \sum_{v \in N_R(u)}\log(\frac{\exp(\mathbf{z}_u^T \mathbf{z}_v)}{\sum\limits_{n \in \mathcal{V}}\exp(\mathbf{z}_u^T \mathbf{z}_n)}) \quad\quad (3)\]

하지만, 노드 수가 굉장히 많은 네트워크에 대해서는 위의 식을 한번 계산하는 것도 굉장히 오래 걸린다. 총 3개의 시그마가 있기 때문이다. 사실 앞에 시그마가 2개는 더하고자 하는 식이 간단하면 큰 문제가 되지 않을 것이다. 하지만 softmax의 분모를 계산하는 것은 굉장히 무거운 계산이다. 따라서 softmax의 분모를 계산할 때 모든 노드 $n \in \mathcal{V}$을 사용하지 않고, 일부 몇 개의 노드만 샘플링해서 더해준 것을 사용한다. 이런 방법을 negative sampling이라고 한다. 즉, \[\log(\frac{\exp(\mathbf{z}_u^T \mathbf{z}_v)}{\sum\limits_{n \in \mathcal{V}}\exp(\mathbf{z}_u^T \mathbf{z}_n)}) \approx \log(\sigma(\mathbf{z}_u^T \mathbf{z}_v)) - \sum_{i=1}^k \log(\sigma(\mathbf{z}_u^T \mathbf{z}_{n_i})), \quad \text{where } n_i \sim P_v \quad (4)\]

여기서 $\sigma(\cdot)$는 시그모이드 함수이다. 식 $(4)$는 솔직히 이해가 잘 되지 않는다. 로그 함수의 성질에 따라서 분자와 분모가 뺄셈으로 분리될 때 로그와 지수함수가 만나면서 $\mathbf{z}_u^T \mathbf{z}_v$만 남을 것 같은데, 왜 굳이 sigmoid를 붙이는지 잘 이해가 되지 않는다. 하지만 논문에서 이렇게 사용했다니 지금 당장은 받아들이고 넘어가겠다.

식 $(4)$에서 노드 $n_i$를 확률 밀도 함수 $P_v$에서 샘플링하게 되는데, $P_v$의 정확한 식은 안 나와 있지만 노드의 차수에 비례하는 확률 밀도 함수라고 한다. 최종적으로 식 $(3)$에 마이너스 부호를 붙이고 gradient descent로 최소화시켜 준다. 이때 softmax의 분모를 계산할 때는 negative sampling을 사용하여 계산량을 줄이게 된다. 최종적인 알고리즘을 뇌지컬로 적어본다면 다음과 같을 것이다.

• 모든 $i$에 대해서 임베딩 벡터 $\mathbf{z}_i$임의 초기화
• 식 (3)이 수렴할 때까지 다음을 반복하시오
  • 모든 $i$에 대해서 노드 $i$에서 시작하는 랜덤워크 $N_R(u)$ 생성
  • 모든 $i$에 대해서 $\frac{\partial\mathcal{L}}{\partial\mathbf{z}_i}$ 계산
  • Gradient ascent (또는 gradient descent) 실시

node2vec

DeepWalk의 설명 중에서 왜 쓰였는지 잘 모르겠는 표현이 있을 것이다. 바로 랜덤 워크 전략 \(R\)이라는 표현이다. 위에서 랜덤 워크를 정의할 때 “이웃 노드 중 한 노드로 임의로 이동”이라는 표현을 사용했는데, 여기에 각 이웃 노드로 이동할 확률이 같다고는 언급한 적이 없다. 모순처럼 들리지만 임의로 이동하는 방법에도 전략이 있을 수 있다. 이 전략에 따라서 랜덤 워크가 달라지고 따라서 \(N_R(u)\)가 달라지게 될 것이다.

생각해볼 수 있는 가장 쉬운 랜덤 워크 전략은 각 이웃 노드로 이동할 확률을 동일하게 부여하는 전략이다. 이 전략을 unbiased 랜덤 워크라고 한다. 어느 방향으로 의도를 가지고 이동하지 않기 때문에 특정 방향으로 편향되지 않는다. DeepWalk가 이에 해당한다.

node2vec은 다른 랜덤 워크 전략을 사용한다. 현재 노드에서 이웃 노드 중 하나를 이동할 때 다음 세 가지 경우 중 하나를 서로 다른 확률로 선택하게 된다.

• 이전 노드로 돌아간다.
• 이전 노드와 현재 노드가 공유하는 이웃 노드 중 하나로 간다. (BFS)
• 이전 노드의 이웃 노드에는 없는 현재 노드의 이웃 노드 중 하나로 간다. (DFS)

아래 그림을 보자. 현재 노드는 $w$이고 이전 노드는 $s_1$이다. 현재 노드에서 다음 노드로 이동하는 경우는 세 가지가 있다고 했다. 첫 번째는 이전 노드 $s_1$으로 돌아가는 것이다. 두 번째는 $s_1$과 $u$의 공동 이웃 $s_2$로 가는 것이다. $s_1$의 이웃들을 먼저 탐색하기 때문에 너비 우선 탐색 (BFS)을 한다고 할 수 있다. 세 번째는 $u$의 이웃이지만 $s_1$의 이웃은 아닌 $s_3$로 가는 것이다. $s_1$의 이웃의 이웃을 탐색하기 때문에 깊이 우선 탐색 (DFS)을 한다고 할 수 있다.

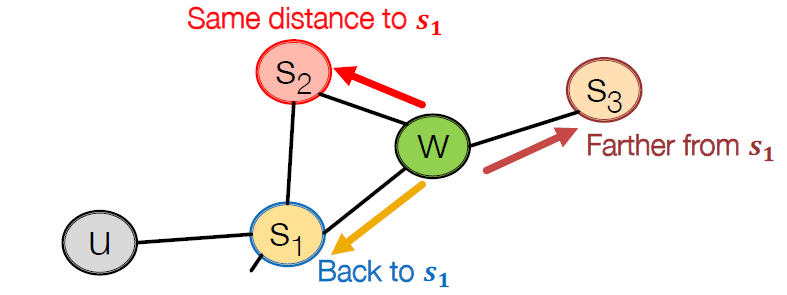
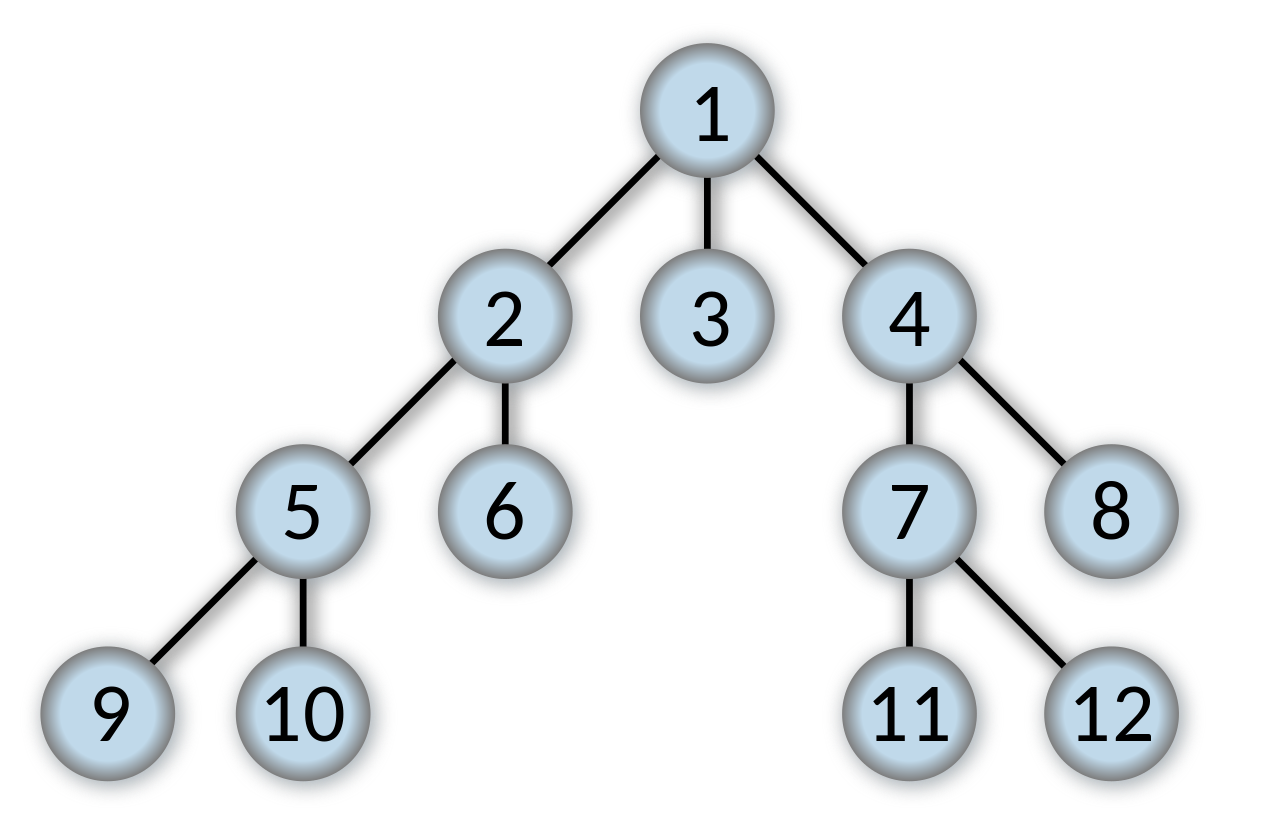
BFS (너비우선탐색, Breath-first search)란 현재 노드로부터 그래프를 탐색할 때 현재 노드들의 이웃 노드들을 먼저 다 탐색하고, 이웃 노드들의 이웃 노드를 탐색하는 방법이다. 아래 그림은 트리 구조 그래프의 루트 노드 ($1$)부터 시작해서 BFS를 할 때, 탐색하는 노드의 순서를 나타낸 것이다.

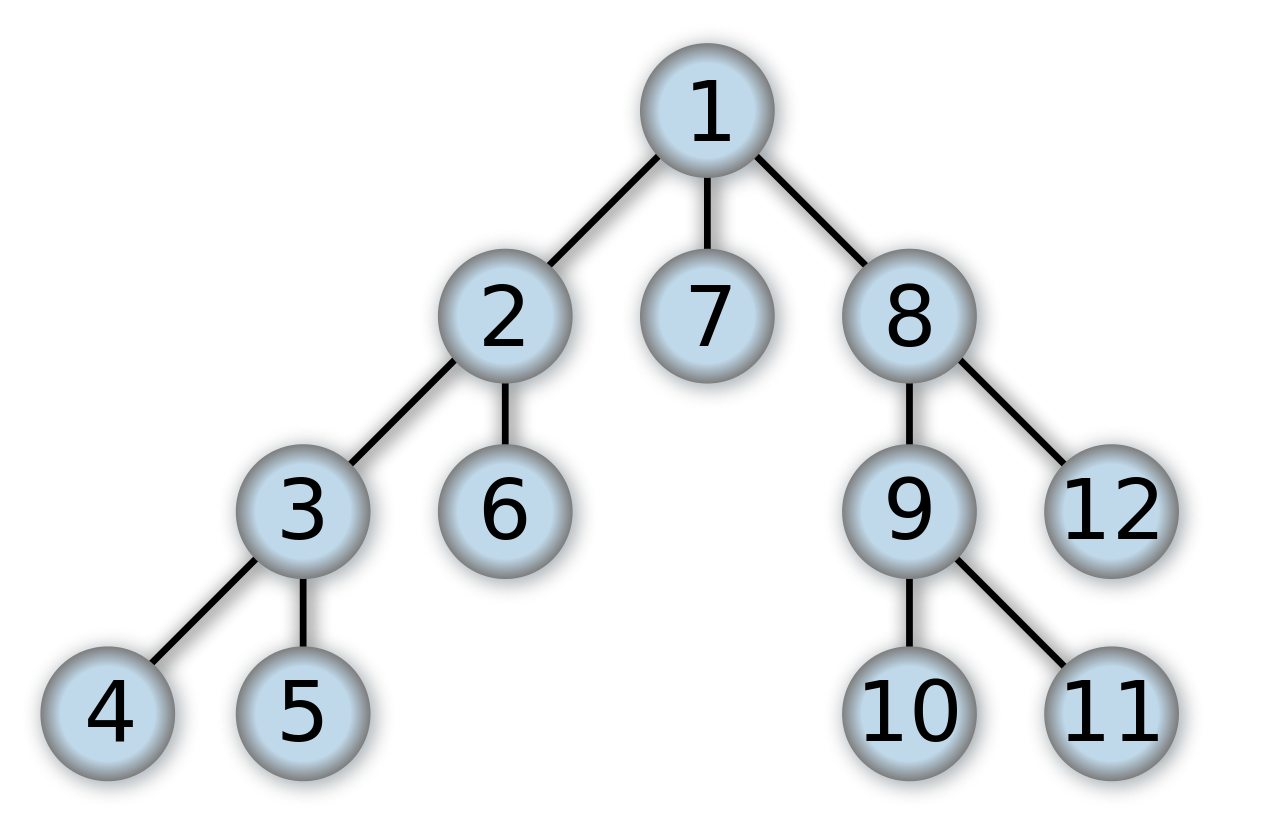
DFS (깊이우선탐색, Depth-first search)는 현재 노드로부터 그래프를 탐색할 때, 이웃 노드 하나를 탐색하고, 그 이웃 노드의 이웃 노드를 탐색하고, 또 그 노드의 이웃 노드를 탐색한 후에 다음 이웃 노드를 탐색하는 방법이다. 아래 그림은 트리 구조 그래프의 루트 노드 ($1$)부터 시작해서 DFS를 할 때, 탐색하는 노드의 순서를 나타낸 것이다.

따라서 node2vec이 취하는 전략은 이전 노드를 기억했다가, 이전 노드로 되돌아가거나, 이전 노드 관점에서 BFS 탐색을 하거나, 이전 노드 관점에서 DFS 탐색을 하는 것으로 이해할 수 있다. BFS 탐색은 한 노드의 이웃 노드 정보를 포착할 수 있고, DFS 탐색은 한 노드로부터 멀리 떨어진 노드 정보를 포착할 수 있다.

node2vec에는 이전 노드로 돌아가는 경우를 선택할 가중치 $p$와 DFS 탐색을 선택할 가중치 $q$를 하이퍼파라미터로 선택할 수 있다. BFS 탐색을 선택할 가중치는 1으로 가중치들의 기준점이 된다. 따라서 한 노드에서 다음 노드로 갈 확률을 그림으로 나타내면 다음과 같다. 아래 그림에서 $\frac{1}{p}, 1, \frac{1}{q}, \frac{1}{q}$의 합이 1이 되도록 정규화를 시켜주고 확률 밀도 함수로 사용하면 된다.

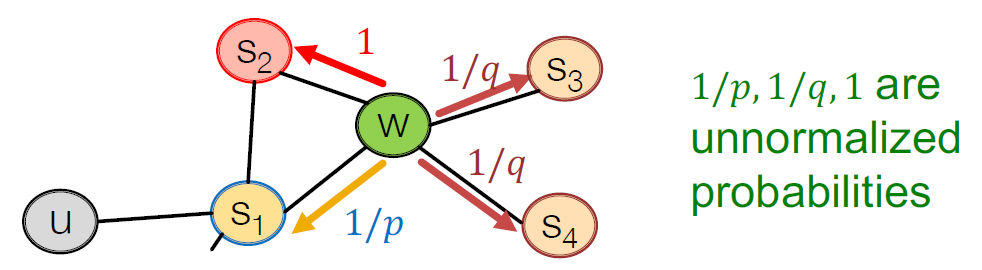
한 노드에서 다음 노드로 이동할 확률 밀도 함수는 노드 임베딩 중 맨 처음에 한번만 구하면 된다. 따라서, node2vec의 과정을 간략히 적어보면,

• 각 노드마다 다음 노드로 이동할 확률 분포 계산
• 각 노드마다 길이 $l$의 랜덤 워크 $r$개씩 생성
• 만들어 놓은 랜덤 워크들로 식 $(3)$ 최적화

Large-scale information network embedding (LINE)

LINE은 DeepWalk와 node2vec과는 다르게 직접적으로 랜덤 워크를 실시하지는 않는다. 하지만 LINE은 두 알고리즘과 비슷한 아이디어를 채택하고 있기 때문에 책에서 간략히 다루고 넘어가고 있다. 지금까지 노드 임베딩들은 하나의 디코더와 하나의 유사도 행렬 $\mathbf{S}$만 사용했다면 LINE은 2개의 목적을 달성하기 위하여 2개의 디코더, 2개의 유사도 행렬을 사용한다.

첫 번째 목적은 인접행렬의 정보를 반영하여 임베딩 벡터를 만드는 것이다. 따라서, 유사도 행렬으로 인접행렬 $\mathbf{A}$를 사용한다. 인접행렬의 각 원소에 근사하기 위한 디코더 함수로는 시그모이드 함수를 사용한다. 즉, \[\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=\frac{1}{1+e^{-\mathbf{z}_u^\top \mathbf{z}_v}} \quad \quad (3.13)\]

두 번째 목적은 2-hop 인접행렬의 정보를 반영하여 임베딩 벡터를 만드는 것이다. 따라서, 유사도 행렬으로 인접행렬의 제곱 $\mathbf{A}^2$을 사용한다. 이 행렬의 각 원소에 근사하기 위한 디코더 함수로는 DeepWalk와 node2vec에서 사용했던 소프트맥스 함수를 사용한다. 즉, \[\text{DEC}(\mathbf{z}_u, \mathbf{z}_v)=\frac{e^{\mathbf{z}_u^\top \mathbf{z}_v}}{\sum_{v_k \in V}e^{\mathbf{z}_u^\top \mathbf{z}_{v_k}}} \quad \quad (3.14)\]

하지만 목적함수로 DeepWalk, node2vec와는 다르게 cross entropy 대신 KL divergence를 사용한다.

Additional variants of the random-walk idea

node2vec에서 보았던 것처럼 랜덤 워크 전략에 따라서 노드 임베딩 결과가 달라질 수 있다. 따라서 랜덤 워크 전략에 대한 다양한 연구가 진행되어 왔다. 책에서 두 가지 논문을 소개하고 있다.

• Perozzi et al [2016]: 랜덤 워크에 skip이란 개념을 추가하여서 GraRep와 비슷한 유사도 행렬을 만들어낸 논문이다. 추측하건데, 이웃 노드로 이동하는 것 뿐만 아니라 2-hop 이웃 노드, 3-hop 이웃노드 등으로 이동을 가능하게 만든 것 같다. 그래서 인접행렬의 거듭제곱꼴 행렬로 만든 유사도 행렬에 근사할 수 있다는 것을 말하고 있는게 아닐까?
• Ribeiro et al [2017]: 한 노드의 이웃 노드 정보보다는 그래프의 구조 관계를 반영하여 임베딩하는 논문이다. 따라서 해당 노드가 그래프 안에서 맡고 있는 구조적인 정보를 반영할 수 있다. 이건 어떤 논문인지 감도 안 온다. 필요한 분들은 읽어볼 것.

3.3.1 Random Walk Methods and Matrix Factorization

이번 섹션도 한 논문을 아주 짧게 리뷰한 것이라고 생각하면 좋다. 논문 이름은 Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec이며 랜덤 워크 기반 노드 임베딩을 모두 matrix factorization으로 해석할 수 있다는 것을 밝힌 논문인 것 같다. 관심 있는 분들께서는 찾아보면 좋을 것 같다.

3.4 Limitations of Shallow Embeddings

이 장의 마지막 섹션인 $3.4$에서는 shallow embedding의 한계점을 짚고 넘어가고 있다.

• 노드 임베딩 벡터들끼리 파라미터를 공유하지 않는다. 즉, 모든 임베딩 벡터들을 하나하나 최적화시켜야 한다. 따라서 우리가 최적화해야 할 파라미터 개수는 $d \times |\mathcal{V}|$개이다. 그럼 파라미터릉 공유하는 노드 임베딩은 무엇이냐? 인코더 함수에 파라미터를 부여해서 인코더를 최적화시키는 것이다. 인코더 파라미터는 모든 노드를 잘 임베딩하는 방향으로 학습되게 된다. 파라미터 수가 적기 때문에 효율적이고, 모든 노드를 잘 임베딩해야 하기 때문에 일반화 성능이 좋을 것이다.
• 노드 feature를 고려하지 않고 임베딩한다. 노드 feature를 갖고 있는 데이터셋이 많은데, 이를 버리고 임베딩하기에는 너무나도 아깝다.
• transductive하다. 이 단어를 네이버에 검색하면 잘 나오지 않는다. 하지만 책의 문맥으로 이해하자면, 훈련에 사용된 노드에 대해서만 노드 임베딩 벡터를 만들 수 있다는 것이다. 즉, 신규 유입되는 테스트 데이터에는 노드 임베딩을 적용할 수 없다는 것이다. 반대 개념으로는 inductive가 있으며 이는 훈련 때 보지 못한 노드에 대해서도 노드 임베딩을 할 수 있는 경우를 말한다.

참고문헌

[1] https://pixabay.com/ko/illustrations/지구-회로망-3537401/

[2] Hamilton, William L.,Graph Representation Learning, Synthesis Lectures on Artificial Intelligence and Machine Learning, 14, pp.1-159

[3] CS224W: Machine Learning with Graphs

[4] Wikipedia - Breadth-first search

[5] Wikipedia - Depth-first search